應(yīng)用型人才培養(yǎng)模式下數(shù)學(xué)建模三級(jí)教學(xué)平臺(tái)的構(gòu)建

孟艷雙+邢育紅

摘要：闡述了應(yīng)用型人才的內(nèi)涵與數(shù)學(xué)建模實(shí)踐活動(dòng)的本質(zhì)，分析了應(yīng)用型人才培養(yǎng)模式下數(shù)學(xué)建模活動(dòng)在人才培養(yǎng)過程中的作用，探討了數(shù)學(xué)建模三級(jí)教學(xué)平臺(tái)的構(gòu)建與實(shí)施。

關(guān)鍵詞：應(yīng)用型人才;數(shù)學(xué)建模;教學(xué)平臺(tái)

中圖分類號(hào)：G642.0 ? ? 文獻(xiàn)標(biāo)志碼：A ? ? 文章編號(hào)：1674-9324（2016）06-0035-03

一、對(duì)應(yīng)用型人才內(nèi)涵與數(shù)學(xué)建模實(shí)踐活動(dòng)的深入認(rèn)識(shí)

應(yīng)用型人才是一種能將專業(yè)知識(shí)和技能應(yīng)用于所從事的專業(yè)社會(huì)實(shí)踐的一種專門的人才類型，是熟練掌握社會(huì)生產(chǎn)或社會(huì)活動(dòng)一線的基礎(chǔ)知識(shí)和基本技能，主要從事一線生產(chǎn)的技術(shù)或?qū)I(yè)人才。在知識(shí)結(jié)構(gòu)上，應(yīng)用型人才更強(qiáng)調(diào)復(fù)合性、應(yīng)用性和與時(shí)俱進(jìn)，具有復(fù)合性和跨學(xué)科的特點(diǎn)。在能力結(jié)構(gòu)上，應(yīng)用型人才強(qiáng)調(diào)發(fā)現(xiàn)問題和解決問題的能力，要求具備解決復(fù)雜問題的實(shí)踐能力;在素質(zhì)結(jié)構(gòu)上，應(yīng)用型人才直接服務(wù)于各行各業(yè)，更強(qiáng)調(diào)社會(huì)適應(yīng)性和與社會(huì)的共處能力。應(yīng)用型人才的特點(diǎn)：強(qiáng)調(diào)實(shí)踐，突出應(yīng)用;終身學(xué)習(xí)，知識(shí)復(fù)合;科學(xué)態(tài)度，敢于創(chuàng)新;責(zé)任意識(shí)，團(tuán)隊(duì)協(xié)作。

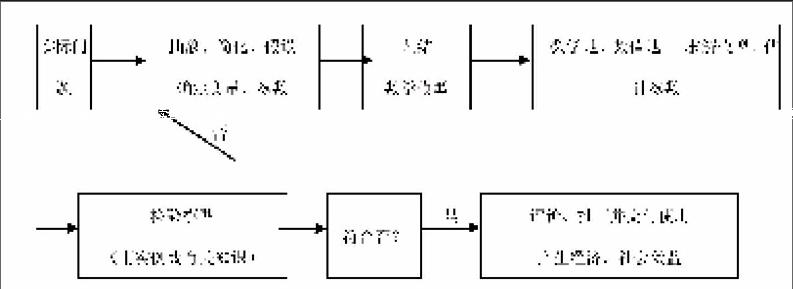
數(shù)學(xué)建模就是通過對(duì)現(xiàn)實(shí)問題的抽象、簡(jiǎn)化，確定變量和參數(shù)，并應(yīng)用某些“規(guī)律”建立起變量、參數(shù)間的確定的數(shù)學(xué)問題;然后求解該數(shù)學(xué)問題，最后在現(xiàn)實(shí)問題中解釋、驗(yàn)證所得到的解的創(chuàng)造過程。數(shù)學(xué)建模過程可用下圖來表明：

因此，數(shù)學(xué)建模活動(dòng)是一個(gè)多次循環(huán)反復(fù)驗(yàn)證的過程，是應(yīng)用數(shù)學(xué)的語言和方法解決實(shí)際問題的過程。數(shù)學(xué)建模是一種聯(lián)系數(shù)學(xué)與實(shí)際問題的橋梁，它突出了實(shí)踐活動(dòng)的重要特點(diǎn)，強(qiáng)調(diào)人才的培養(yǎng)應(yīng)從側(cè)重知識(shí)教育轉(zhuǎn)向側(cè)重應(yīng)用能力培養(yǎng)。

二、應(yīng)用型人才培養(yǎng)模式下數(shù)學(xué)建模活動(dòng)在人才培養(yǎng)過程中的作用

應(yīng)用型人才培養(yǎng)模式下，數(shù)學(xué)建模活動(dòng)不僅包括學(xué)習(xí)數(shù)學(xué)知識(shí)，展示各應(yīng)用領(lǐng)域中的數(shù)學(xué)問題和建模方法，提高學(xué)生學(xué)習(xí)數(shù)學(xué)的積極性，更重要的是培養(yǎng)學(xué)生應(yīng)用數(shù)學(xué)知識(shí)解決實(shí)際問題的能力，創(chuàng)造有利于提高學(xué)生將來從事實(shí)際工作能力的環(huán)境。數(shù)學(xué)建模活動(dòng)的教學(xué)內(nèi)容和教學(xué)方法是以應(yīng)用型人才培養(yǎng)為核心，內(nèi)容取材于實(shí)際、方法結(jié)合于實(shí)際、結(jié)果應(yīng)用于實(shí)際，對(duì)學(xué)生能力的培養(yǎng)體現(xiàn)在多個(gè)方面。

（一）培養(yǎng)學(xué)生分析問題與解決問題的能力

數(shù)學(xué)建模競(jìng)賽的題目一般由工程技術(shù)、經(jīng)濟(jì)管理、社會(huì)生活等領(lǐng)域中的實(shí)際問題簡(jiǎn)化而成，在數(shù)學(xué)建模活動(dòng)中，要求首先強(qiáng)調(diào)如何分析實(shí)際問題，如何利用所掌握的知識(shí)和對(duì)問題的理解提出合理且簡(jiǎn)化的假設(shè)，如何將實(shí)際問題抽象為數(shù)學(xué)問題，即將實(shí)際問題“翻譯”成數(shù)學(xué)模型。其次是如何建立適當(dāng)?shù)臄?shù)學(xué)模型，如何利用恰當(dāng)?shù)姆椒ㄇ蠼鈹?shù)學(xué)模型，以及如何利用模型結(jié)果解決實(shí)際問題。對(duì)數(shù)學(xué)模型求解后，還要用數(shù)學(xué)模型的結(jié)果解釋實(shí)際現(xiàn)象。這是一個(gè)雙向“翻譯”的過程，通過這個(gè)過程，讓學(xué)生體驗(yàn)數(shù)學(xué)在解決實(shí)際問題中的作用，培養(yǎng)學(xué)生應(yīng)用數(shù)學(xué)知識(shí)的意識(shí)和能力，從而提高學(xué)習(xí)數(shù)學(xué)的興趣和應(yīng)用數(shù)學(xué)解決實(shí)際問題的能力。數(shù)學(xué)建模本身就是一個(gè)創(chuàng)新的過程并且為培養(yǎng)學(xué)生創(chuàng)新精神和創(chuàng)造能力提供了環(huán)境。

（二）培養(yǎng)學(xué)生的創(chuàng)造精神和創(chuàng)新能力

創(chuàng)造精神和創(chuàng)新能力是指利用自己已有的知識(shí)和經(jīng)驗(yàn)，在個(gè)性品質(zhì)支持下，新穎而獨(dú)特地提出問題、解決問題，并由此產(chǎn)生有價(jià)值的新思想、新方法、新成果。數(shù)學(xué)建模問題的解決沒有標(biāo)準(zhǔn)答案、不局限于唯一方法，不同的假設(shè)就會(huì)產(chǎn)生不同的模型，同一類模型也會(huì)有很多不同的數(shù)學(xué)求解方法。數(shù)學(xué)建模的每一步都給學(xué)生留有較大的空間，在數(shù)學(xué)建模活動(dòng)中，要鼓勵(lì)學(xué)生勤于思考、大膽實(shí)踐，不拘泥于用一種方法解決問題，嘗試運(yùn)用多種數(shù)學(xué)方法描述實(shí)際問題，鼓勵(lì)學(xué)生充分發(fā)揮想象力、勇于創(chuàng)造新方法，不斷地修改和完善模型，不斷地積累經(jīng)驗(yàn)，逐步提高學(xué)生創(chuàng)新能力，數(shù)學(xué)建模本身就是一個(gè)創(chuàng)新的過程并且為培養(yǎng)學(xué)生創(chuàng)新精神和創(chuàng)造能力提供了環(huán)境。數(shù)學(xué)建模是培養(yǎng)學(xué)生創(chuàng)造性思維和創(chuàng)新精神的良好平臺(tái)。

（三）培養(yǎng)學(xué)生的學(xué)習(xí)探索能力

心理學(xué)家布魯納指出：探索是數(shù)學(xué)教學(xué)的生命線。培養(yǎng)學(xué)生的探索能力，應(yīng)貫串?dāng)?shù)學(xué)教學(xué)的全過程。這一點(diǎn)在普通的數(shù)學(xué)課堂上往往做不到。但在數(shù)學(xué)建模的教學(xué)過程中，通常會(huì)有意識(shí)地創(chuàng)設(shè)探索情境，引導(dǎo)學(xué)生以自我為主，進(jìn)行調(diào)查研究、查閱文獻(xiàn)、制定方案、設(shè)計(jì)實(shí)驗(yàn)、構(gòu)思模型、分析總結(jié)等方面獨(dú)立探索能力的訓(xùn)練，促進(jìn)學(xué)生創(chuàng)新精神、科研能力和實(shí)踐技能的培養(yǎng)。

（四）培養(yǎng)學(xué)生的洞察力和抽象概括能力

數(shù)學(xué)建模的模型假設(shè)需要根據(jù)對(duì)實(shí)際問題的觀察和分析，透過現(xiàn)象看本質(zhì)，將錯(cuò)綜復(fù)雜的實(shí)際問題簡(jiǎn)化，再進(jìn)行高度的概括，抽象出合理、簡(jiǎn)化、可行的假設(shè)條件。數(shù)學(xué)建模促進(jìn)了對(duì)學(xué)生的洞察力和抽象概括能力的培養(yǎng)。

（五）培養(yǎng)學(xué)生利用計(jì)算機(jī)解決實(shí)際問題的能力

在數(shù)學(xué)建模中，很多模型的求解都面臨著復(fù)雜的數(shù)學(xué)推導(dǎo)及大量的數(shù)值計(jì)算，同時(shí)所建模型是否與實(shí)際問題相吻合也常常需要通過計(jì)算或模擬來檢驗(yàn)，能熟練使用計(jì)算機(jī)計(jì)算數(shù)學(xué)問題是對(duì)學(xué)生的必要要求。數(shù)學(xué)建模將數(shù)學(xué)、計(jì)算機(jī)有機(jī)地結(jié)合起來，逐步培養(yǎng)學(xué)生利用數(shù)學(xué)軟件和計(jì)算機(jī)解決實(shí)際問題的能力。

（六）培養(yǎng)學(xué)生論文寫作和語言表達(dá)的能力

數(shù)學(xué)建模的考核內(nèi)容一般包括基本建模方法的掌握、簡(jiǎn)單建模問題的求解和實(shí)際問題的解決，考核方式往往采取閉卷與開卷相結(jié)合、理論答卷與上機(jī)實(shí)驗(yàn)相結(jié)合、筆試與答辯相結(jié)合的方法。因此，數(shù)學(xué)建模答卷需要學(xué)生具有一定的描述問題的能力、組織結(jié)構(gòu)的能力以及文字表達(dá)的能力。而數(shù)學(xué)建模競(jìng)賽成績(jī)的好壞、獎(jiǎng)項(xiàng)的高低，其評(píng)定的唯一依據(jù)就是數(shù)學(xué)建模論文，假設(shè)是否合理，建模方法是否有特色，重點(diǎn)是否突出，模型結(jié)果是否正確，論文撰寫是否清晰等是對(duì)論文成績(jī)?cè)u(píng)定的主要標(biāo)準(zhǔn)。通過數(shù)學(xué)建模確實(shí)能培養(yǎng)學(xué)生的論文寫作能力和語言表達(dá)能力。

（七）培養(yǎng)學(xué)生的交流與合作能力和團(tuán)隊(duì)精神

數(shù)學(xué)建模中的實(shí)際問題涉及多個(gè)學(xué)科領(lǐng)域，所需知識(shí)較多，因此集體討論、學(xué)生報(bào)告、教師點(diǎn)評(píng)是經(jīng)常采用的教學(xué)方式。數(shù)學(xué)建模競(jìng)賽活動(dòng)是一個(gè)集體項(xiàng)目，比賽要求參賽隊(duì)在3天之內(nèi)對(duì)所給的問題提出一個(gè)較為完整的解決方案，具有一定規(guī)模的建模問題一般都不可能由個(gè)人獨(dú)立完成，這就需要三個(gè)人積極配合，協(xié)同作戰(zhàn)，要發(fā)揮每個(gè)人的長(zhǎng)處，互相彌補(bǔ)短處，是培養(yǎng)學(xué)生全局意識(shí)、角色意識(shí)、合作意識(shí)的過程，也是一個(gè)塑造學(xué)生良好個(gè)性的過程。在此過程中，既要發(fā)揮好學(xué)生各自特點(diǎn)，又要有及時(shí)妥協(xié)的能力，目的是發(fā)揮整體的最好實(shí)力。作為對(duì)學(xué)生的一種綜合訓(xùn)練，除了三個(gè)人都要有數(shù)學(xué)建模的基礎(chǔ)知識(shí)外，成員之間的討論、修改、綜合，既有分工，又有合作。只有充分的團(tuán)隊(duì)合作，才能取得成功，凡是參加過競(jìng)賽的每一個(gè)人都能深刻體會(huì)到這種團(tuán)隊(duì)精神的重要性，認(rèn)識(shí)到這一點(diǎn)對(duì)學(xué)生以后的成長(zhǎng)是非常有幫助的。