談數學直覺思維的培養策略

張磊

（韓山師范學院數學與統計學院，廣東潮州 521041）

談數學直覺思維的培養策略

張磊

（韓山師范學院數學與統計學院，廣東潮州 521041）

數學直覺思維是以一定的知識經驗為基礎，通過對數學對象的結構及其關系作整體觀察，在一瞬間領悟到對象的某方面的本質，從而迅速做出判斷的一種認知能力.學生一旦有了某個知識的數學直覺，就可加深對該知識的理解，既提升了學生的形象思維，又對抽象思維予以支撐，有利于認清數學本質.在具體的數學教學中，要通過創設數學實驗、增強直覺感知，展示實物模型、提升直覺能力，尋找數學原型、加深直覺認識，借助聯想思維、拓展直覺深度等策略，來培養中學生的數學直覺思維能力.

中學生；數學直覺；培養；策略

筆者常常聽到一些中學數學教師抱怨：學生缺乏數學直覺，培養學生的數學直覺能力非常困難.經常會遇到許多學生對做題的結果缺乏基本的直覺認識，比如在求sina值時，有學生計算出值為2，就作為答案照寫不誤；再如求橢圓離心率時，有學生算出結果為 2，也不假思索地作為答案.如果單純地問這些學生：sina與橢圓離心率的范圍是多少？他們會毫不猶豫地回答：[-1,1]和（0,1）.那為何學生明明知道這些知識點，而在做題時卻寫出不在這個結論范圍之內的答案呢？筆者認為原因是多方面的，但有一點不可否認，那就是學生只簡單地記住了表面上的結論，而沒有去深刻理解這個結論，也沒有納入到自己已有的認知結構中去，于是導致做題得出的結果與記住的結論孤立開來，沒有整合為一個整體，變成了“兩張皮”.說到底，現在的中學生缺少數學直覺.

1 對數學直覺的認識

一般認為，數學直覺思維是以一定的知識經驗為基礎，通過對數學對象（結構及其關系）作整體觀察，在一瞬間領悟到對象的某方面的本質，從而迅速做出判斷的一種認知能力.它憑借已有的經驗知識信息，不受某種邏輯規則的約束，但受邏輯規則的指導，通過想象、猜測以及高速高效的對比、分析、轉換、綜合等，對事物作出直接的估斷或預見[1-3].直覺思維可分為想象型和靈感型，想象型是一般的直覺思維形式，靈感型表現為人們對長期探索而未解決問題的一種突然性領悟，也就是對問題百思不得其解時的一種“茅塞頓開”[4].因而數學直覺思維具有非邏輯性、創造性、突發性、偶然性、或然性、經驗性等[5-6].但從培養數學直覺思維能力的角度來看，筆者認為它具有以下幾個特點：

1.1 非邏輯性

直覺思維的非邏輯性，是它的本質特性.直覺思維并不是根據一定的規律按部就班地進行的，它不是歸納式的概括也不是演繹式的推理，同分析和綜合邏輯方法也不一樣，它是依靠思維中的想象、猜測和測察力等非邏輯功能去直接地把握對象的[7].它并不遵循固定的邏輯規則，相反的，它有意或無意地打破固定的不變的邏輯規則的束縛，在非邏輯方面另辟蹊徑.當然這并不意味直覺思維排斥邏輯思維，事實上，邏輯思維對直覺思維具有誘導作用，在直覺思維中有時要借助于邏輯思維的方法.

1.2 創造性

現代社會需要創造性的人才，我國的教材由于長期以來借鑒國外的經驗，過多的注重培養邏輯思維，培養的人才大多數習慣于按部就班、墨守成規，缺乏創造能力和開拓精神.直覺思維是基于研究對象整體上的把握，不專意于細節的推敲，是思維的大手筆.正是由于思維的無意識性，它的想象才是豐富的，發散的，使人的認知結構向外無限擴展，因而具有反常規律的獨創性[8].因此，直覺思維能產生新的認識和發現，真正可貴的因素是直覺，愛因斯坦說，科學原理雖然是以直接經驗為基礎，但是原理的發現，并沒有邏輯的道路，只有通過那種以對經驗的共鳴的理解為依據的直覺.

1.3 簡約性

直覺思維是對思維對象從整體上考察，調動自己的全部知識經驗，通過豐富的想象作出的敏銳而迅速的假設、猜想或判斷，它省去了一步一步分析推理的中間環節，而采取了“跳躍式”的形式[9].它是一瞬間的思維火花，是長期積累上的一種升華，是思維者的靈感和頓悟，是思維過程的高度簡化，但是它卻清晰的觸及到事物的“本質”.

1.4 自信力

學生對數學產生興趣的原因有兩種，一種是教師的人格魅力，其二是來自數學本身的魅力[10].不可否認情感的重要作用，但筆者的觀點是，興趣更多來自數學本身.成功可以培養一個人的自信，直覺發現伴隨著很強的“自信心”.相比其它的物質獎勵和情感激勵，這種自信更穩定、更持久.當一個問題不用通過邏輯證明的形式而是通過自己的直覺獲得，那么成功帶給他的震撼是巨大的，內心將會產生一種強大的學習鉆研動力，從而更加相信自己的能力[11].高斯在小學時就能解決問題“1+2+ 3+…+99+100=？”，這是基于他對數的敏感性的超常把握，這對他一生的成功產生了不可磨滅的影響.而現在的中學生極少具有直覺思維，對有限的直覺也半信半疑，不能從整體上駕馭問題，也就無法形成自信.

2 數學直覺的培養意義

“數學王子”高斯曾經反復強調，他的數學發現主要來自經驗，“證明只是補行的手續”.德國數學家伊恩·斯圖加特也說：“直覺是真正的數學家賴以生存的東西”.美籍匈牙利數學家波利亞也曾說過：“直觀的洞察和邏輯的證明是感知真理的兩種不同方式——直觀的洞察可能遠遠超前于形式邏輯的證明.”[12]縱觀人類科技進步發展史，許多重大的發現都是基于直覺：歐幾里得幾何學的五個公式就是基于直覺，從而建立起歐幾里得幾何學這棟輝煌的大廈；哈密頓是在散步的路上迸發出了構造四元素的火花；阿基米德在浴室里找到了辨別王冠真假的方法；凱庫勒發現苯分子環狀結構更是一個直覺思維的成功典范.

認知心理學家認為學生學習數學新知的過程，就是一個自我建構的過程，人的大腦會根據已有的認知基礎，對新知進行加工和重新組合，以形成一個新的結構體系，而要熟知這個新結構，就必須要對剛納入的新知有一個直覺的認識，這就需要學生通過自己的親身體驗和領悟才會有直觀的感覺，留下的印象也更加深刻，可能還會體驗到成功的喜悅，從而更能激發起對數學學習的興趣.

所以，學生一旦在腦中有了某個知識的數學直覺，不僅可加深學生對此知識的理解，特別是某些抽象性強、難于理解的概念、法則與結論等，還可增強學生的形象思維，并對抽象思維予以支撐.當然，最直接的好處便是解題時學生有了直覺思維，可以更簡單便捷地認識到題目的本質，這就是培養數學直覺的意義所在.當然這種數學直覺能力需要教師的有意識培養，比如可通過一些具體圖形、模型或生活中的數學現實等，以提升直覺能力.

3 數學直覺的培養策略

新課程標準指出：“學生的數學學習活動不應只限于接受、記憶、模仿和練習，高中數學課程還應倡導自主探究、動手實踐、合作交流、閱讀自學等學習數學的方式.”[13]因此從新課程實施的這幾年來，工作在第一線的數學教師也基本上接受了這些新的教學理念.比如對于概念、定理、公式等的新授課都能安排局部探究和小組合作，盡量在課堂上調動學生的積極性和發揮學生的主觀能動性，并能將學生合作與獨立思考綜合起來運用.當然，除此之外，還可以動手實踐、直觀感知、操作確認等學習方法，這給數學直覺的培養方式指明了方向.筆者結合這幾年在中學的聽課經歷，談談培養數學直覺的一些策略.

3.1 策略一：創設數學實驗，增強直覺感知

當學生難以發現所學知識結論和相互間的關系或規律時，可通過創設數學實驗，讓學生進行動手操作實踐，以體驗數學發現的過程，增強對所學知識的直覺感知.

那何謂數學實驗呢？筆者認為數學實驗就是實驗者借助于一些道具或儀器，通過自己動手進行親自感受與體驗，并在一定思維活動下得出的規律和結論或者驗證了某項猜想和理論的探究活動.當然，這些數學實驗除了動手操作外還一定要有思維活動的參與.

現在許多有條件的中學都在使用圖形計算器，并把它作為一項數學實驗來操作.筆者不反對這種形式的數學實驗，但以現在我國的教學現狀來看，絕大多數學校還不具有這樣的裝備，如果讓學生自備更不現實.所以本文提到的數學實驗更有點類似于物理或化學形式的實驗，道具或儀器可以自己簡易制作.

正因為數學實驗是通過學生自己的操作實踐，所以可形成最初的直觀感知，繼而通過思考想象，再到發現、歸納、猜想，使學生親歷數學知識的建構過程，便于發現數學規律，增強數學直覺.

案例1讓橢圓“圓”形畢露

在《橢圓》的第1課時教學中，大多數高中數學教師采用的基本流程是：教師先用繩子畫橢圓，再歸納出橢圓定義，然后建立橢圓方程，教師講解例題與練習.筆者發現在這個按照教材編寫的順序進行教學時，學生總有一種莫名其妙的感覺：那就是所學的橢圓與圓毫無關系.可既然無關系，為什么“橢圓”中有個“圓”字呢？因此學生心目中的“橢圓”應該會與圓有一定的聯系，至少它們外表“相近”，即是“橢”的圓.由于“橢圓”給人的感覺是一個長圓形，是由圓“壓扁”或“伸長”而成的，那教師為什么不提圓呢？所以，學生心中覺得這個橢圓純粹是“空降”而來，既沒有人情味也感到不合常理，從而產生一種不自然感，也降低了學生對橢圓的直覺認識.為此，筆者認為在引入上不妨進行實驗改進.

引入時的實驗可這樣設計：先讓同桌倆同學合作，用一條細繩子在紙上按住兩端點畫出橢圓，然后讓同學探究：當兩端點離得越來越近和越來越遠時橢圓的形狀變化.

通過學生的實驗操作，就會發現：當兩端點越來越近時，畫出的橢圓越來越圓，當兩端點重合時就變成了圓；而當兩端點離得越來越遠時，畫出的橢圓就越扁.這樣學生就會自己研究出橢圓與圓的關系，從而對橢圓的得出不會感到突然，也增強了對橢圓的直觀認識，同時還為橢圓離心率的大小影響橢圓形狀的知識埋下了伏筆：當橢圓越圓，e就越小，當e=0時就變了圓；橢圓越扁，e越大，當e→a時，e→1.有了這樣的動手實驗，學生對圓與橢圓的形狀及e的范圍在（0,1）有了直觀感受，而腦中有了這樣的直覺感知，也就不會出現當e=2時還作為橢圓離心率答案的錯誤現象，因為學生通過自己的實驗操作而產生的印象遠比老師空洞說教要深刻得多.

3.2 策略二：展示實物模型，提升直覺能力

在講授一個新的數學知識，尤其是抽象性比較強、學生一時難以理解或不能想象的數學知識時，就要聯系學生生活中可見到的實物，以幫助學生理解，增加直觀性.筆者認為教師通過實物模型的展示是培養學生數學直覺的一個不錯選擇.因為具體的實物模型可以降低抽象難度，提升直觀形象.特別是在講授立體幾何知識時，更需要用實物模型來直觀認知，再通過實驗操作來確認，這樣才能消除學生初中所學的平面幾何帶來的認知障礙，增強學生的空間想象能力.所以中學教師在面對學生較難理解的三維空間的立體圖形時，最佳的教學策略便是教師要多提供一些具體的實物模型，并讓學生自己也動手做一做，尤其是遇到翻折類的題型時，一定要讓學生多動手操作以增強直觀形象，提升直覺能力.

案例2棱柱歐氏定義的反例

筆者在聽中學教師講授棱柱定義這節課時，一般都會讓學生判斷這樣一個命題：“有兩個面平行，其余各面都是平行四邊形的多面體是棱柱”.而學生往往會認為是對的，此時教師就會給出一個如圖1的反例，以此來說明該命題的錯誤，從而佐證教材上的棱柱定義是正確的.顯然這個反例學生是較難想到的，因而需要教師告之.但事實上這個反例是有缺陷的，因為一般情況下的多面體都是指凸多面體，而該反例卻是凹的，因此數學程度好的學生會質疑，從而就很難判斷上述命題的真假.

其實，有數學史知識的教師應該知道，這個命題就是2 000多年前的古希臘數學家歐幾里得（Euclid，前330～前275）在《幾何原本》中下的棱柱定義，簡稱歐氏定義.當然現在知道這個定義是不對的，但就是這個錯誤的定義卻得到了歷史上許多數學家的認可，并整整統治了2 000多年，其原因就是長時間找不到歐氏定義的反例.也許中學教師會認為圖1的反例并不是很難，數學家怎么會想不到呢？所以問題就在于這個反例是凹的，可能當時歐幾里得就已經知道這個例子了，但他并不認可，因此只有找到一個凸的反例才具有說服力.在人類歷史上正是在找這個凸的反例時，讓數學家們整整花了2 000多年，直到20世紀初才找到，該反例便是圖2[14].很明顯，這個凸的反例學生根本想不到，這就需要教師自己動手做這個反例的實物模型，用事實說話來提升學生的直覺能力.

用實物模型來展現，可以讓學生感到既直觀明了又生動具體，從而使一些結論深刻地印在學生的腦海里.如案例2，學生看到這個凸的反例實物時一定會留下深刻印象的.事實上，數學中除了立體幾何外，還有一些比較抽象的概念也可借助實物模型來理解，如向量的概念，可用學生手中的“筆”來替代：筆尖表示向量方向，筆身表示向量的模，筆的移動表示向量的平移，這樣學生就會很快理解與“數”不同的“向量”；再如任意角的概念，可用學生身上的“手表”或教室里的“鐘”等實物來展現，就會讓學生很快突破以前所學的角范圍所帶來的束縛.

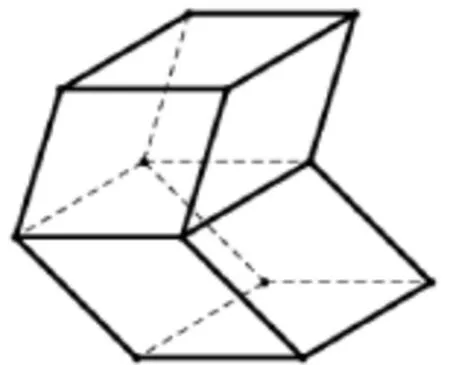
圖1

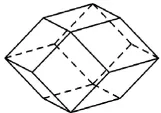
圖2

3.3 策略三：尋找數學原型，加深直覺認識

“隨著數學學習的深入，學生積累的數學知識和方法就成為了學生的‘數學現實’.這些現實應當成為學生進一步學習的素材，選用這些素材，不僅有利于學生理解所學知識的內涵，還能夠更好地揭示相關數學知識之間的內在關聯，有利于學生從整體上理解數學，構建數學認知結構”[15].根據對“數學現實”的詮釋，筆者認為可從學生已有生活常識出發，尋找數學知識原型，以加深直覺認識.

數學原型，其實就是指產生數學概念、法則、定理等知識的生活來源，或已得到論證的數學知識來作為直覺認識的一種模型.它包括日常生活中的原型和所學的數學知識作為模型.實際上，學生在前面的數學學習中也一直在利用數學原型，比如通過“向東向西”、“零上零下溫度”（數學原型）來形成“相反意義的量”，繼而來進一步理解“正負數”和“正負數加減法則”[15]；因式分解可由小學里學過的數的質因數分解作為數學原型來理解等等.

案例3“糖水不等式”的教學

在必修5《不等關系與不等式》的教學中，新課程標準教學要求“通過具體情境，感受在現實世界和日常生活中存在著大量的不等關系，了解不等式的現實背景.”比舊的教學大綱更側重于通過具體的情境讓學生感受新知，增加了對分析處理具體問題的要求.為了使學生在教師的引導下能通過直覺發現“糖水不等式”，并對該不等式的正確性有充分的認識，教師可以設計出如下的問題鏈：

問題1：同學們都知道，給糖水加糖能使糖水變甜.你們能把這一生活常識用數學式表達出來呢？（大部分學生可能會面露難色，不知從什么地方下手，原因是這里既沒有數字又沒有字母.面對此情景，教師繼續引導.）

問題2：解應用題列方程式時，未知數肯定沒有具體數據，那時你們是怎么辦的？（問題2使學生聯想到用字母表示數：設原來的糖水濃度為t1，加糖后的濃度為t2，則有

針對學生的思考，教師首先肯定他們抓住了問題的本質，即建立起一個不等式.教師緊接著拋出問題3.）

問題3：不足的是，式（1）沒有直接反映出“濃度”與“加糖”.你們能不能更具體地表示出“原濃度”、“加糖后的濃度”以及兩個濃度間的關系，使人一看這個“沒有任何漢字”的“符號”不等式，就能領會“糖水加糖更甜了”？（問題3會促使學生想到：設b克糖水里有a克糖，則，加糖后的糖水更甜了，就存在c＞0，使

當看到學生給出（2）式時，教師提出問題4.）

問題4：這里的c表示什么？是表示糖的質量嗎？濃度與質量能夠相加嗎！（問題4促使學生對（2）式中量的統一性產生思考，當學生們若有所思時，教師進一步追問.）

問題5：（2）式只表示了濃度增加則糖水就更甜，還沒有把濃度增加的原因——添糖反映出來.換句話說，當時，t2如何表示？（在問題5的刺激下，學生們會恍然大悟：，其中m＞0為所添糖的質量.由此得不等式：對b＞a＞0，m＞0，有.）

在原本比較枯燥的不等式教學中，教師從學生的已有生活常識出發，借助生活中的“給糖水加糖能使糖水變甜”這一數學原型引入，這樣不僅讓學生感受到生活中不等關系的存在，也知道生活中數學無處不在，激發起學生學習興趣的同時，加深了學生對“糖水不等式”的直覺認識，通過教師系列問題的“啟”和“發”使學生達到“憤”和“徘”的狀態，把學生的直覺思維一步一步地引向深入，引導學生達成對新知的高效認知.

又如，高中數學中的一些概念、性質和公式等也可通過尋找數學原型來幫助理解.比如：三角函數的單位圓定義，就以游樂場中的摩天輪作為數學原型：你坐在那里的位置就相當于單位圓上的一個點，然后當摩天輪轉動后，如何來表示你的位置？以這樣的生活現實來幫助學生認識三角函數的本質：刻畫具有周期性現象的圓周運動的函數模型.學生有了摩天輪作為單位圓的一個數學原型后，自然就會直觀認識到，的值不能超過1，同時有了這樣的數學直覺，也就不會犯算出sinα=2還作為答案的錯誤情況.再比如一些抽象函數，當具有性質時，則前者可用指數函數作為模型，后者可用對數函數f(x)f(y)=f(x+y)，f(xy)=f(x)+f(y)作為模型.這樣讓學生用已熟悉的具體函數作為數學原型就好理解，也容易解題了.

3.4 策略四：借助聯想思維，拓展直覺深度

聯想思維是產生直覺的先導.聯想是學生在認識數學對象的過程中，根據數學對象之間的某種聯系，由一個數學對象想到另一個相關數學對象的心理活動過程.數學問題解決的思維過程實質上是已知和未知間的一系列的聯想過程.當學生面對某些待解決且難以突破的新穎問題時，教師可引導學生通過仔細的觀察，必要時畫出示意圖，并聯想到一些思考方法接近的、形式相同的、結構特征相似的熟悉問題或常規問題，通過遷移將會頓悟出解決問題的思路和方法.

案例4祖暅原理的教學

為了使學生在教師的啟發下能通過直覺發現祖暅原理，并對該原理的正確性有充分的認識，教師可以先提出平面上的如下問題：

①不規則的圖形我們可以采用哪些方法求出它的面積的近似值？

②夾在兩條平行線間的兩個平面圖形被平行于這兩條直線的任意直線所截，如果截得的長度總相等，那么它們的面積有什么關系？你能說明理由嗎？

通過聯想，學生發現用平行分割、以直代曲的方法可把兩平面圖形的面積分成等積的平行四邊形或梯形的面積之和.易見二者面積的近似值是相等的.當分割數無限增大時，便可得出二者的面積相等的結論.教師緊接著又提出第三個問題：

③由以上的結論，請你猜想在空間會有什么類似的結論？你能說明其中大概的理由嗎？

以上過程中，教師由于引導學生進行漸進式的類比聯想，使學生不斷產生新的直覺最終“發現”祖暅原理，從而產生了認識上的飛躍.盡管其中的推理不甚嚴格，但卻使學生感受到了無限細分求和的極限思想.事實上，數學上的任何重大突破都萌發于這類樸素的直覺或靈感.

當然，數學中的聯想是多層次多角度的，除類比聯想、形似聯想外，還有對比聯想、接近聯想、關系聯想等等.但無論何種聯想都要以合理的數學認知結構為基礎，以合情的思維導向為原則.正確的聯想所引發的直覺往往可以在解題中收到“柳暗花明，曲徑通幽”的效果.

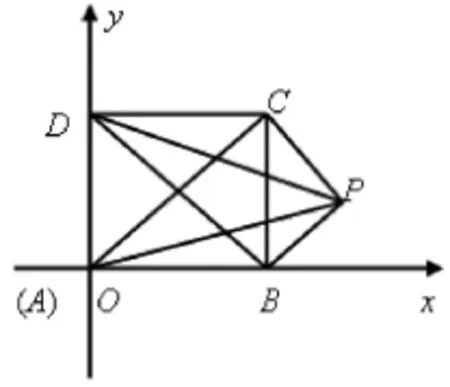
圖3

4 培養數學直覺需注意的問題與原則

我們在采用上述策略培養學生數學直覺能力的時候，需注意防止以下問題：其一，目的性不明.培養數學直覺是為了增強學生對所學知識的直觀認識，也是讓學生更好地理解數學知識，認清數學本質.如果僅僅是為了體現直觀性，而忽視數學知識的內在聯系和邏輯性，尤其是脫離數學的本質，那這樣就只停留在直覺的表象，對學生無任何幫助.其二，缺乏科學性，盲目培養.不管是數學實驗還是數學現實中的原型，都是對數學知識的直觀詮釋，即都能正確地刻畫數學知識.如果教師提供的模型并不能讓學生很好地理解數學知識，甚至是錯誤的，不僅不能培養數學直覺，而且還會誤導學生.

為了避免在培養數學直覺時出現上述兩個問題，需遵循一些原則：其一，適用性原則.不管設計的是數學實驗，還是提供實物模型和數學原型等，都要根據教學內容和學生已有的數學認知程度來考慮，只有正確反映數學知識的直觀教學才適用于學生，也有利于學生理解數學.其二，直觀性原則.教師讓學生完成某個數學實驗，再現某數學知識或展示某個模型，都要讓學生感到直觀形象，從而使學生能完成從感性認識到理性認識的順利過渡，提高學生的抽象思維能力，同時也加深直覺印象.其三，探究性原則.學生做完數學實驗后或在教師提供模型后，還要讓學生繼續探究，或觀察發現或歸納總結等，如案例1.而案例2，當學生看到實物模型后，還可深入探究怎樣得到這個反例，如可通過“補形”或“切割”等方法，這就需要推理和數學思維.如果抽象的推理以具體實驗或模型為依托，學生在研究實驗與模型的過程中就可獲得解決問題的啟發與靈感.

5 結束語

要讓學生在內心真正理解數學知識和接納新知，就必須要先對該知識有一個直覺感知，然后再在大腦中形成一個整體認識，繼而上升到抽象層面.筆者在對中學教師的聽課中歸納出來的這四種策略，對學生的數學直覺培養有一定的幫助.發現一個問題往往比解決問題更重要，而“發現”靠的并不都是邏輯思維，直觀性的思維和直覺能力有時更能出奇制勝.而在課堂上培養學生的數學直覺，既可使許多抽象和沉悶的概念、公式、定理、結論來得更易理解，也可避免本文開頭提到的中學教師所抱怨的這種現象.最后借用荷蘭哲學家斯賓諾莎的一句話作為本文的結束語：“只有通過直覺才可能直接認識一件事物的正確本質而不致陷于錯誤.”

[1]鄭君文，張恩華.數學學習論[M].南寧：廣西教育出版社，2003.

[2]周治金，趙曉川.直覺研究述評[J].心理科學進展，2005，13（6）：745-751.

[3]陸書環，傅海倫.數學教學論[M].北京：科學出版社，2004.

[4]俞國良.創造力心理學[M].杭州：浙江人民出版社，1996.

[5]汪安圣，朱祖祥.思維心理學習[M].上海：華東師范大學出版社，1992.

[6]喻平.數學教育心理學[M].南寧：廣西教育出版社，2004.

[7]格勞斯.數學教與學研究手冊[M].上海：上海教育出版社，1999.

[8]邵志芳.思維心理學（第二版）[M].上海：華東師范大學出版社，2007.

[9]朱德全.試論教學場情境的生成策略[J].高等教育研究，2004，25（6）：71-75.

[10]朱水根，王延文.中學數學教學導論[M].北京：教育科學出版社，2001.

[11]張大均.教育心理學（第二版）[M].北京：人民教育出版社，2004.

[12]葉彩虹.淺談中學數學直觀思維能力的培養[J].數學學習與研究，2010（20）：114-115.

[13]中華人民共和國教育部.普通高中數學課程標準[M].北京：人民教育出版社，2006.

[14]沈金興.一個需要完善的經典反例[J].中學數學，2015（3）：24-25.

[15]張奠宙，林永偉.關于“現實數學”和“數學現實”[J].數學教育學報，2008（2）：1-4.

Strategies for the Cultivation of Mathematic Intuitive Thinking

ZHANG Lei
（College of Mathematics&Statistics,Hanshan Normal University,Chaozhou,Guangdong,521041）

Mathematic intuition thinking is a cognitive ability,which can help one make a judgement quickly on the basis of certain knowledge and experience,by a overall observation of the object(and its constitution and relationships)of mathematics.Once a student gets mathematic intuition for certain knowledge,he/she can have deeper understanding of it,which will promote his/her imagery thinking as well as abstract thinking,so as to recognize the nature of mathematics.In specific mathematics teaching,we can follow four strategies to cultivate middle school students’ability of intuitive thinking:enhance students’perceptual intuition by create mathematic experiment;promote their intuitive abilities by physical model demonstrating;deepen their intuition cognition by finding mathematic prototype;expand depth of their intuition by the help of associative thinking, etc.

middle school students;mathematic intuition;cultivation;strategies

G 427

：A

：1007-6883（2016）06-0083-07

責任編輯 朱本華

2016-10-09

韓山師范學院2015年度教學改革項目（項目編號：HJG1524）.

張磊（1981-），男，河南確山人，韓山師范學院數學與統計學院講師.