一個不等式的證明及其推廣

吳 杉，余盛利，汪金漢

（1．湖北師范大學計算機科學學院，湖北黃石435002；2．湖北師范大學數學與統計學院，湖北黃石435002）

一個不等式的證明及其推廣

吳 杉1，余盛利2，汪金漢2

（1．湖北師范大學計算機科學學院，湖北黃石435002；2．湖北師范大學數學與統計學院，湖北黃石435002）

對于高等數學教材數學分析中的一個不等式，用兩種初等數學的方法給出了證明．將此不等式的右邊變形后，又得到兩個不等式，而且與普通高中課程《不等式選講》［4］中的不等式建立聯系，并對這些不等式做了六個推廣．

對稱性；排序不等式；推廣

在高等數學教材數學分析［1］中，對于一個初等的冪不等式，是根據凸函數的性質，利用詹森（Jansen）不等式給出的證明．本文首先用兩種簡單的初等數學方法給出了該不等式證明；其次將此不等式的右邊變形后，又得到兩個不等式，其中把一個不等式與普通高中課程標準實驗教科書．數學．不等式選講［2］中的不等式建立聯系；由于例1、例2、例3中三個不等式左邊都相同，在判斷它們右邊冪的乘積式大小時，例4中的（3）（ii）借助于Mathematic5．0軟件編程數據測試，而得到了一組數據．最后對這些不等式做了六個推廣．

在數學分析［1］中給出了一個證明冪不等式的例題：

例1 設a，b，c∈?＋，求證aabbcc≥（abc）

證法1（用詹森Jansen不等式） 設f（x）＝xlnx，x＞0．由f〃（x）＝＞0，（x＞0），知f（x）＝xlnx在x＞0時為嚴格凸函數，依詹森不等式有

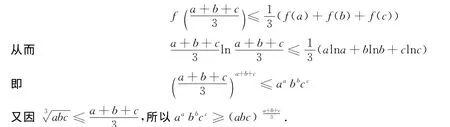
注：這里是高等數學中構造凸函數，利用函數的凸性，借助于詹森（Jansen）不等式和平均不等式得到證明．

下面給出兩種初等數學的證明方法。

證法2（商值比較法） 由于不等式是關于a，b，c對稱的，不妨設a≥b≥c＞0，則

注 該證法雖然非常簡單，但變形的技巧很強．

證法3（用排序不等式） 由對稱性，設a≥b≥c＞0，則lna≥lnb≥lnc，根據排序不等式，得

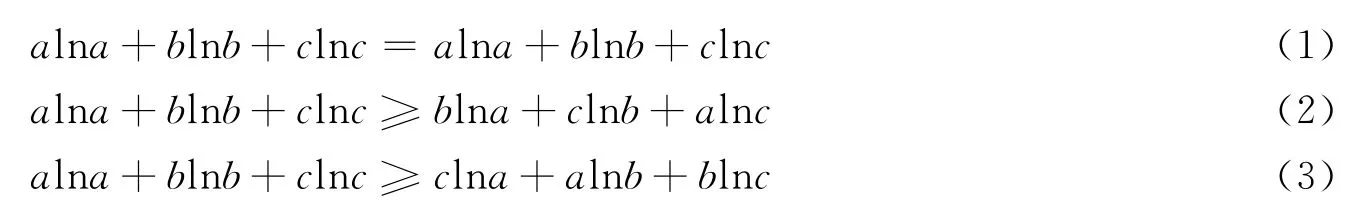
（1）＋（2）＋（3）得

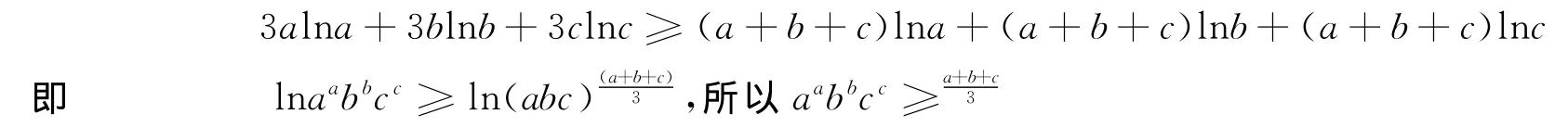
注 該證法關鍵是只有構造了兩個有順序的數組，才能利用排序不等式證明．

推廣1：設ai∈?＋（i＝1，2，…，n），求證

證明 序列｛ai｝與序列｛lnai｝有相同的大小順序，根據（初等數學）切比雪夫不等式，

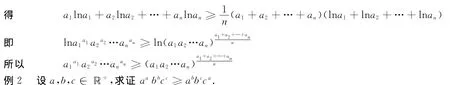
證明（用排序不等式）序列a，b，c，與序列lna，lnb，lnc，有相同的大小順序，根據排序不等式，

得 alna＋blnb＋clnc≥blna＋clnb＋alnc

于是，有 lnaabbcc≥lnabbcca

即aabbcc≥abbcca

推廣2 設ai∈＋（i＝1，2，…，n），an＋1＝a1，求證

推廣3 設ai∈＋＋（i＝1，2，…，n），求證其中ji（i＝1，2，…，n）是1，2，3，…，n的任一排列．

上述推廣2的不等式是推廣3不等式的特殊情形．推廣3的不等式的證明方法同例2．

證法1 原不等式等價于a2ab2bc2c≥ab＋cbc＋aca＋b，此不等式是新課標高中《不等式》［2］選講中的習題．只需證

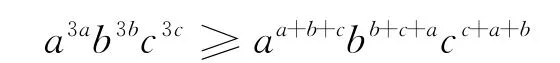
即等價于aabbcc≥（abc，而該不等式在例1中已證．故原不等式成立．

證法2 （商值比較法）由對稱性，不妨設則a≥b≥c＞0，則

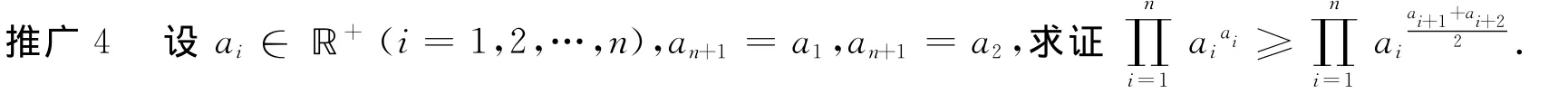
推廣5 設ai∈?＋（i＝1，2，…，n），求證，其中ki，mi（i＝1，2，…，n）分別是1，2，3，…，n的任一排列．

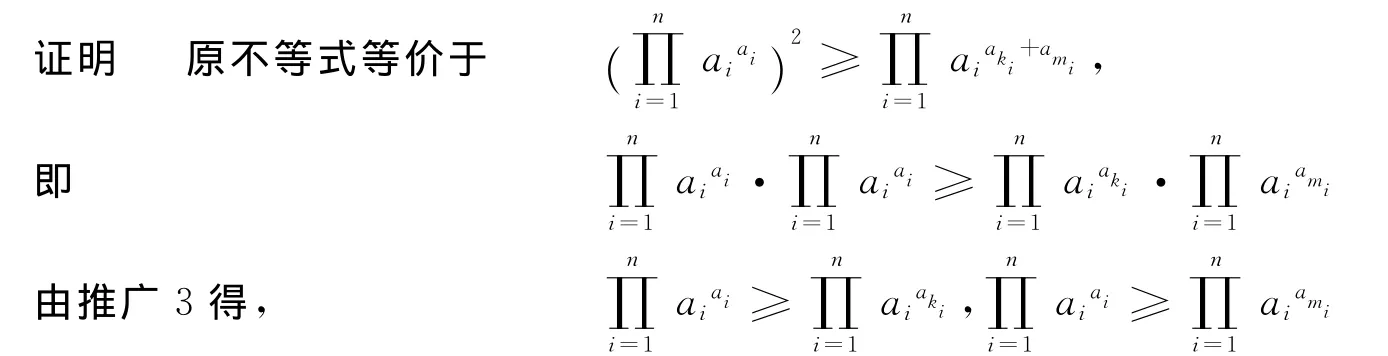
兩不等式相乘，即證推廣5．

上述推廣4的不等式是推廣5不等式的特殊情形．

由于例1、例2、例3中的三個不等式左邊都相同，下面比較這三個不等式右邊的冪的大小．例4 設a，b，c∈?＋，記x＝（abc，y＝abbcca，z＝abc，則（1）x≥z；（2）不能確定y與z的大小；（3）不能確定x與y的大小。證明 1）x≥z

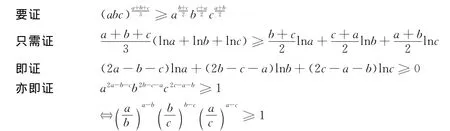
由對稱性，不妨設則a≥b≥c＞0，則a－b≥0，b－c≥0，a－c≥0≥1，≥1，≥1．

故上不等式成立，即證．x≥z．

2）i）取a＝1，b＝2，c＝3時，y＞z；

iii）顯然，可以使y＝z．

3）i）取a＝1，b＝1，0＜c＜1時，x＞y；

因此x＜y．

iii）顯然，可以使x＝y．

由1）推廣可得不等式：

推廣6：設ai∈?＋（i＝1，2，…，n，n≥3），求證

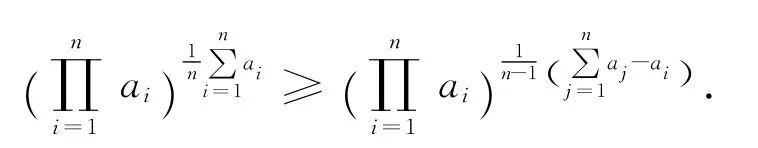
由不等式的對稱性，不妨設a1≥a2≥…≥an，根據排序不等式，有

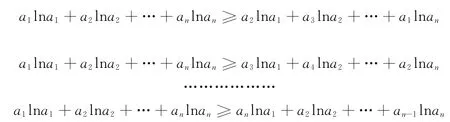
把上面n－1個不等式相加即證原不等式．

此不等式即為推廣1．證畢．

［1］華東師范大學數學系．數學分析（上冊）（第三版）．［M］．北京：高等教育出版社，2001．

［2］人民教育出版社，課程教材研究所，中學數學課程教材研究開發中心．普通高中課程標準實驗教科書，數學，不等式選講［M］．北京：人民教育出版社，2007．

［3］余元希，田萬海，毛宏德．初等代數研究下冊［M］．北京：高等教育出版社，1988．

［4］余盛利，程 艦，文遠航．詹森（Jensen）不等式在求幾何最值與證明幾何不等式中的應用［J］．湖北師范學院學報（自然科學版），2015，35（1）：105～109．

G250

A

009－2714（2016）04－0110－04

10．3969／j．issn．1009－2714．2016．04．024

2016—03—14

吳杉（1986— ），男，湖北荊門人，講師，碩士，研究方向為微分方程與控制論．