如何提高學生的數學應用題解答能力

□周麗娜

如何提高學生的數學應用題解答能力

□周麗娜

文章結合高中數學教學案例，從數學讀題能力的培養、數學建模能力的培養、數學解題能力的培養3個方面探討了提高學生解答數學應用題能力的問題。

高中數學；數學應用題；解題能力

《普通高中數學課程標準 (實驗)》把“發展學生的數學應用意識”作為課程基本理念之一，要貫徹落實這一理念就必須重視數學應用題的教學。通常把來源于客觀世界具有實際意義或實際背景的、能轉化為數學形式表示、可運用數學知識獲得解決的一類問題稱為數學應用題。解答數學應用題，需具備一定的數學綜合能力，包括數學讀題能力、數學建模能力、數學解題能力等。應用題在高考試卷中占據重要地位，但學生的得分率卻較低。為此筆者結合教學實踐，就提高學生解答數學應用題的能力進行了初步的探索。

一、數學讀題能力的培養

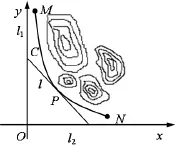
圖1

“數學教學就是數學語言的教學。”數學閱讀既是一個心理認知過程，也是一個不斷假設、證明、想象、推理的數學思維過程。數學讀題能力的培養需要將文字、數學符號語和圖形等語言有機互譯，靈活轉化。

【案例1】（2015年高考江蘇卷第17題）某山區外圍有兩條互相垂直的直線型公路，為進一步改善山區的交通現狀，計劃修建一條連接兩條公路的山區邊界的直線型公路，設兩條互相垂直的公路為l1、l2，山區邊界曲線為C，計劃修建的公路為l，見圖1，M、N為C的兩個端點，測得點M到l1、l2的距離分別為5千米和40千米，點N到l1、l2的距離分別為20千米和2.5千米，以l1、l2所在的直線分別為x、y軸，建立平面直角坐標系xoy，假設曲線C符合函數（其中a、b為常數）模型。

（1）求a、b的值。

（2）設公路l與曲線C相切于P點，P的橫坐標為t。①請寫出公路長度的函數解析式，并寫出其定義域；②當t為何值時，公路l的長度最短？求出最短長度。

1.指導學生有效讀題的一般程序

第一遍快速瀏覽了解概況：本題是修路問題，跟長度有關，應馬上聯想到一些求距離的公式，讀懂圖1，注意曲線C的模型和字母M、N；第二遍收集有效信息，劃出關鍵詞句，數形結合進行理解分析：確定點M坐標（5，40），N坐標（20，2.5），函數模型已知，兩個方程兩個未知量足以；第三遍仔細閱讀，找出附加或限制條件作上記號，為后續解題做好充分準備。

2.教師的教學策略

（1）指導學生養成自主讀題的習慣。平時學生一般不重視數學讀題，教師也總喜歡把自己的理解灌輸給學生，這就使得學生普遍缺乏閱讀數學課本和資料的習慣，這種現狀迫切需要改變。蘇教版高中數學每冊教材的“探究拓展”欄目中都配有一定數量生動、新穎的應用題，教師可引導學生多讀、多練，從而逐步養成自主讀題的習慣。

（2）提高學生的讀題技能，加強讀題交流。按有效讀題程序加強訓練，在第一遍讀題后，可請不同層次的學生口頭表達自己的理解過程，再讓其他學生補充，教師及時給予評價和鼓勵。應用題的讀題一定要舍得花時間，只有學生的理解分析能力提高了，讀題速度和水平才會提高，成功解題的自信心也才會增強。

二、數學建模能力的培養

“數學建模是運用數學思想、方法和知識解決實際問題的過程。”培養學生的數學建模能力，不僅是貫徹落實新課程基本理念的需要，更是激發學生學習數學的興趣，改變學生數學學習方式，發展學生創新意識和實踐能力的需要。

【案例2】某公園有個池塘，其形狀為直角△ABC，∠C=90°，AB=200米，BC=100米。①現在準備養一批供游客觀賞的魚，在AB、BC、CA上分別取點D、E、F（見圖2），使得EF∥AB，EF⊥ED，在△DEF中喂魚，求△DEF面積的最大值；②現在準備新建一個河塘，在AB、BC、CA上分別取點D、E、F（見圖3），建造△DEF連廊（不考慮寬度）供游客休息，且使△DEF為正三角形，求△DEF邊長的最小值。

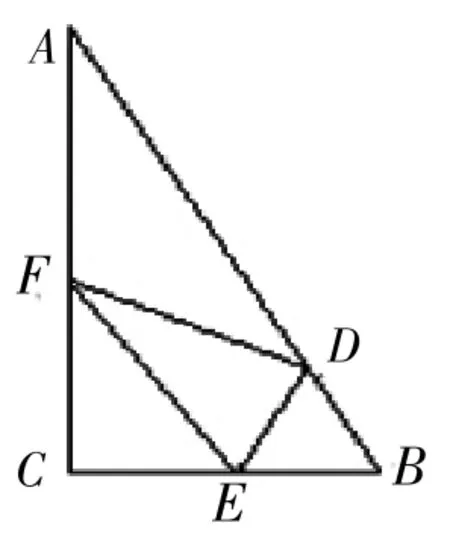
圖2

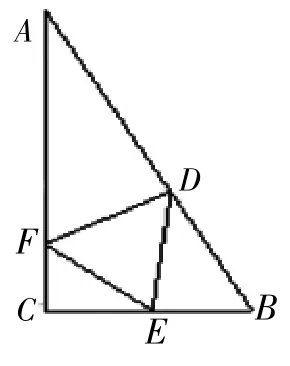
圖3

1.指導學生掌握建模的一般程序

（1）實際問題數學化。從問題出發，把三角形面積、邊長的最值問題轉化為函數的值域問題。

（2）針對函數值域問題，確定相應的自變量和應變量。問題①是一個直角三角形面積的最值問題，自變量自然要轉到兩條直角邊上。由于點E在直角△ABC的邊BC上滑動，根據題意發現△ABC、△CEF、△BDE為相似三角形，故可設CE或BE為x，用x表示兩條直角邊EF、DE；問題②可把正三角形邊長作為應變量，聯系三角知識，可轉化到正、余弦定理，故應變量自然要選擇角，設直角△CEF的其中一個銳角為自變量。通過逆向思維，可找到符合本題的數學知識。

（3）分析本題，將數學問題符號化。

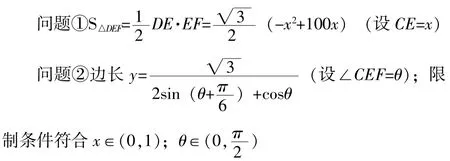
2.教師的教學策略

（1）聯系數學現實進行教學。平時多結合數學現實進行教學，問題情境設計多選擇生產生活的實例，蘇教版教材中也有很多可以引用的具體例子。此外，還可引導學生在日常生活中多用數學思想、方法和知識嘗試解決周圍的實際問題。

（2）針對學生現實因材施教。教師要轉變數學教學觀念和方法，重視數學知識的生活來源與應用價值的介紹、數學知識的建構過程與方法的教學，同時要認真分析學情，針對學生的數學實際水平，分層設計一些有新意的建模情境，激發學生探究的欲望。

（3）緊扣教材進行提升拓展。新教材很好地體現了數學來源于生活，又服務于生活的理念。近年來江蘇省高考數學卷中的應用題背景都能在教材中找到，如2014年的古橋保護問題、2013年三角形背景的下山行程問題、2012年炮彈發射問題等。所以教師應緊扣教材進行提升拓展，爭取實現學生能力發展與高考成績的雙豐收。

三、數學解題能力的培養

“高中數學課程應注意提高學生的數學思維能力，這是數學教育的基本目標之一。”筆者認為，培養學生的數學解題能力應是提高學生數學思維能力的核心。

【案例3】某企業投入81萬元經銷某種產品，經銷時間共60個月，市場調研表明，該企業在經銷這個產品期間第x個月的利潤符合f（單位：萬元），為獲得更多利潤，企業將每月獲得的利潤投入到次月的經營中，設第x個月的當月利潤率g（x）=如g（10）；②求第x個月的當月利潤率g（x）；③該企業經銷此產品期間，哪個月的當月利潤率最大，并求該月的當月利潤率。

1.指導學生掌握解題的一般程序

（1）審題很重要。

（2）由特殊到一般。

（4）寫成分段函數形式。

（5）函數最值問題的關鍵是單調性。根據g（x）第一段直接利用單調性可知g（1）最大，第二段利用基本不等式，最值求出不代表結束，注意限制條件，“當且僅當即x=40”。

（6）概念要清晰。分段函數并不是兩個函數，故每段最值必須比較大小，取其中較大那個

（7）書寫要完整。最后把“答”寫上。

2.教師的教學策略

（1）重視數學思想與方法。培養數學解題能力應引導學生對題目信息仔細分析，關注解題后對問題本質的挖掘和反思，重視基本概念反映的思想與方法，讓解題思路來得自然一些。

（2）不要過于重視結論。目前，學生存在重結論輕過程、重方法輕思想的弊病，因而要加強實踐演練，使學生體會解題的過程與方法，形成有效解題的策略。

總之，提高學生解答應用題的能力，需要教師提高學生對應用題學習的興趣，重視“數學化”思想的教學過程，并從數學讀題、數學建模、數學解題3個方面加強指導和訓練。

[1]教育部.普通高中數學課程標準(實驗)[S].北京:人民教育出版社,2003.

[2]沈翔.國際數學教育運動中應用問題概述[J].數學通訊,1999,(8).

（編輯：易繼斌）

G633.6

A

1671-0568（2016）33-0082-02

周麗娜，江蘇省昆山中學教師。