開縫空腔抑制翼型跨聲速抖振的數值模擬

周偉， 張正科,*， 屈科， 翟琪

1.西北工業大學 航空學院， 西安 710072 2.紐約城市大學 城市學院 土木工程系， 紐約 NY10031

開縫空腔抑制翼型跨聲速抖振的數值模擬

周偉1， 張正科1,*， 屈科2， 翟琪1

1.西北工業大學 航空學院， 西安 710072 2.紐約城市大學 城市學院 土木工程系， 紐約 NY10031

采用非定常雷諾平均 Navier-Stokes(URANS)方法計算了18%雙圓弧翼型的跨聲速抖振特性，分析了翼面激波振蕩及流場結構演化的特點，研究了在翼型表面開通氣空腔抑制跨聲速抖振的可行性，對空腔深度、開縫數目對激波振蕩的抑制效果進行了對比分析。計算發現，18%雙圓弧翼型的跨聲速激波自激振蕩只有向前的運動，沒有向后的運動，開縫空腔能夠抑制翼型跨聲速抖振，但對抖振頻率影響不大；空腔深度大，抑制效果好，但空腔深度變化對振蕩頻率影響不大；開2、3、4個槽縫抑制抖振的效果差別不大，開縫數量對抖振頻率影響不大。

跨聲速； 抖振； 激波振蕩； 空腔； 抑制

翼型跨聲速抖振是升力面上激波與部分分離或完全分離的邊界層相互作用產生的一種跨聲速不穩定流動現象，主要由激波/邊界層相互干擾引起，因此跨聲速抖振又稱激波抖振或激波誘導振蕩。跨聲速抖振出現在很多航空領域，如內流中的葉輪機械葉片繞流、外流中的飛行器繞流等。跨聲速抖振受控于一個主要頻率，典型的跨聲速抖振減縮頻率與運輸機和戰斗機典型的低頻彈性模態是一個量級。激波運動及其相關的流場振蕩影響氣動力和力矩的變化，氣動力和力矩反過來與彈性結構相互作用可能影響飛行器的結構完整性和操縱品質。因此，跨聲速抖振在跨聲速飛行器設計中成為一個需要著重考慮的因素。

為理解抖振的特性和物理機理，人們已經開展了很多相關研究工作。Tijdeman[1]通過對帶振蕩襟翼的NACA64A006翼型的實驗研究，總結了激波振蕩3種可能的形式。McDevitt等[2-3]對厚度為18%的雙圓弧翼型在零迎角跨聲速條件下進行了實驗研究，發現了激波振蕩現象，并研究了迎角、前后緣分離的影響，測量了激波振蕩頻率。Lee[4]對激波抖振的研究進行了綜述和回顧，其中還包括一些激波抖振機理的物理模型。Gillan[5]基于Baldwin-Lomax代數湍流模型數值預測了18%相對厚度的雙圓弧翼型上的激波誘導振蕩。Bartels[6]求解了薄層Navier-Stokes方程并引入k-ω湍流模型，進行了激波抖振起始的計算。Raghunathan等[7]利用薄層Navier-Stokes方程研究了后緣在激波振蕩機理中的重要作用。Deck[8]采用分區DES(Detached Eddy Simulation)方法研究了超臨界翼型的跨聲速抖振現象，并分析了激波運動和激波誘導分離的演化過程。

采取減小激波振蕩的振幅或推遲振蕩至更大馬赫數或更大迎角的措施能擴大機翼的抖振邊界。實驗和數值計算研究表明，跨聲速翼型上周期性激波運動與尾跡區域是相互耦合的。可通過改善激波/邊界層干擾區域內的流場或靠近后緣尾跡區內的流場來控制激波的振蕩。控制激波邊界層相互作用最常用的方法是吹氣或吸氣。控制后緣尾跡區流動的方法主要有：增加后緣厚度、在后緣處安裝偏轉器等。Thiede等[9]在VFW VA-2超臨界翼型上研究了3種吸氣結構，即單縫、雙縫和多孔板模型，發現在無機械吸氣裝置下雙縫和多孔板模型可以延遲激波誘導分離的發展，但要付出性能降低的代價。Gibb[10]提出在激波下游某處安裝金屬絲線以固定激波誘導分離位置，抑制了周期性激波運動，但尾跡明顯變大、阻力大幅增加。Caruana等[11]通過在后緣處安裝偏轉器的主動控制方法實現了對激波振蕩的抑制，延緩了抖振的發生，改善了抖振邊界。

本文采用常用軟件中的非定常雷諾平均Navier-Stokes(URANS)方法，計算模擬了18%厚度雙圓弧翼型的跨聲速抖振，分析了激波周期性運動的流場結構的演化、翼面及尾跡的壓力特性等，并探討了開縫空腔這一被動控制措施對翼型跨聲速抖振的抑制效果。

1 抖振計算與數值方法驗證

以18%厚度雙圓弧翼型為研究對象，采用URANS方法和剪切應力輸運(SST)湍流模型數值計算翼型跨聲速抖振，來流條件為：馬赫數Ma=0.76，迎角α=0°，基于弦長(c=1.0 m)的雷諾數Re=11×106，翼型網格數為633×145，第一層網格間距滿足y+=1。圖1為雙圓弧翼型的C型網格圖。圖2為上述計算條件下上翼面時均壓力系數Cp與實驗值[2]的比較，橫坐標x/c為相對弦向位置，可以看出，計算結果與實驗值吻合較好。

圖3為翼型升力系數CL、阻力系數CD和俯仰力矩系數Cm隨時間t的變化，它們呈正弦振蕩變化，顯示了翼型跨聲速抖振發生時流場的非定常性。

圖4為采用Welch方法對升力系數振蕩進行傅里葉變換得到的功率譜密度(Power Spectral Density, PSD)圖。由于抖振發生時脈動能量最大，因此圖4中功率譜密度峰值對應的頻率即為翼型跨聲速抖振頻率，其值為f=41.56 Hz，對應的減縮頻率k=πfc/U∞=0.49，U∞為來流速度，與文獻[3]中實驗所得k=0.495較為吻合。以上時均壓力分布、減縮頻率與相關實驗數據的接近與吻合說明所用數值方法模擬18%厚度雙圓弧翼型跨聲速抖振是可行的。

圖1 雙圓弧翼型C型局部網格

Fig.1 Local C-type grid of biconvex circular-arc airfoil

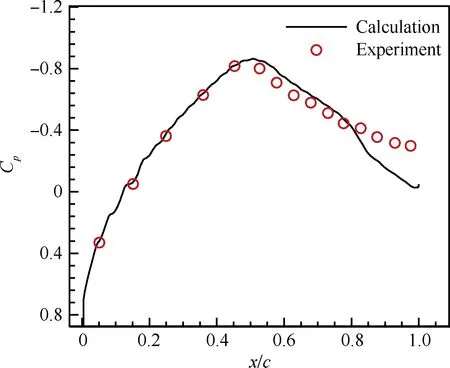
圖2 上翼面時均壓力系數分布

Fig.2 Time-averaged pressure coefficient distribution on upper airfoil surface

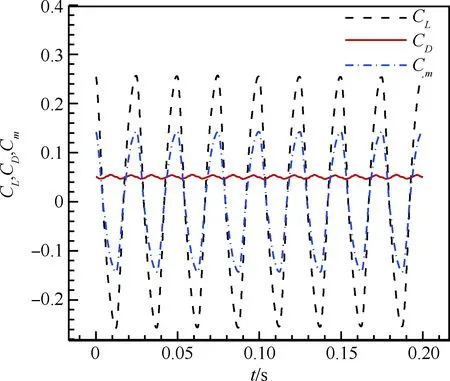
圖3 升力、阻力和俯仰力矩系數對時間的變化

Fig.3 Variation of lift, drag and pitching moment coefficients with time

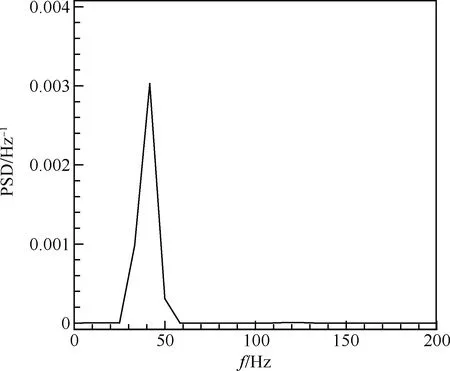
圖4 翼型升力系數功率譜密度(PSD)

Fig.4 Power spectral density (PSD) of airfoil lift coefficient

圖5給出了升力系數一個振蕩周期內6個不同時刻的馬赫數云圖(t*為無量綱時間)。從圖中可以清楚地看到翼面激波的周期性運動及激波/邊界層相互作用區域的變化。圖5(a)～圖5(e)顯示了上翼面激波的向前運動及強度減弱過程，直到它在圖5(e)所示的t*=0.76的位置時消失。在t*=0.76～1.00之間，上翼面激波可能繼續向前運動，并退化為弱壓力波，以向上游傳播的聲波的形式離開翼型[4]。在圖5(f)中(t*=1.00)，上翼面激波已回到它振蕩運動所能達到的最下游位置(假設它有向后運動)，或者說它突然又重新復活在它運動所能及的最下游位置(假設t*=0.76后它向前運動到上游流動)，即將開始下一輪的向前運動。下翼面的激波也在作類似的周期性運動，只是相位有偏差。隨著激波的運動，上下翼面波后的附面層也在交替地經歷著厚度變化。圖6為一個周期內上翼面壓力系數分布圖，可以看到激波只有前移運動，未出現向后運動。

圖5 一個周期內不同時刻的馬赫數云圖(Ma=0.76,α=0°,Re=11×106)

Fig.5 Mach number contours at different instants in one cycle (Ma=0.76,α=0°,Re=11×106)

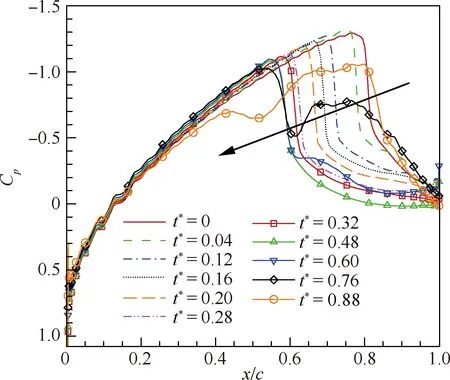
圖6 一個周期內不同時刻上翼面壓力系數分布

Fig.6 Pressure coefficient distribution on upper airfoil surface at different instants in one cycle

圖7為上翼面x/c=0.4，0.6，0.7，0.8，0.9這5個不同位置處壓力系數隨時間的變化，圖8為尾跡區x/c=1.25, 1.50, 2.00, 3.00這4個不同位置處壓力系數隨時間的變化。由圖7和圖8 可看出，翼面和尾跡區壓力隨時間的變化都呈現一定的振蕩性。在x/c≤0.8時，翼面壓力振蕩幅值隨弦向距離增大而增大，x/c=0.8時幅值達到最大，x/c=0.9時，幅值急劇減小。尾跡區壓力振蕩的不規則性變強，其振蕩幅值要比翼面小得多，越往下游，振幅越小，在大于3倍弦長遠的尾跡處壓力振蕩已經很小，其時均值已接近于零，說明此處壓力基本恢復至來流壓力。

圖9給出了x/c=0.7弦向點處上下翼面的壓力振蕩比較，可以看出上下翼面的激波振蕩是交替進行的，且通過傅里葉相位變換，得到它們運動的相位差為180°，說明上下翼面的激波運動是反相位的，驗證了圖5所觀察到的上下翼面激波運動是交替的直觀結論。圖10給出了翼型上不同點處壓力振蕩的功率譜密度圖，通過比較得知，各點的壓力振蕩頻率是一致的，在x/c=0.4處振蕩能量很小，接近于0，說明激波在前移過程中已逐步減弱(退化)為壓力波。

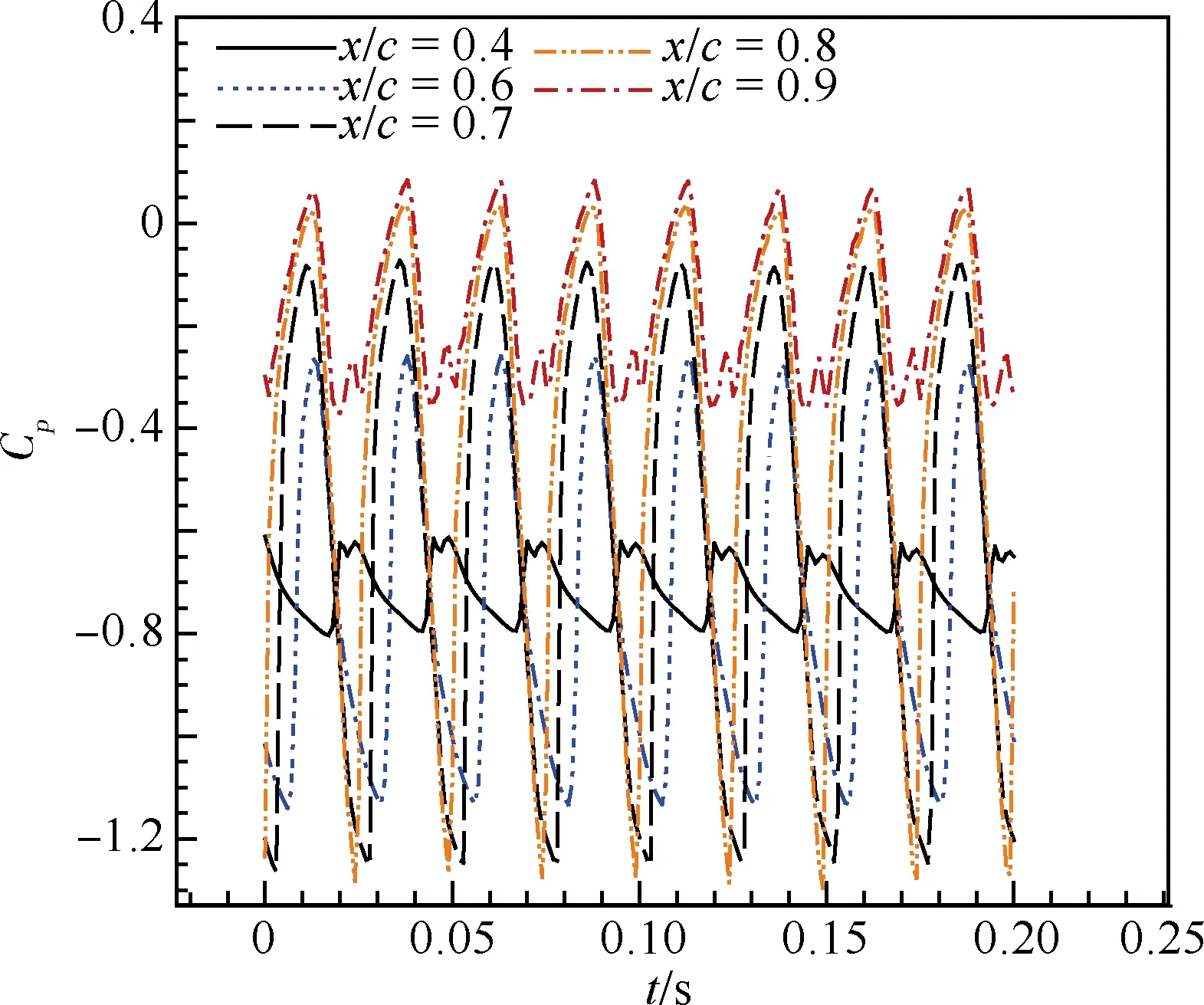
圖7 上翼面不同弦向位置處壓力振蕩

Fig.7 Pressure oscillations at different chordwise positions on upper airfoil surface

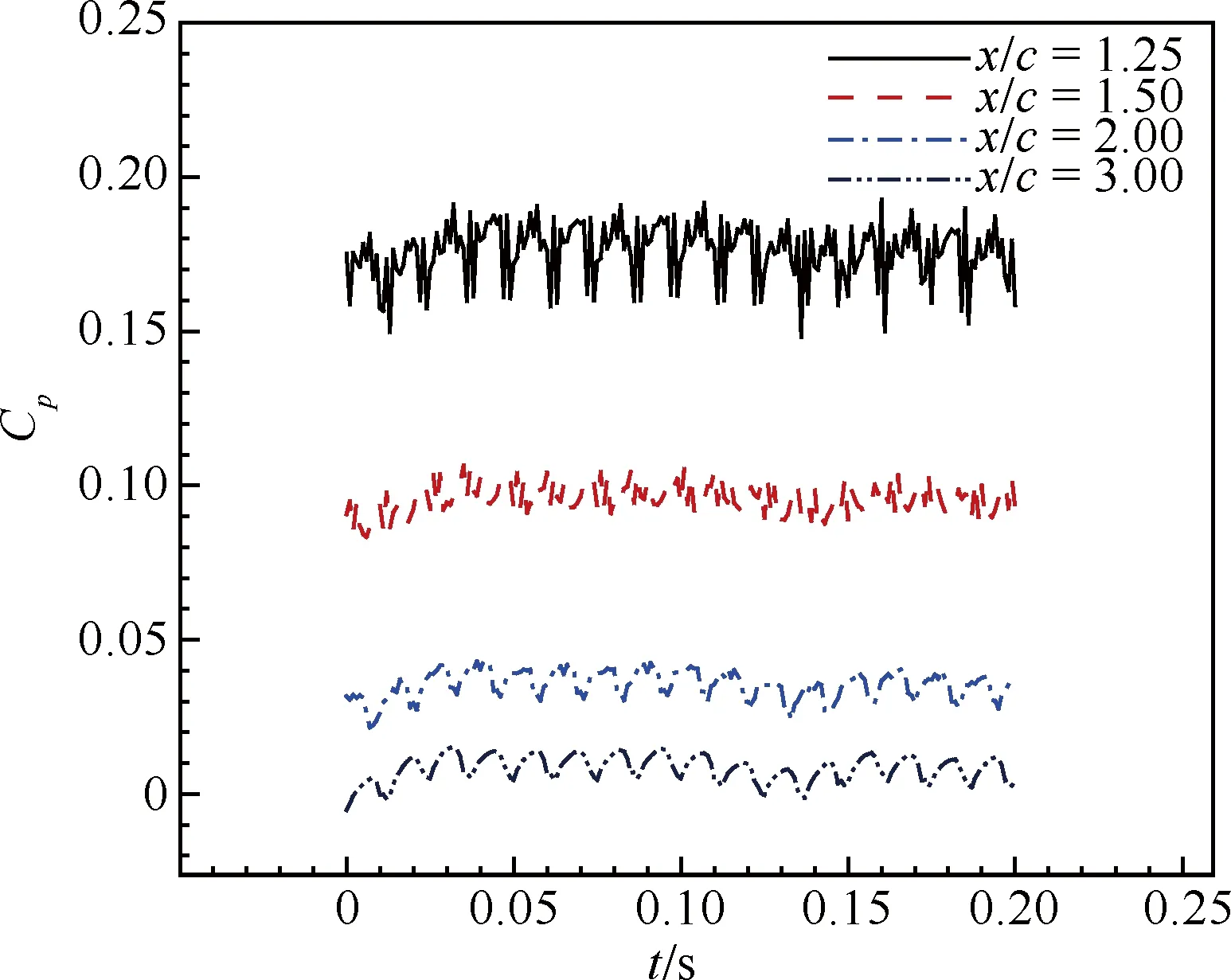
圖8 尾跡區不同位置處壓力振蕩

Fig.8 Pressure oscillations at different positions in wake region

圖9 上下翼面壓力振蕩(x/c=0.7)

Fig.9 Pressure oscillations on upper and lower airfoil surfaces (x/c=0.7)

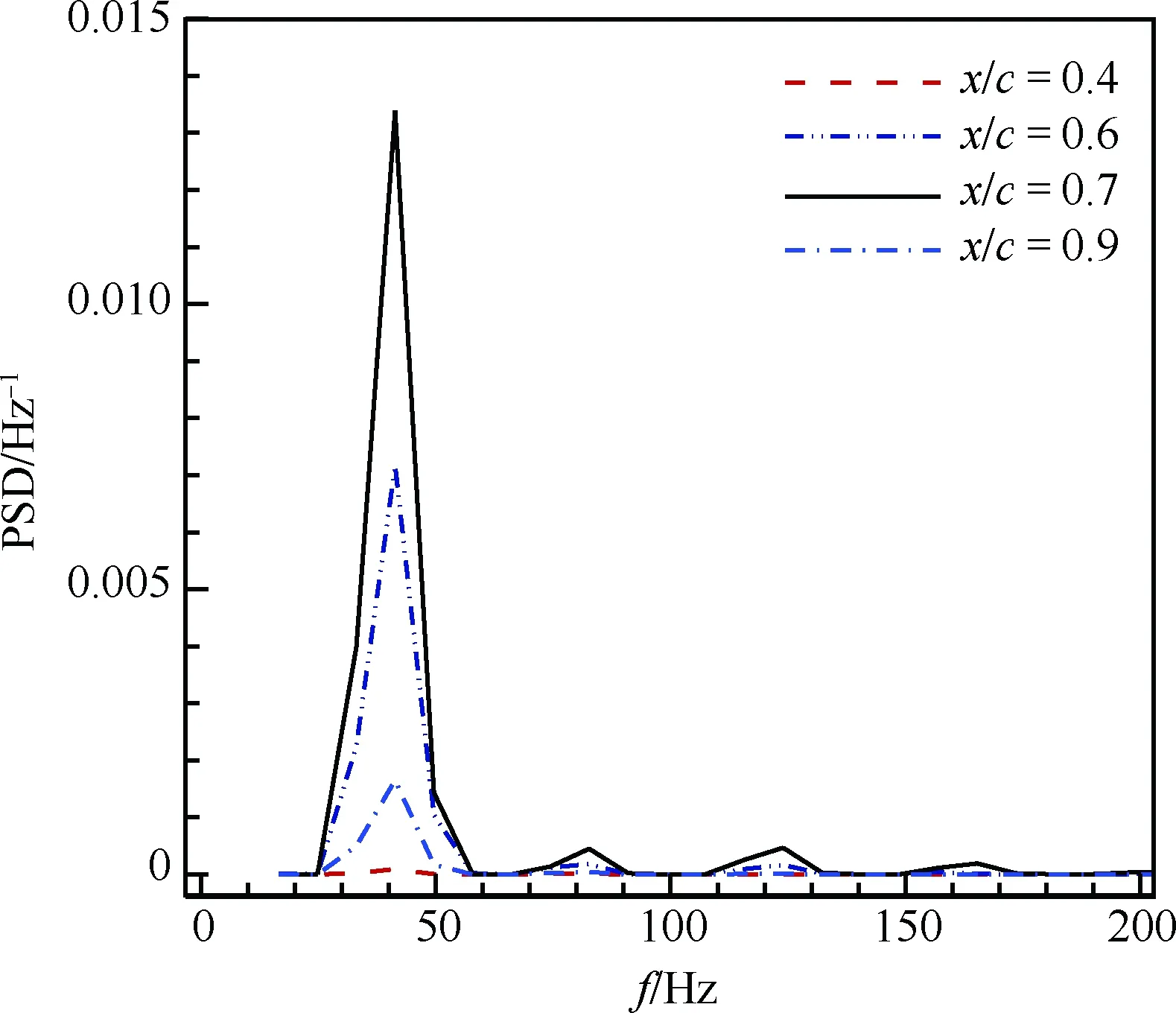
圖10 不同弦向位置處壓力振蕩功率譜密度

Fig.10 PSD of pressure oscillations at different chordwise positions

2 開縫空腔對激波振蕩抑制的數值分析

2.1 雙縫空腔對激波振蕩的抑制效果

Thiede等的研究[9]說明，翼面通氣雙縫或通氣板有緩解激波誘導分離的作用，而單縫就幾乎沒有效果。本節選擇在18%相對厚度的雙圓弧翼型上開2個通過翼面下的空腔相連通的槽縫，來檢驗這種構型對跨聲速激波抖振的抑制作用。兩個槽縫編號分別為A和B，寬度為10 mm，槽縫的中心線與翼面垂直，縫A中心位于x/c=0.70處，縫B中心位于x/c=0.75(x為從翼型前緣算起的弦向坐標)處，空腔前端位于x/c=0.663處，后端位于x/c=0.797處，腔長L=134 mm，空腔的底部位于弦線上，空腔及槽縫幾何結構如圖11所示。將此構型標記為“雙縫深腔”(2-slot Deep Cavity)。將沒有施加控制措施的翼型稱為基準翼型(Baseline Airfoil)。圖12為帶雙縫深腔的翼型網格。

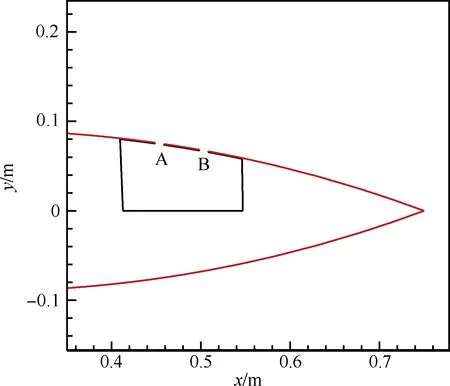
圖11 雙縫空腔翼型幾何構型

Fig.11 Configuration of airfoil with a cavity ventilated by two slots

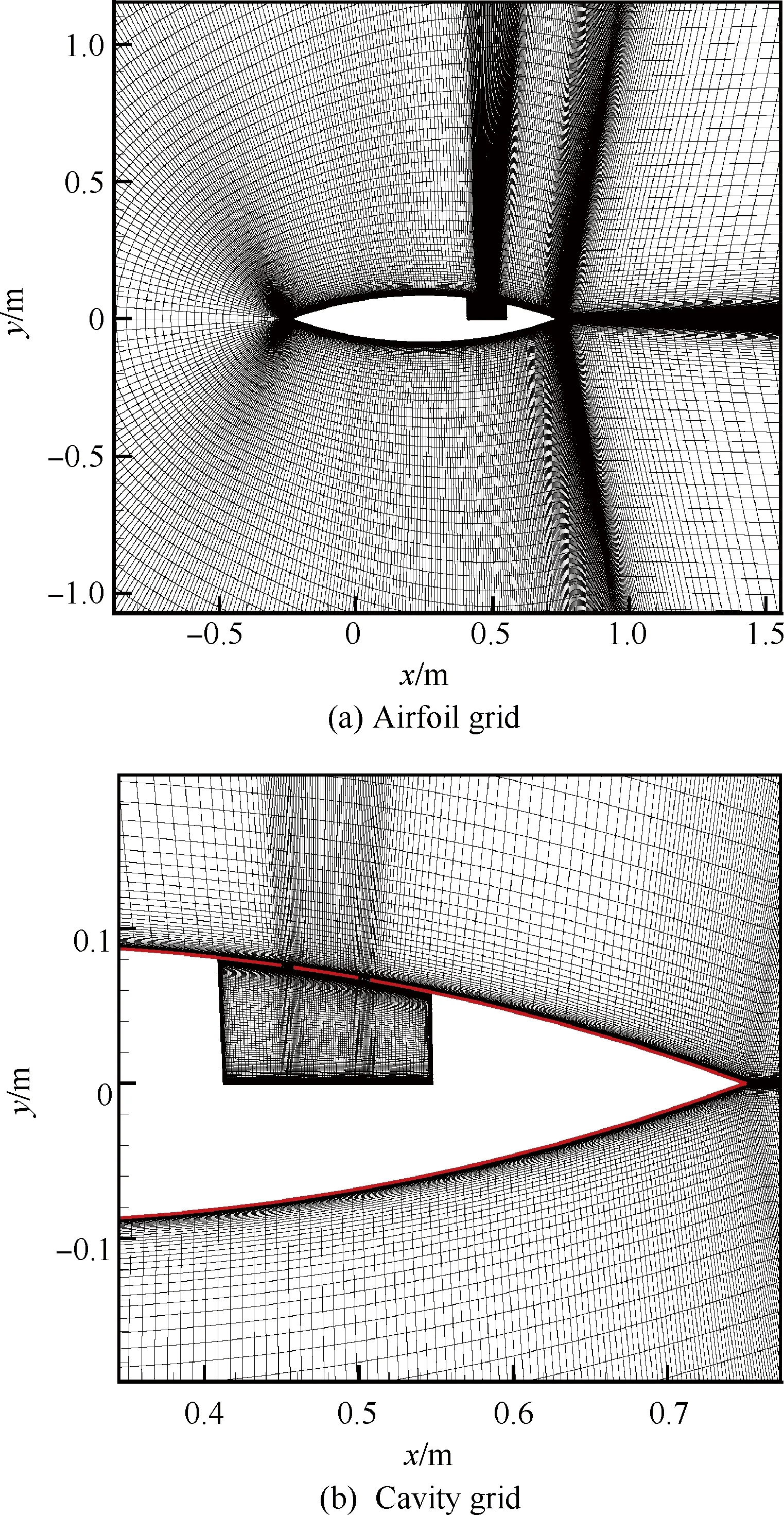
圖12 雙縫空腔翼型網格

Fig.12 Grid of airfoil with a cavity ventilated by two slots

計算條件與第1節基準翼型一致。圖13和圖14給出了計算的翼型升力系數、俯仰力矩系數隨時間變化歷程與基準翼型的比較。由圖可知，帶雙縫空腔翼型的升力系數和俯仰力矩系數振蕩幅值比基準翼型有明顯減小，表明翼型跨聲速抖振強度減弱了。圖15和圖16給出了升力系數和俯仰力矩系數功率譜密度圖的比較。可以看出，翼面開槽后的抖振頻率(f2-slot=40.56 Hz)與基準翼型的抖振頻率(fbaseline=41.66 Hz)很接近。除了抖振這個主頻率之外，還存在一個比抖振頻率稍高的頻率(f≈81 Hz)，這可能是由于翼面開縫開腔所造成的。

圖17給出了一個周期內6個不同時刻所對應的馬赫數云圖，與基準翼型一個周期內的不同時刻馬赫數云圖對比發現，上翼面由于開縫，造成激波強度在開縫處減弱，減弱了激波邊界層的相互干擾。

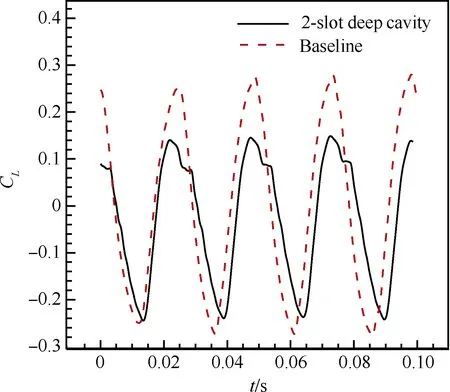
圖13 升力系數振蕩比較

Fig.13 Comparison of lift coefficients oscillations

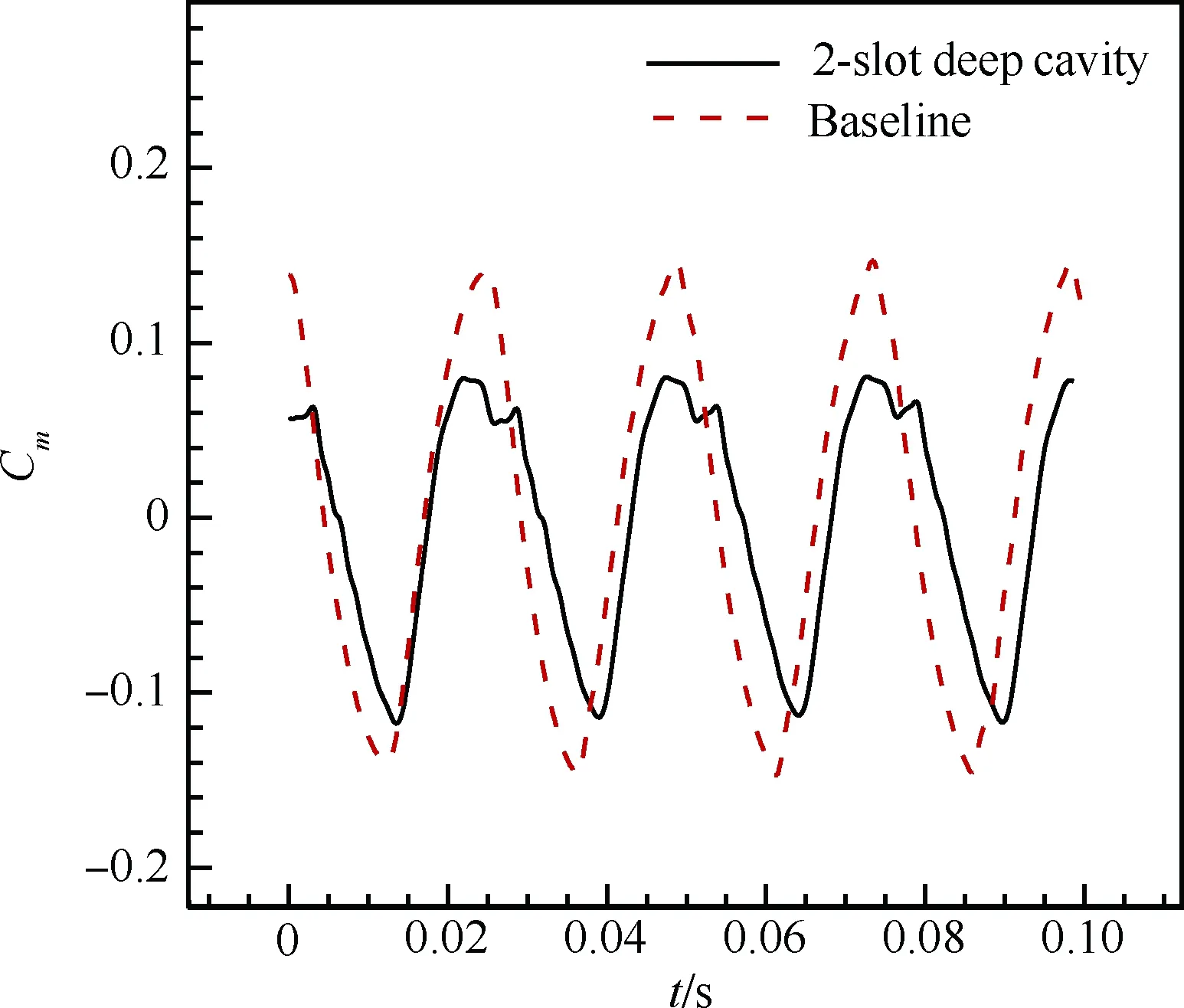
圖14 俯仰力矩系數振蕩比較

Fig.14 Comparison of pitching moment coefficients oscillations

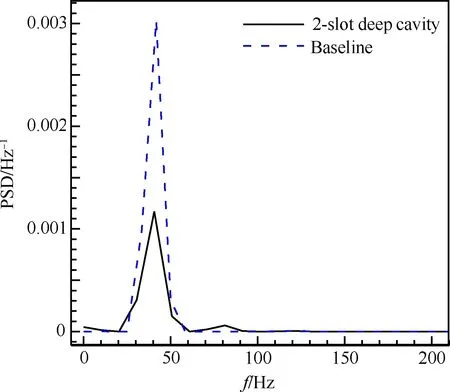
圖15 升力系數功率譜密度振蕩比較

Fig.15 Comparison of PSD of lift coefficients oscillations

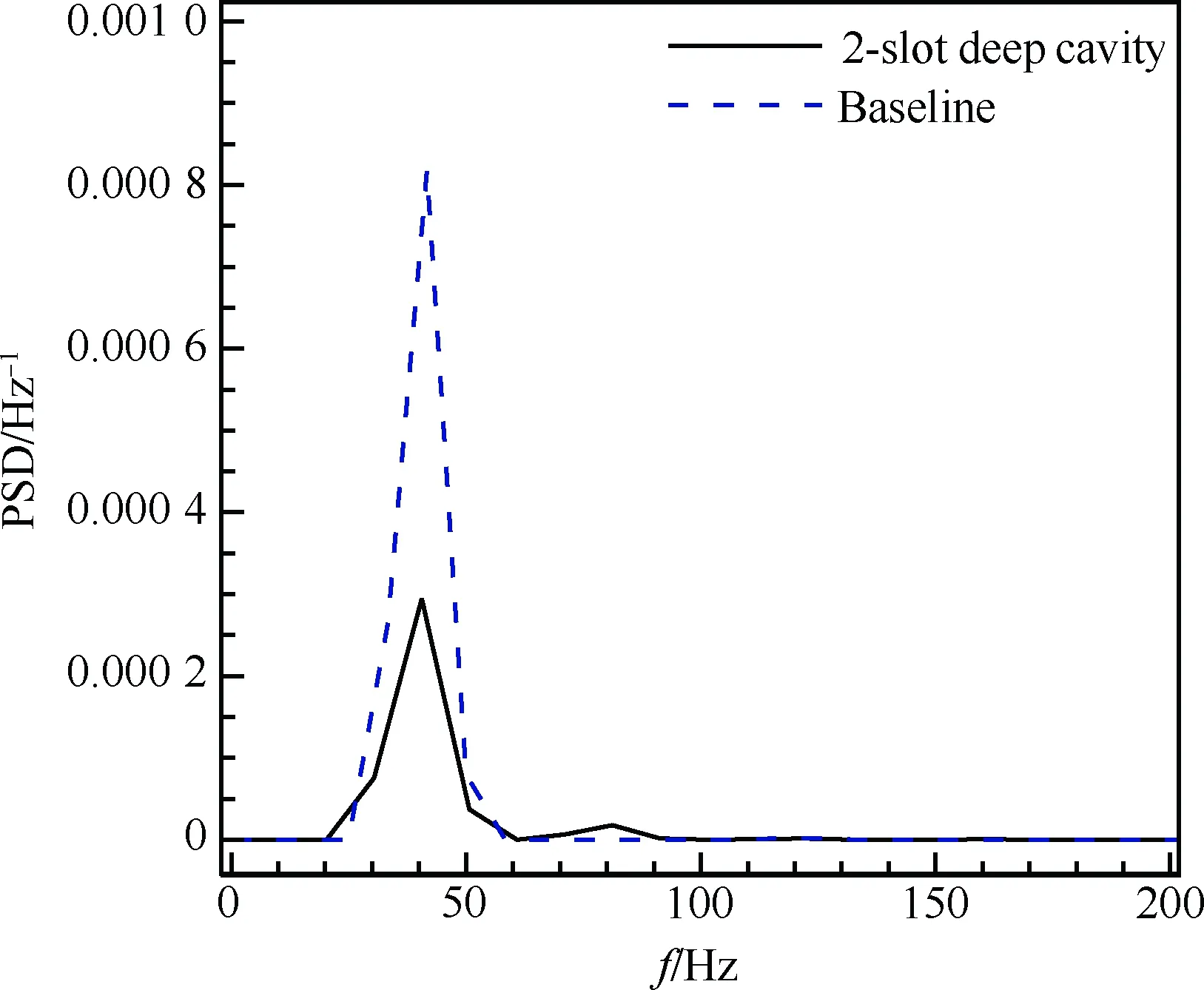
圖16 俯仰力矩系數功率譜密度振蕩比較

Fig.16 Comparison of PSD of pitching moment coefficients oscillations

2.2 空腔深度對激波振蕩的影響

將2.1節中空腔的深度減小一半，其他空腔條件及流動條件均不變，稱為“雙縫半深空腔”(2-slot Half-depth Cavity)。圖18和圖19為采用深空腔和半深空腔兩種措施后的升力系數和俯仰力矩系數與基準翼型的比較，可以看出空腔深度減半，升力系數和俯仰力矩系數振蕩幅值增大，升力系數和俯仰力矩系數上的第二峰值更加尖銳，說明空腔深度的減小使槽縫對流場的干擾增大，但相比于基準翼型，半深空腔情形振蕩幅值還是有所減小。圖20和圖21為升力系數和俯仰力矩系數的功率譜密度圖，可以看出，采用深度減半空腔的翼面上激波振蕩頻率與基準翼型基本是一致的(fbaseline=41.66 Hz,fdeep=40.56 Hz,fhalf-depth=41.67 Hz)。總的來說，將空腔深度減半在減弱激波振蕩方面有一定的效果，但效果不及空腔深度直達弦線的構型。

圖17 開縫空腔翼型上一個周期內不同時刻的馬赫數云圖(Ma=0.76,α=0°,Re=11×106)

Fig.17 Mach number contours at different instants in one cycle on airfoil with slotted cavity (Ma=0.76,α=0°,Re=11×106)

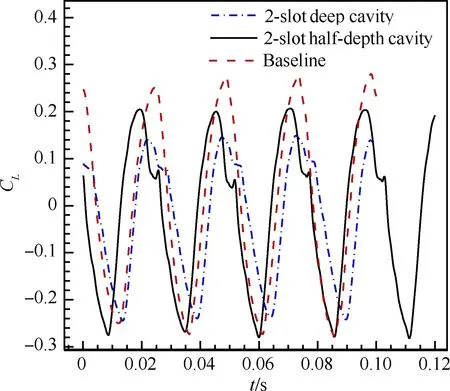
圖18 不同空腔深度下升力系數振蕩比較

Fig.18 Comparison of lift coefficients oscillations with different cavity depths

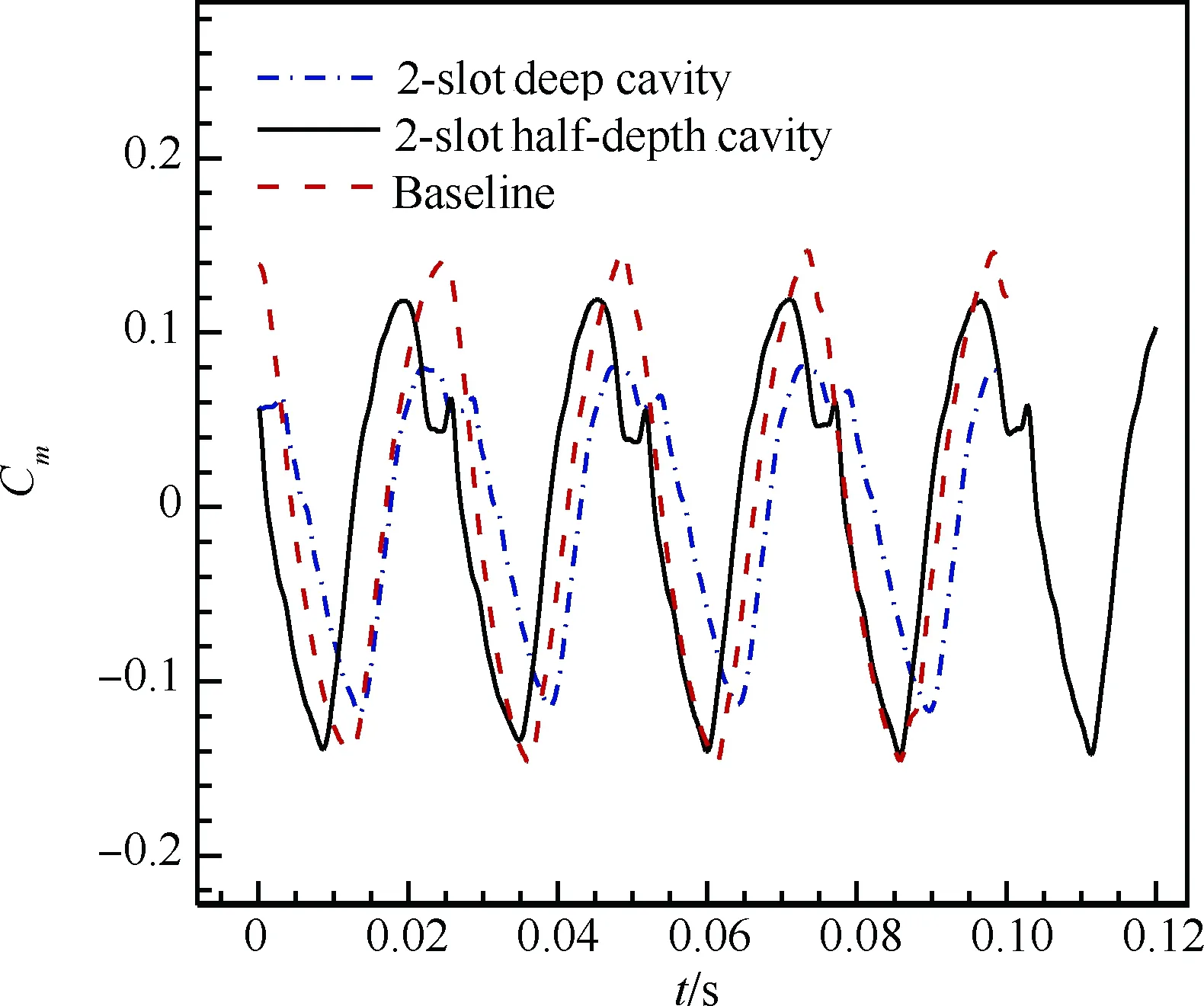
圖19 不同空腔深度下俯仰力矩系數振蕩比較

Fig.19 Comparison of pitching moment coefficients oscillations with different cavity depths

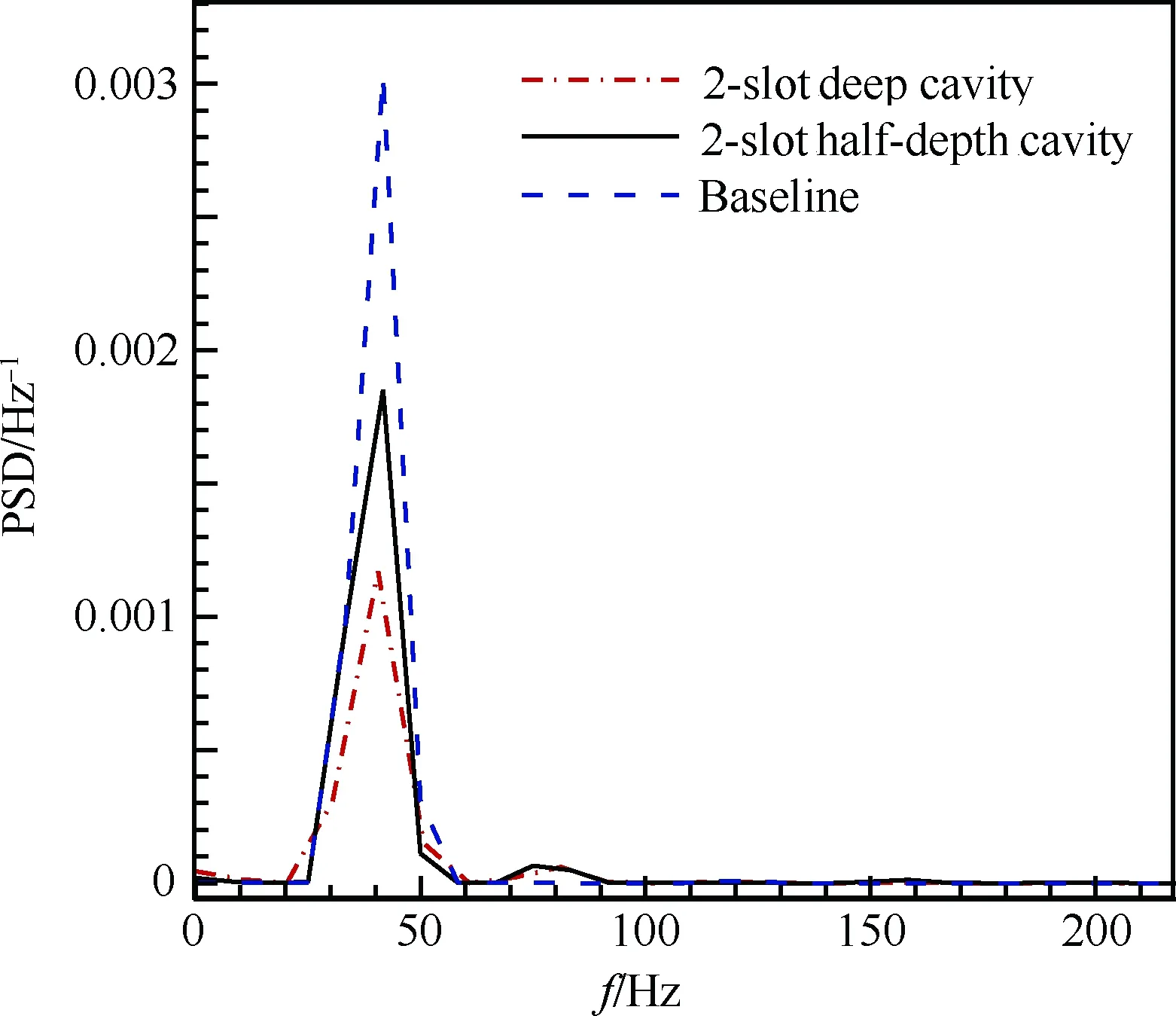
圖20 不同空腔深度下升力系數功率譜密度振蕩比較

Fig.20 Comparison of PSD of lift coefficients oscillations with different cavity depths

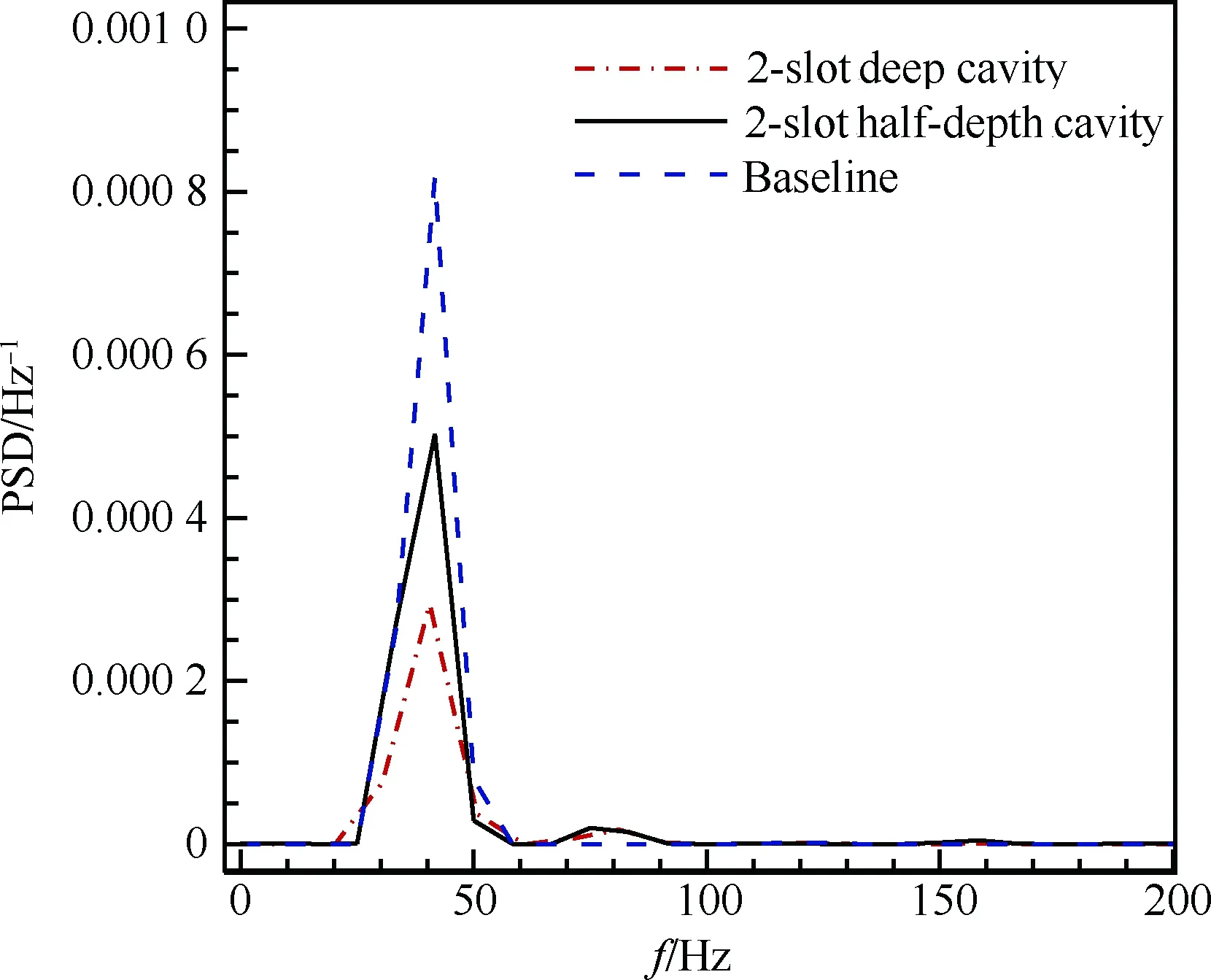
圖21 不同空腔深度下俯仰力矩系數功率譜密度振蕩比較

Fig.21 Comparison of PSD of pitching moment coefficients oscillations with different cavity depths

2.3 開縫數量對激波振蕩的影響

將翼面開縫數量增為3和4，其腔深均直達弦線，稱之為“3縫深腔”和“4縫深腔”，其腔寬、腔深均與2.1節的“雙縫深腔”相同，計算條件也與前兩節一致。圖22和圖23給出了2縫、3縫和4縫深腔的升力系數和俯仰力矩系數隨時間的變化。從圖中看出，3種情況下的升力和力矩系數振蕩相似，且隨著縫數增加，曲線略微上移。圖24 和圖25給出了3種情形下升力系數和俯仰力矩系數對應的功率譜密度，可以看出，3種情形下的抖振頻率基本一致，3縫下的抖振強度比2縫和4縫稍大，2縫和4縫差別比較細微。總的來說，增加開縫數量并沒能更大幅度地減弱抖振強度。

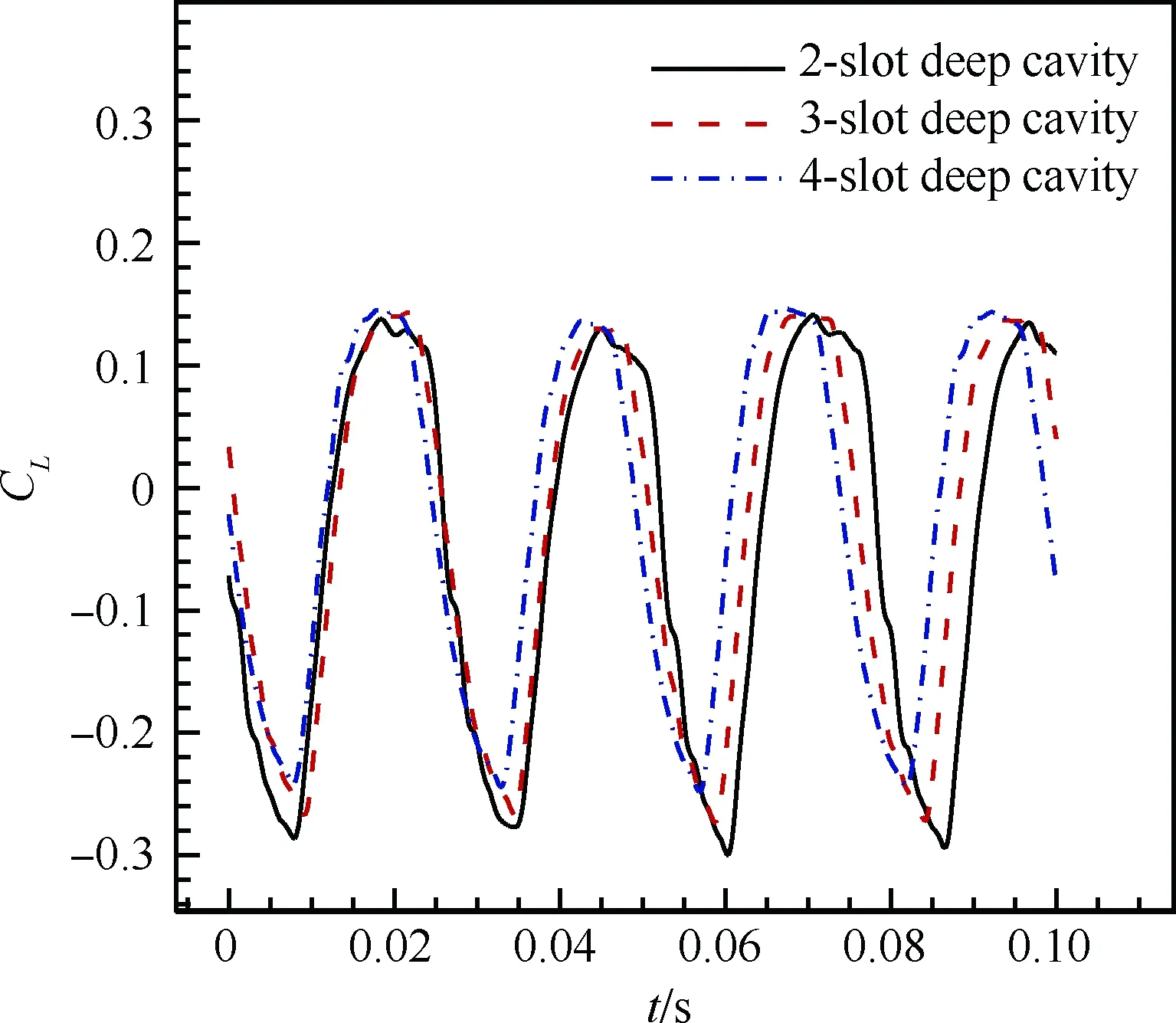
圖22 不同開縫數量下升力系數振蕩比較

Fig.22 Comparison of lift coefficients oscillations with different slot numbers

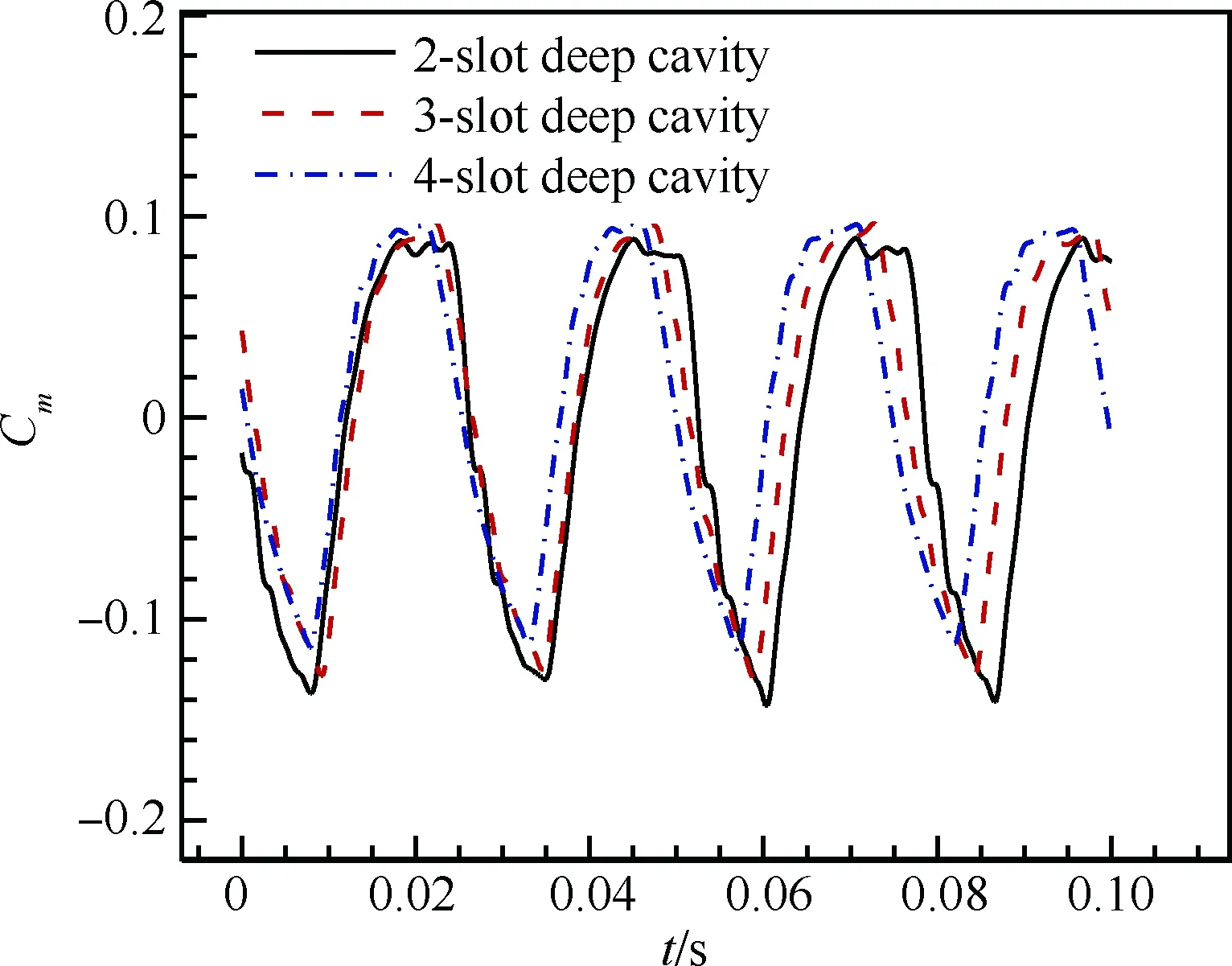
圖23 不同開縫數量下俯仰力矩系數振蕩比較

Fig.23 Comparison of pitching moment coefficients oscillations with different slot numbers

圖24 不同開縫數量下升力系數功率譜密度振蕩比較

Fig.24 Comparison of PSD of lift coefficients oscillations with different slot numbers

圖25 不同開縫數量下俯仰力矩系數功率譜密度振蕩比較

Fig.25 Comparison of PSD of pitching moment coefficients oscillations with different slot numbers

3 結 論

本文通過URANS方法計算了18%雙圓弧翼型的跨聲速抖振，并探討了開縫空腔這一被動控制措施對抖振的抑制效果。

1) 18%雙圓弧翼型的跨聲速抖振中激波只有向前運動而沒有明顯的向后運動。當激波在翼面上運動至其最前的位置后，它退化為弱壓強波，進一步離開翼型以聲波的形式運動到上游流體中；然后又突然出現在它運動所能及的翼面上的最后位置，從而開始新一輪的向前運動，如此形成周期運動。靠近激波平均位置處壓力振蕩最劇烈，3倍弦長尾跡后的壓力已逐漸恢復至來流壓力水平。

2) 在翼型體內開腔并通過2個槽縫與翼型表面通氣可以緩解或抑制抖振(激波振蕩)，但對抖振頻率影響不大。兩縫情形腔深直達弦線的深度比兩縫腔深減半情形抑制效果好，空腔深度變化對振蕩頻率影響不大；腔深均直達弦線時，開2、3、4個槽縫抑制抖振的效果差別不大，3縫情形抖振強度最高，縫數增加時，升力、俯仰力矩系數振蕩曲線略向上平移，開縫數量對抖振頻率影響不大。

[1] TIJDEMAN H. Investigation of transonic flow around oscillating airfoils: NLR TR 77090 U[R]. Netherlands： National Aerospace Laboratory, 1977.

[2] MCDEVITT J B, LEVY L L, JR， DEIWERT G S. Transonic flow past a thick circular-arc airfoil[J]. AIAA Journal, 1976, 14(5): 606-613.

[3] MCDEVITT J B. Supercritical flow about a thick circular-arc airfoil: NASA-TM-78549[R]. Washington， D.C.： NASA, 1979.

[4] LEE B H K. Self-sustained shock oscillations on airfoils at transonic speeds[J]. Progress in Aerospace Sciences, 2001, 37(2): 147-196.

[5] GILLAN M. Navier-Stokes simulation of self-excited shock induced oscillations: AIAA-1995-1809[R]. Reston: AIAA, 1995.

[6] BARTELS R E. Computation of shock buffet onset for a conventional and supercritical airfoil: AIAA-1997-0833[R]. Reston: AIAA, 1997.

[7] RAGHUNATHAN S, GILLAN M A, COOPER R K, et al. Shock oscillations on biconvex aerofoils[J]. Aerospace Science and Technology, 1999, 3(1): 1-9.

[8] DECK S. Numerical simulation of transonic buffet over a supercritical airfoil[J]. AIAA Journal, 2005, 43(7): 1556-1566.

[9] THIEDE P, KROGMANN P, STANEWSKY E. Active and passive shock/boundary layer interaction control on supercritical airfoils: AGARD-CP-365[R]. Brussels: AGARD, 1984.

[10] GIBB J. The cause and cure of periodic flows at transonic speeds[C]//Proceedings 16th Congress of the International Council of the Aeronautical Sciences, 1988: 1522-1530.

[11] CARUANA D, CORREGE M, REBERGA O, et al. Buffet and buffeting active control: AIAA-2000-2069[R]. Reston: AIAA, 2000.

周偉 男， 碩士研究生。主要研究方向： 計算流體力學。

E-mail: 279926870@qq.com

張正科 男， 博士， 教授， 碩士生導師。主要研究方向： 計算流體力學。

Tel: 029-88491224-15

E-mail: zkzhang@nwpu.edu.cn

屈科 男， 博士研究生。主要研究方向： 計算流體力學， 計算海洋動力學。

E-mail: kqu00@citymail.cuny.edu

翟琪 男， 碩士研究生。主要研究方向： 計算流體力學， 流動控制。

E-mail: zhaiqi@mail.nwpu.edu.cn

Received： 2015-03-01； Revised： 2015-03-30； Accepted： 2015-05-04； Published online： 2015-05-13 13:36

URL： www.cnki.net/KCMS/detail/11.1929.V.20150513.1337.003.html

Foundation item： The Preliminary Research Fund of the General Reserve Department of PLA (9140C420301110C42)

*Corresponding author. Tel.： 029-88491224-15 E-mail: zkzhang@nwpu.edu.cn

Numerical simulation of transonic airfoil buffet suppression withslotted cavity

ZHOU Wei1, ZHANG Zhengke1,*, QU Ke2, ZHAI Qi1

1.SchoolofAeronautics,NorthwesternPolytechnicalUniversity,Xi’an710072,China2.DepartmentofCivilEngineering,CityCollege,TheCityUniversityofNewYork,NewYorkNY10031,USA

The unsteady Reynolds average Navier-Stokes (URANS) method is used to compute the transonic buffet, the shock oscillations and the evolution of flow structures of 18% thick biconvex circular-arc airfoil. The suppression effects of passive control with different configurations on transonic airfoil buffet are investigated by numerical method. The computational results reveal that the self-sustained shock oscillation on 18% thick biconvex circular-arc airfoil at transonic speeds has only forward motion without noticeable backward motion. A cavity with ventilating slots, as a passive control measure, can alleviate transonic buffet, but has little influence on the buffet frequency. Deeper cavity has greater effect of suppression but the variation of the cavity depth does not influence the buffet frequency. The suppression effects between 2-slot, 3-slot and 4-slot cavities are insignificant and the number of slots has little influence on the buffet frequency.

transonic; buffet; shock oscillation; cavity; suppression

2015-03-01；退修日期：2015-03-30；錄用日期：2015-05-04； < class="emphasis_bold">網絡出版時間：

時間： 2015-05-13 13:36

www.cnki.net/KCMS/detail/11.1929.V.20150513.1337.003.html

解放軍總裝備部預研基金 (9140C420301110C42)

.Tel.： 029-88491224-15 E-mail: zkzhang@nwpu.edu.cn

周偉， 張正科， 屈科， 等． 開縫空腔抑制翼型跨聲速抖振的數值模擬[J]． 航空學報, 2016, 37(2): 451-460. ZHOU W, ZHANG Z K, QU K, et al. Numerical simulation of transonic airfoil buffet suppression with slotted cavity[J]. Acta Aeronautica et Astronautica Sinica, 2016, 37(2): 451-460.

http://hkxb.buaa.edu.cn hkxb@buaa.edu.cn

10.7527/S1000-6893.2015.0121

V211

： A

： 1000-6893(2016)02-0451-10

*