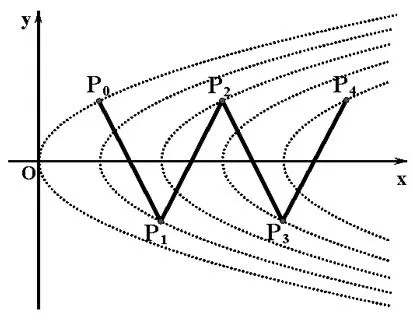
圓錐曲線對定點(diǎn)張直角弦的幾何性質(zhì)研究

?

圓錐曲線對定點(diǎn)張直角弦的幾何性質(zhì)研究

廣東省廣州市番禺區(qū)實(shí)驗(yàn)中學(xué)(511400)潘神龍

我們知道，對圓錐曲線上的定點(diǎn)張直角的弦恒過一定點(diǎn)，這一結(jié)論已散見于各種數(shù)學(xué)刊物，如[1],[2].2011年湖南、2014年山東高考試卷中的解析幾何題目分別涉及了對拋物線、橢圓上的一點(diǎn)張直角的弦的問題，這啟發(fā)我們繼續(xù)對這類問題進(jìn)行研究.特別地，本文重點(diǎn)研究“定點(diǎn)”的幾何性質(zhì).

一、橢圓

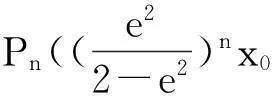
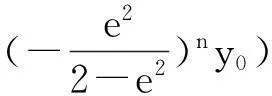
證明：設(shè)lP0M0：y=kx+(y0-kx0)，聯(lián)立后得(a2k2+b2)x2+2a2k(y0-kx0)x+a2[(y0-kx0)2-b2]=0，有

因?yàn)镸0P0⊥N0P0，所以

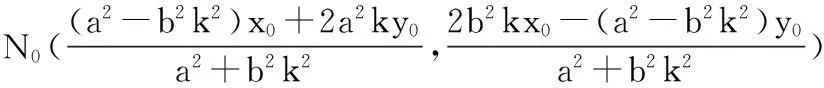
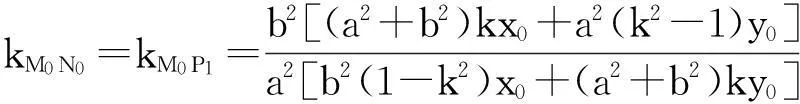
推論1過點(diǎn)P1的弦(P0處法線除外)對點(diǎn)P0張直角.

推論2點(diǎn)P1在P0處的法線上，即任何對點(diǎn)P0張直角的弦都與P0處法線相交于同一點(diǎn)P1.

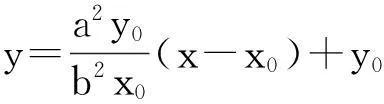
推論3弦M0P0與P0處切線的夾角等于∠N0P0P1，如圖1.

推論4若弦G1G2，H1H2都過點(diǎn)P1，則銳角∠G1P0H1=∠G2P0H2，且SΔG1P0H1∶SΔG2P0H2=tan∠G2tan∠H2，如圖2.

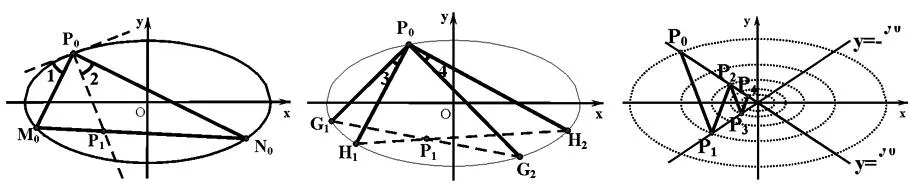
圖1 圖2 圖3

當(dāng)n≥2時(shí)，上述結(jié)果均有類似推廣，并有下面的推論5.

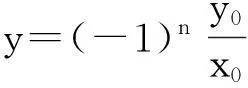
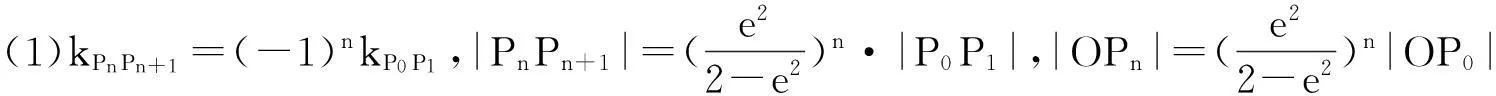
(2)∠PkPk+1Pk+2(k∈)為P0P1與y軸夾角的2倍；

(3)ΔOP0P1～ΔOP2kP2k+1，ΔOP0P1～

ΔOP2k+1P2k+2，k∈.

推論6橢圓Cn與C0離心率相同、特征三角形相似，Cn可看作由C0經(jīng)伸縮變換而成.

二、雙曲線

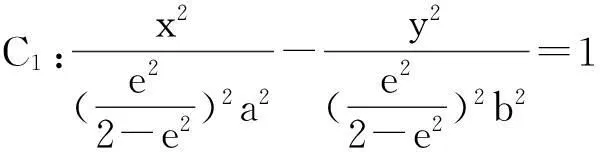
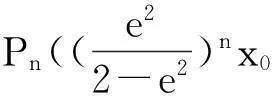
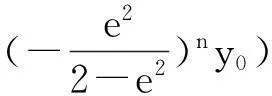
推論1過點(diǎn)P1的直線(P0處法線除外)與C0相交的弦對P0張直角.

推論2點(diǎn)P1在P0處的法線上.

推論3弦M0P0與P0處切線的夾角等于∠N0P0P1.

推論4若弦G1G2，H1H2所在直線都過點(diǎn)P1，則銳角∠G1P0H1=∠G2P0H2，且SΔG1P0H1:SΔG2P0H2=tan∠G2tan∠H2.

長期來看，現(xiàn)有參與者對于區(qū)塊鏈技術(shù)的適應(yīng)和整合程度，是區(qū)塊鏈能否成為平臺、會成為多大平臺的決定性因素。

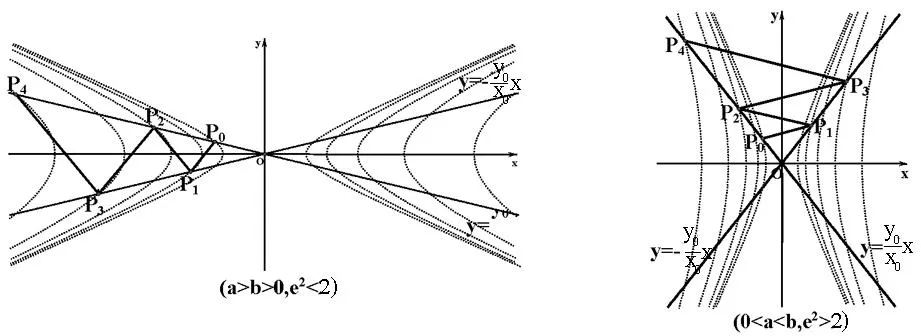
圖4 圖5

當(dāng)n≥2時(shí)，上述結(jié)果均有類似推廣，并有下面的推論5.

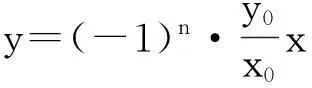
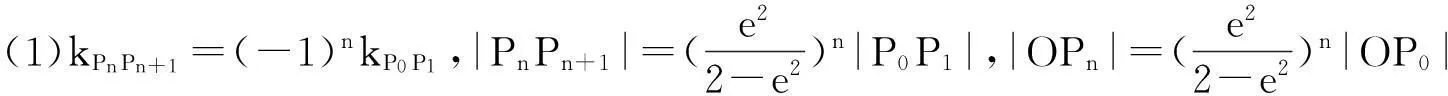
(2)當(dāng)a>b時(shí)，∠PkPk+1Pk+2(k∈)為P0P1與y軸夾角的2倍；當(dāng)a

(3)ΔOP0P1～ΔOP2kP2k+1，ΔOP0P1～

ΔOP2k+1P2k+2，k∈.

推論6雙曲線Cn與C0離心率、漸近線相同、特征三角形相似，Cn可看作由C0經(jīng)伸縮變換而成.

三、拋物線

定理3對拋物線C0:y2=2px(p>0)上定點(diǎn)P0(x0,y0)張直角的弦M0N0上有一定點(diǎn)P1(x0+2p,-y0)；當(dāng)點(diǎn)P0變動時(shí)，點(diǎn)P1所在軌跡為拋物線C1:y2=2p(x-2p)(p>0).類似的，對拋物線Cn-1上定點(diǎn)Pn-1張直角的弦Mn-1Nn-1上有一定點(diǎn)Pn(x0+2np,(-1)ny0)；當(dāng)點(diǎn)Pn-1變動時(shí)，點(diǎn)Pn所在軌跡為拋物線Cn:y2=2p(x-2np)(p>0)，n∈+.

推論1過點(diǎn)P1的弦(P0處法線除外)對P0張直角.

推論2點(diǎn)P1在P0處的法線上.

推論3弦M0P0與P0處切線的夾角等于∠N0P0P1.

圖6

推論4若弦G1G2，H1H2都過點(diǎn)P1，則銳角∠G1P0H1=∠G2P0H2，且SΔG1P0H1:SΔG2P0H2=tan∠G2tan∠H2.

當(dāng)n≥2時(shí)，上述結(jié)果均有類似推廣，并有下面的推論5.

推論5當(dāng)P0不是拋物線的頂點(diǎn)時(shí)，點(diǎn)Pn是拋物線Cn-1在點(diǎn)Pn-1處的法線與直線y=(-1)ny0的交點(diǎn)，{Pn}發(fā)散，滿足：

(1)kPnPn+1=(-1)nkP0P1，|PnPn+1|=|P0P1|；

(2)∠PkPk+1Pk+2(k∈)為P0P1與y軸夾角的2倍.

推論6拋物線Cn可看作由C0向右平移2np個(gè)單位而成.

上述三個(gè)定理可統(tǒng)一敘述為：

參考文獻(xiàn)

[1]張忠旺.圓錐曲線對定點(diǎn)張直角弦的包絡(luò)問題研究[J].數(shù)學(xué)通報(bào)，2013，8.

[2]張定勝.“圓錐曲線的弦對頂點(diǎn)張直角的一個(gè)性質(zhì)”再探[J].數(shù)學(xué)通訊，2007,7:7.