“統計與概率”綜合復習

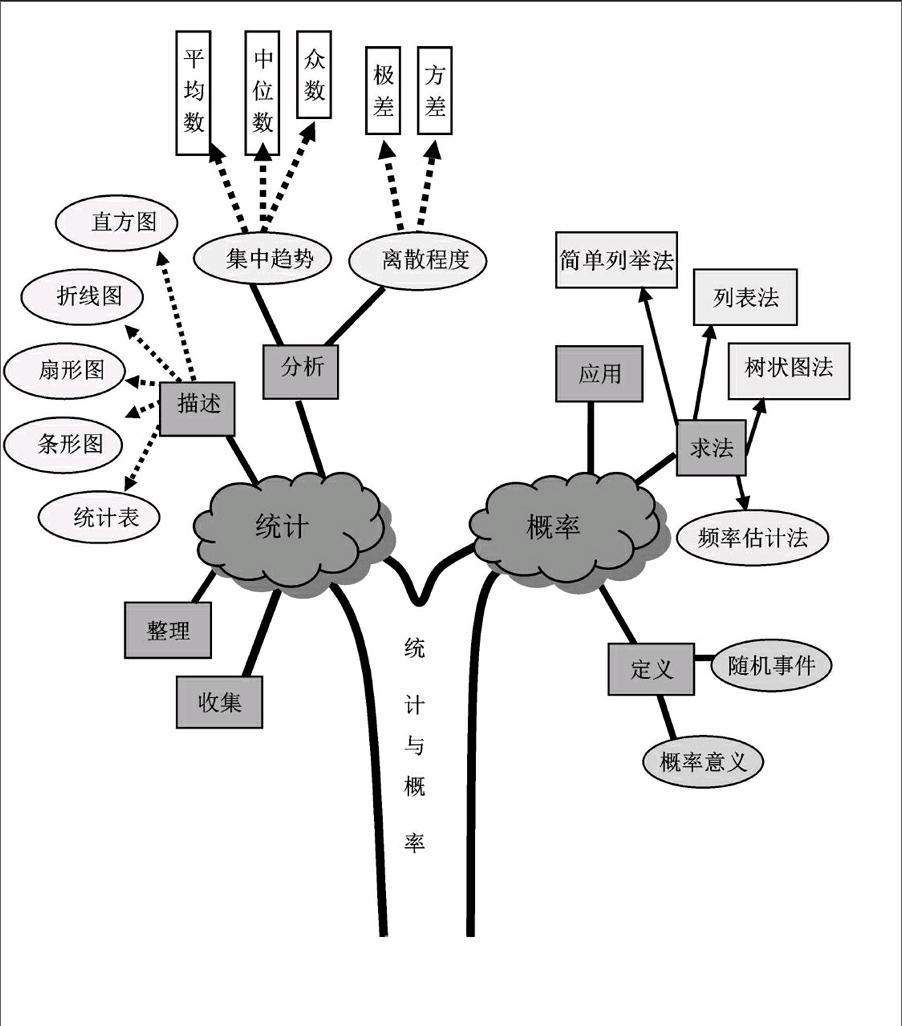
統計與概率在初中學習中占有重要的地位，從七年級教材就逐漸滲透，一直到九年級最后收尾，貫穿三年的學習.近幾年這部分內容在中考中所占的比重也在逐漸增大，與實際生活的聯系也逐漸增多.很多同學在剛剛學習統計概率時，由于對有些概念理解不清，或相關知識的要點把握不到位，或基本思想方法靈活運用不夠，解題時常出現錯誤.現分析幾種常見錯誤供大家參考，在解題中引以為戒.

一、 對統計中基本概念理解不深刻導致錯誤

例1 為了解某校2 000名師生對我市創衛生城市工作知曉情況，從中隨機抽取了100名師生進行問卷調查，這項調查中的樣本容量是（ ）.

A. 2 000名師生對創衛生城市工作的知曉情況

B. 100名師生

C. 100

D. 抽取的100名師生對創衛生城市工作知曉情況

【錯解】樣本容量是指從總體中抽取的樣本數量，所以是100名師生.

【正解】從總體中抽取的樣本個體的數目叫樣本容量，指所要考察對象的數目，不帶任何單位，故選C.

二、 對事件的概念把握不準造成分類錯誤

例2 下列事件中，屬于不確定事件的有（ ）.

①太陽從西邊升起；②從一副撲克牌中任抽一張是紅桃；③擲一枚硬幣，有國徽的一面朝下；④三角形內角和為180°

A. ②③ B. ①③④

C. ① D. ①②④

【錯解】不確定事件是指事件一定不能發生，故選C.

【正解】不確定事件是指事件在發生前，事件的結果不能事先確定，也就是隨機事件，不可能事件是一定不能發生的事件，事件在發生前就能確定結果，它是確定事件.解題中不能把不確定事件與不可能事件混淆，故選A.

三、 對統計圖分析不仔細造成數據看錯

例3 在一次捐款活動中，某班級有50名學生，將所捐款情況統計并制成統計圖，根據圖1提供的信息，捐款金額的眾數和中位數分別是（ ）.

A. 20，20 B. 30，20

C. 30，30 D. 20，30

【錯解】這組數據中，出現次數最多的是20人，故這組數據的眾數為20.中位數是一組數據從小到大排列后，最中間的那個數.這組數據有50個，中位數是第25和26名職工捐款金額的平均數，（30+30）÷2=30，選D.

【正解】眾數和中位數是指調查對象所記錄的數據，不能把數據的個數當作調查的數據.本題是統計捐款錢數，30元出現次數最多，故本題答案是C.

四、 對統計圖意義把握不準造成錯誤

例4 圖2是甲、乙兩戶居民家庭全年支出費用的扇形統計圖.根據統計圖，下面對全年食品支出費用判斷正確的是（ ）.

A. 甲戶比乙戶多

B. 乙戶比甲戶多

C. 甲、乙兩戶一樣多

D. 無法確定哪一戶多

【錯解】一年中乙支出的百分比大于甲支出的百分比，故選B.

【正解】扇形統計圖是為了反映各個部分占總體的百分比，計算各部分的量需用總體與該部分百分比相乘.本題沒有明確甲乙兩家全年的具體收入，所以無法算出食品支出的具體費用，無法比較，故本題正確答案是D

五、 對機會的等可能性理解不夠導致樹狀圖畫錯

例5 在一個不透明的紙箱里裝有紅、黃、藍三種顏色的小球，它們除顏色外完全相同，其中紅球有2個，黃球有1個，藍球有1個，若從中摸出一個球，放回攪勻，再摸另一個球，求兩球顏色相同的概率.

【錯解】畫樹狀圖如下：

可得兩球顏色相同的概率.

【正解】箱中三種顏色的球數目不相同，所以在摸球過程中被摸到的機會是不均等的，本題紅球被摸到的機會大于黃球、藍球，所以在畫樹狀圖時應該把它們轉化為均等機會.正確的樹狀圖如下：

由樹狀圖可得兩球顏色相同的概率為.

六、 對等可能性事件發生的機會和事件最終結果混淆造成錯解

例6 擲一枚硬幣，連擲三次，求有兩次正面向上的概率（ ）.

A. B. C. D.

【錯解】三次拋出的結果分別是：正正正，正正反，正反反，反反反四種情況，其中出現兩次正面向上的情況只有一次，故概率為，選B.

【正解】隨機事件的概率，是把事件在發生過程中所有可能發生的均等機會，與滿足一定條件的機會相比較，不能把事件的最終結果當作機會.正確的解答要通過畫如下樹狀圖：

由樹狀圖可求得兩次正面向上的概率為.

七、 對模擬實驗的條件選擇不合理造成錯誤

例7 端午節，媽媽為洋洋準備了4只粽子：一只香腸餡，一只紅棗餡，兩只什錦餡，4只粽子除內部餡料不同外，其他都相同.洋洋喜歡吃什錦餡的粽子.

在吃粽子之前，洋洋準備用如圖3所示的轉盤進行吃粽子的模擬試驗（此轉盤被等分成四個扇形區域），規定：連續轉動兩次轉盤表示隨機吃兩只粽子，從而估計吃兩只粽子剛好都是什錦餡的概率.轉盤是一個放回的實驗，故第一次轉到什錦（或香腸、或紅棗）后第二次還能轉到.

【錯解】畫模擬試驗的樹狀圖為：

所以有16種情況，其中兩次都是什錦餡的有4種情況，所以概率為.

【正解】設計模擬實驗計算隨機事件的概率，要分清事件的條件，事件發生的方式，事件結果.在設計模擬實驗工具時必須與原事件相關事項保持一致.本題從4只粽子中吃兩只粽子是一個不放回問題，而轉盤是一個放回問題，所以不能以轉盤代替.正確的樹狀圖應該為：

∴P（吃到兩只粽子都是什錦餡）==.

諸如以上常見錯誤，都是同學們在學習過程中不注意把握好基本概念的本質，解題中不注意應用基本方法，解題時分析問題不仔細等一些原因造成的，只要同學們在學習過程中把握好知識的本質要點，解題中分清問題的條件，再加上細心，就可以避免出錯了.

（作者單位：江蘇省宿遷市宿豫區實驗初級中學）