描述數據穩定性的“標尺”

溫靜花

同學們知道用極差描述數據的離散程度簡單明了，但由于極差僅僅由其中的最大值和最小值所確定，個別遠離群體的極端值會在很大程度上影響極差，因而極差往往不能充分反映一組數據的實際離散程度.而方差能非常精確地反映一組數據的離散程度，用方差不僅可以用來解決實際問題，而且還是中考的熱點問題.

一、 直接給出方差，判斷穩定性

例1 甲、乙兩個參加市組織的省“農運會”鉛球項目選拔賽，各投擲6次，記錄成績，計算平均數和方差的結果為：甲=13.5 m，乙=13.5 m，s2 甲=0.55，s2 乙=0.50，則成績較穩定的是_______（填“甲”或“乙”）.

【考點】方差.

【解析】根據方差的定義，方差越小數據越穩定.因為s2 甲=0.55>s2 乙=0.50，方差小的為乙，所以成績比較穩定的是乙.

二、 根據統計圖求解方差，判斷穩定性

例2 甲、乙射擊運動員進行10次射擊，甲的成績是7，7，8，9，8，9，10，9，9，9，乙的成績如圖1所示.則甲、乙射擊成績的方差之間關系是s2 甲_______s2 乙（填“<”，“=”，“>”）.

【考點】折線統計圖，方差.

【解析】由已知，甲的平均成績=（7+7+8+9+8+9+10+9+9+9）÷10=8.5，

乙的平均成績=（8+9+7+10+7+9+10+7+10+8）÷10=8.5，

∴s2 甲=[2×（7-8.5）2+2×（8-8.5）2+5×（9-8.5）2+（10-8.5）2]÷10=0.85，

s2 乙=[3×（7-8.5）2+2×（8-8.5）2+2×（9-8.5）2+3×（10-8.5）2]÷10=1.45.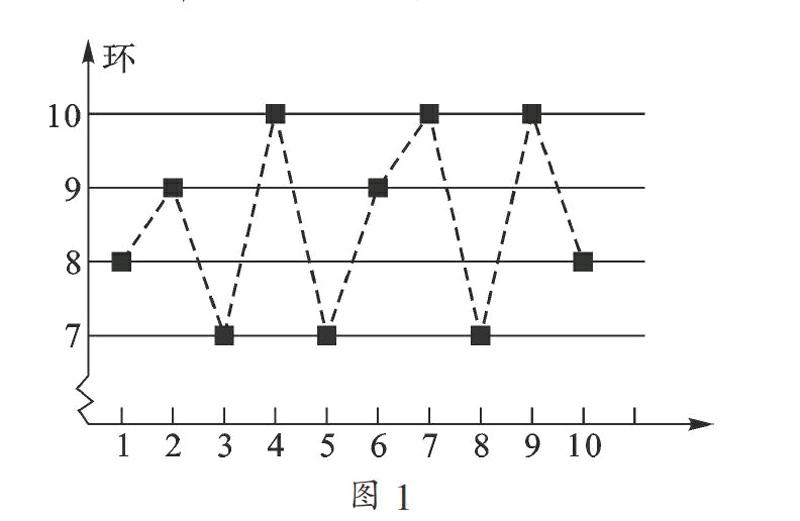

∴ s2 甲

三、 根據統計表求解方差，判斷穩定性

例3 某次跳繩比賽中，統計甲、乙兩班學生每分鐘跳繩的成績情況如下表（單位：次）：

下列三個命題：

①甲班平均成績低于乙班平均成績；

②甲班成績的波動比乙班成績的波動大；

③甲班成績優秀人數少于乙班成績優秀人數（跳繩次數≥150次為優秀）.

其中正確的命題是_______.（只填序號）

【考點】算術平均數，方差，中位數.

【解析】根據平均數、中位數、方差的意義分析三個說法：兩個班的平均成績均為135次，故①錯誤；方差表示數據的波動大小，甲班的方差大于乙班的，說明甲班的成績波動大，故②正確；中位數是數據按從小到大排列后，中間的數或中間兩數的平均數，甲班的中位數小于乙班的，說明甲班成績優秀人數不會多于乙班成績優秀人數，故③正確.故答案為②③.

（作者單位：江蘇省宿遷市宿豫區實驗初級中學）