“多元聯系表示策略”的價值及運用
姜秋萍

【摘 要】在教學中運用“多元聯系表示策略”,對同一或多個數學對象逐步或同時給出多種不同的表征方式,引導學生從不同角度對數學對象加以理解,溝通聯系,可以促進學生對數學概念和數學原理的掌握,促進學生文字、圖表、符號等數學語言的發展。
【關鍵詞】多元聯系表示策略;價值;運用
所謂“多元聯系表示”策略,就是利用數學對象表征形式的多樣性,對同一或多個數學對象(數學的概念、法則、表達式、定理、定義等)逐步或同時給出多種不同的表征方式(圖、表、文字或符號等),引導學生從不同的角度加以理解,溝通其聯系,從而促進學生數學語言發展的策略。
一、多元聯系表示,促進學生對數學概念語言的掌握
運用用概念“多元聯系表示策略”可以有效地幫助學生掌握數學概念語言。概念是思維的基本單位,數學概念是人類對現實世界的空間形式和數量關系的簡明、概括的反映,是具體性與抽象性的辨證統一。有大量實在屬性的概念問題,比缺乏實在屬性的概念問題更加容易解決。這意味著在問題情境中,為提取概念所提供的線索越多,就越容易使概念得到檢索和應用。給抽象的概念建立起具體的模型,更有利于學生對概念的掌握。比如給分數概念配以不同的模型解釋或實際情境解釋,學生將比較容易而且牢固地掌握分數的概念。
案例:三年級上冊《認識分數》
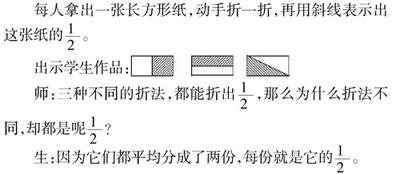
每人拿出一張長方形紙,動手折一折,再用斜線表示出這張紙的。
出示學生作品:
師:三種不同的折法,都能折出,那么為什么折法不同,卻都是呢?
生:因為它們都平均分成了兩份,每份就是它的。
在這樣的情境中,數形結合,給抽象的概念建立起具體模型。學生可以在把握數學對象不同方面的基礎上,將不同表示法中所蘊涵的信息組合在一起,相互轉換,這就大大增加了建立數學對象不同方面的聯系性,促進學生對數學概念語言本質的掌握。
二、多元聯系表示,促進學生對數學原理語言的理解
數學命題中的定理、公式、法則等,我們將它稱之為數學原理,數學原理的學習實質是數學概念之間關系的學習。數學概念之間聯系的方式,主要有兩種:一種是相似和差異,一種是包含。基于相似和差異的聯系方式中,最重要的就是“多元聯系表示”思想。數學原理是一種高度復雜性的數學語言,認識心理學認為,要理解性地學習一個數學原理,必須通過建立該原理與已有認知結構的相關知識之間的聯系,將它納入到自己已有認知結構中的恰當位置。多元聯系表示策略,就是充分利用知識之間的相似性,通過多元聯系表示,溝通知識間內在聯系,促進知識的生長、擴張和加強,從而促進了學生對數學原理語言的理解。
案例:六年級上冊《比的基本性質》
師:比、分數、除法有什么關系?
(學生語言敘述,師摘錄成圖表語言形式,見下表。)
師:我們以前嘗過商不變的規律和分數的基本性質,聯想這兩個性質,想一想,比會有什么樣的性質?
(引導學生由商不變的性質、分數的基本性質、比與它們的聯系總結得出比的基本性質。)
三、多元聯系表示,促進學生三種數學語言的發展
數學語言是一種抽象的專業語言,是一種特殊語言,可以分為文字語言、圖表語言和符號語言。三種數學語言各有優勢與不足:文字語言通俗、易懂,但描述起來是線性的,不易表露知識的內在結構;數學符號十分簡潔,描述起來給人以結構感,便于抽象思維,但由于抽象程度高,不易理解;圖表語言比文字語言和一般符號語言更具直觀性,容易形成表象,便于形象思維。“多元聯系表示策略”,就是基于數學語言表示的多樣化,在數學思維中,發揮文字語言、圖表語言和符號語言的優勢互補作用,將三種數學語言有機融合,促進了學生三種數學語言的發展。
四、多元聯系表示策略的運用,要遵循合理認知原則
“多元聯系表示”策略的應用確實可以提高學生對數學對象的理解,數學語言的掌握,但是“多元聯系表示”并不一定能帶來好的學習效果,“多元聯系表示”也要遵循合理認知原則,適量而恰當,以減輕認知負擔,增強認知效果。
一是適量。心理學研究表明,學習者對教學內容本身所包含的信息元素的數量及其交互性進行認知加工要承受一定的認知負荷。如果教學中多元聯系的元素太多,而且元素的交互性很強,就會產生冗余效應,增加學生學習的負擔,引起學習困難。比如概念的教學,向學生提供數量較多的具體事例,可以便于學生對概念的各種要素進行全面鑒別,抽象出概念的本質。但是這種事例太多的話,概念的非本質屬性將有可能被強化而掩蓋概念的本質。在教學中如果單一或較少的信息可以呈現完整且明確的信息意義,則可以獨立呈現,無需呈現多種形式。
二是恰當。也就是指教學中的“多元聯系表示”呈現的材料要恰當,如果不恰當,會產生與學習者認知加工過程沒有直接關聯的活動,導致不必要的或無意義的認知操作,會增加學生的認知負荷或把學習者引向偏離學習主題的心理活動。比如學生剛接觸有關概念時,教師如果不恰當地呈現反例,使概念的無關特征得到不必要的強化,從而干擾對概念的理解。
總之,“多元聯系表示策略”的運用可以極大地拓展數學學習空間,有力地支持教學活動,有利于引導學生開展高水平的、深層次的數學思維活動,使學生自主探究式學習成為可能并得到落實,學生的數學學習興趣可以被有效的激發,從而使教學生動活潑而富有成效,促進學生的數學語言發展。

