巧構圖形 一石三鳥

陸祥雪

本文試圖從初中銳角三角函數的定義出發，利用一幅圖形，證得兩角和的正切、正弦、余弦公式，以展示用圖形演繹數學知識的力量.

一、圖形構成

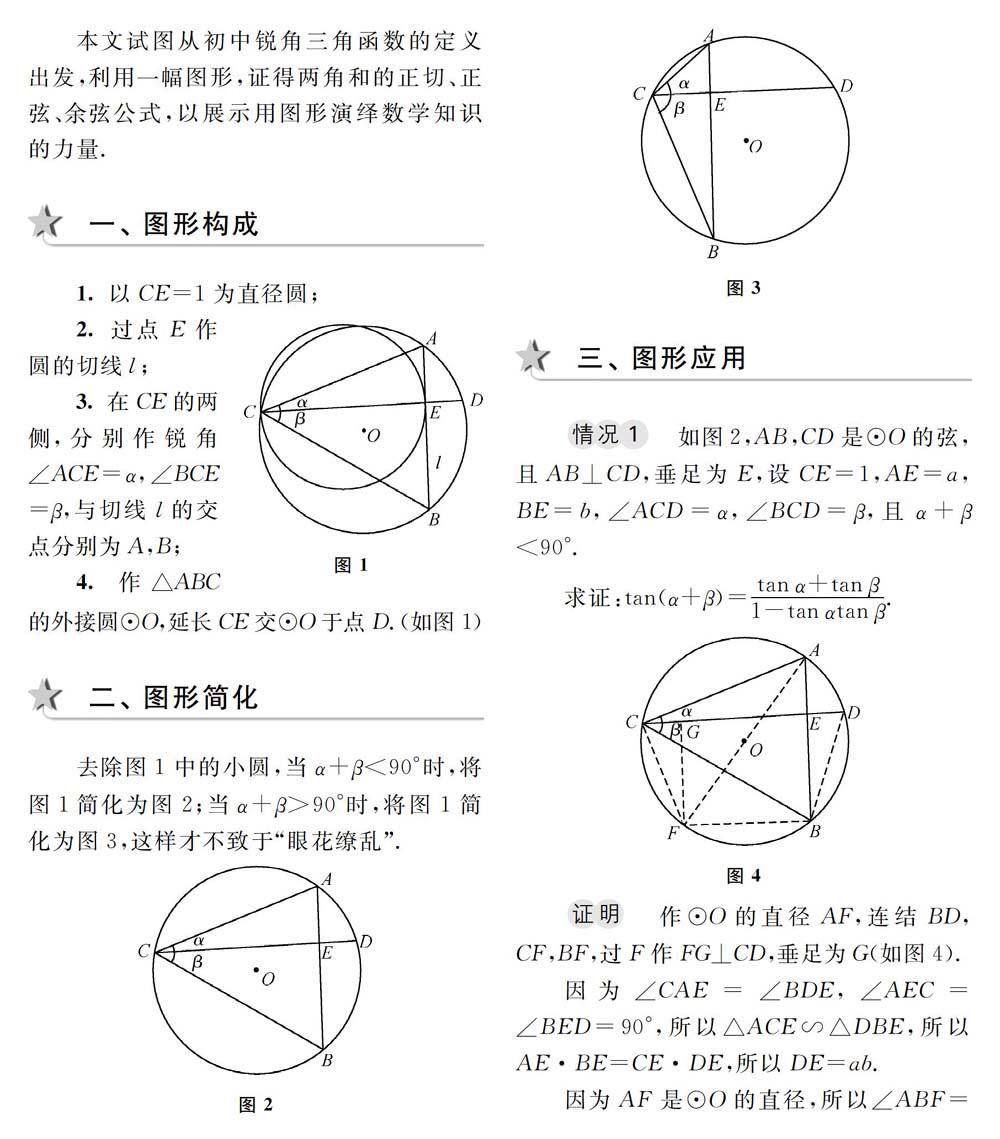
1.以CE=1為直徑圓；

2.過點E作圓的切線l；

3.在CF的兩側，分別作銳角∠ACE=α，∠BCE=β，與切線Z的交點分別為A，B；

二、圖形簡化

去除圖1中的小圓，當a+p<90°時，將圖1簡化為圖2；當α+β> 90°時，將圖1簡化為圖3，這樣才不致于“眼花繚亂”.

三、圖形應用

當α+β>90°時，在圖5的基礎上一樣可以解決.對α+β 90°的情形，我們只要代人驗證就OK了.

利用圖2、3，能證明兩銳角和的余弦公式嗎？回答是肯定的，您不妨一試！

至此，我們利用圖1及其兩種分類情形，分別推證出，當α，β為銳角時，這兩角和的正弦、余弦、正切的公式.這再一次讓我們體會到了數學的博大精深.