X—R控制圖在瀝青混合料生產質量控制中的應用

王同++李思李++田波

摘要：通過對瀝青拌和站中瀝青用量數據的統計分析，表明瀝青用量在瀝青混合料生產過程中存在波動性和規律性，運用統計學的方法對瀝青用量進行分析，繪制了控制圖，并對其進行修正，使其可以有效的對瀝青拌和站的運行狀態進行控制，保證瀝青混合料生產環節的質量。

關鍵詞：瀝青混合料；質量控制；波動性；控制圖

中圖分類號：U414

文獻標志碼：B

引言

利用統計學原理對瀝青混合料大量生產數據進行分析的結果表明，質量監測數據一般存在波動性和規律性兩方面的性質。

正態分布是統計學中最重要、最基本的一種分布形式。對于質量控制，要求施工質量l00%滿足性能要求，在大多數情況下是不可能實現的，只要控制指標值滿足一定的保證率，就認為質量控制的結果是可以接受的。

在統計質量管理中，控制圖作為一種重要的工具，是由美國休哈特博士于1924年創立的，他將數理統計方法引入，開始了統計質量控制的階段。控制圖由正太分布曲線演變而來，因此，運用控制圖進行施工過程的質量控制能有效地控制工程質量的同時，也能科學地評價施工水平的高低。

1 數據波動性與正態性

1.1 波動性

根據對質量的影響程度，在數理統計上，把影響質量波動的因素分為偶然因素和系統性因素兩大類。當過程僅受偶然因素影響時，過程處于統計控制狀態（簡稱受控狀態）；當過程中存在系統因素的影響時，過程處于統計失控狀態（簡稱失控狀態）。

以拌和樓數據庫中的瀝青用量為例，圖l為瀝青實際用量與最佳用量的關系圖，由該圖可以看出，瀝青的實際用量在最佳用量附近波動。

標準偏差σ可以反映樣本的絕對波動狀況，但當測量樣本平均值不同時，只使用標準偏差不能完全反應出數據的波動性，因此用相對波動的大小，即變異系數更能反映樣本數據的波動性。

變異系數是瀝青路面動態控制中非常重要的特征量，表示數據相對波動的大小，也就是相對的分散程度，用Cv表示式中：σ為所測樣本的標準偏差；X為所測樣本的均值。

在施工質量管理中，應盡量減小瀝青含量變異的大小，將瀝青含量的波動性控制在一定范圍內，減小其變異系數。

以每4盤瀝青用量為l組進行統計，求得每組瀝青用量的變異系數，結果見表l。由表l看出，樣本組8、9、13的變異系數超過了3%，說明這2組數據的波動性較大，瀝青用量的數據存在可疑，應檢查設備是否出現問題。

1.2 正態性

上文提出，產品質量是存在波動的，但并不是說這種變動不可預測，無章可循。根據統計學理論，對數據進行數理統計分析，就可以找出質量波動的幅度，以及不同波動幅度出現的概率，這就是質量變異的統計規律。

正態分布通常只在區間（μ-3σ，μ+3σ）內研究正態總體的分布情況，只要質量檢測值落在該范圍內，則認為該結果是可以接受的；如果控制指標超過此范圍時，應立即停工調整，直到恢復正常。

以拌和樓數據庫中的瀝青實際用量數據為例，將瀝青實際用量進行統計，由圖2可以看出，瀝青實際用量呈現正態分布規律，因此可以使用正態分布的相關結論，對瀝青路面施工進行質量控制。

2 休哈特控制圖

從控制圖的變化趨勢中判斷生產過程是否處于穩定狀態的方法，將產品質量控制從事后檢驗改變為事前預防，這為保證產品質量、降低生產成本、提高生產效率開辟了廣闊的前景，因此控制圖在世界各國得到了廣泛的應用。目前，均值控制圖和極差控制圖即X-R控制圖通常用于瀝青路面施工過程質量控制。

2.1 控制圖原理

對于質量管理，正常情況下可以認為檢測值服從于正態分布。如果忽略數據監測時的隨機誤差，在不產生系統偏差的情況下，隨機抽樣后測定的質量特征應滿足下式

Xi～N（μ，σ） i=ι，2，…，n

（1）

因此根據正態分布的3σ原理，均值μ與標準差σ的取值多少，最終產品質量特性值Xi落在（μ3σ，μ+3σ）區間的概率為99.73%；而產品質量特征值的取值超出[μ-3σ，μ+3σ]范圍的可能性為0.27%，大于μ+3σ或小于μ-3σ的概率為0

休哈特利用以上特性，取[μ-3σ，μ+3σ]范圍作為控制界限構造了控制圖，稱為休哈特控制圖，其中包括中心線（CL線）、控制上限（UCL線）、控制下限（LCL線）三條控制線。

2.2

X-R控制圖

在X-R控制圖中，中心線為控制指標的平均值；UCL線與LCL線分別為控制指標的上下控制界限，數據在該范圍內波動屬于正常狀態。一旦被測數據落在該區域外，說明此時該項指標出現異常，為保證施工質量的穩定，應及時采取措施進行處理，避免系統出現大的問題。因此不難理解，若控制上下限范圍越小，說明施工水平越高，數據變異性或波動性越小；反之亦然。

在X控制圖中

同理，R控制圖的控制界限為

式中：CL-X為R控制圖中心線，某階段指標檢測結果平均值；UCL-X為R管理圖中的質量控制上限；LCL-X為R管理圖中的質量控制下限；x為每組平均值X的平均值；σR為極差R的方差；R為每組極差R的平均值；d2、d3、A2、D3、D1為系數，其大小可根據樣本大小n計算3σ控制界限參數表得到。

應用控制圖進行質量控制最主要目的是判斷某一生產過程是否處于穩態或者可控狀態。根據數理統計計算可知，判斷過程處于穩態有以下三個準則。

（l）控制圖中連續25個點子落在UCL線與LCL線之間。

（2）控制圖中連續35個點子中，最多出現1個點子落在UCL線與LCL線之間之外。

（3）控制圖中連續lOO個點子中最多出現2個點子落在UCL線與LCL線之間之外。endprint

三條準則對應不同數量的測試數據。

3 實例分析

上文介紹了控制圖的基本原理以及休哈特控制圖的計算過程，本節以瀝青用量為例，探討利用統計學中平均值 極差控制圖對關鍵參數進行控制的方法。

通過瀝青混合料數據采集系統，對一段時間內拌和樓的生產數據進行監控，針對瀝青用量抽取了200個數據進行分析，每組樣本大小為4，共分成了50組，每組數據的平均值X與極差R值，詳見表2。

根據2.2節所提供的公式計算X控制圖與R控制圖的控制界限：對于X控制圖，由式（2）、（ll）、（12）得CL=141.741.UCL=144.768，LCL=138.714。

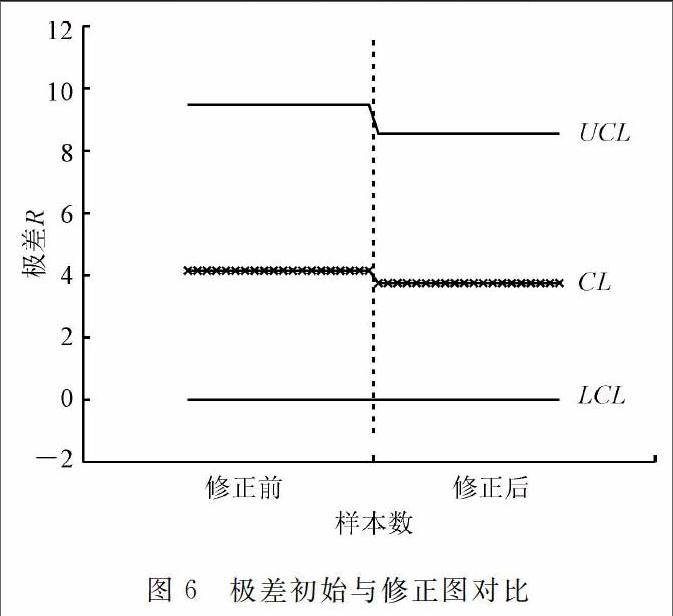
對于R控制圖：由式（5）、（13）、（14）得CL=4.152，UCL=9.475，LCL=O。

系數可按計算3σ控制界限參數表取值，其中：A2=0.7289，D3=0，D4=2.282。

將樣本數理統計量X和R逐一描點在圖上，用折線連接，得到XR控制圖，如圖3、4所示。

由圖3、4中樣本點狀態可以看出以下幾點。

（l）X控制圖中第7號樣本點超出上控制線。

（2）極差R控制圖中第8、9、l3、38號樣本點超出上控制線。

（3）X控制圖中處于控制界限內的樣本點基本平均分布在中心線附近。

（4）極差R控制圖中處于控制界限內的樣本點多數在中心線下方。

經過確定，7、8、9、38號樣本超出上控制線為系統穩定性原因所引起的，刪除這些樣本之后重新確定控制界限。

首先按以下公式計算

式中：Xd為剔除樣本后的平均值；md為剔除的樣本組數；Rd為剔除一組的極差；m為原有的樣本組數。

計算得

對于X控制圖修正后的控制界限，由式（2）、（ll）、（12）得：CL=141.67， UCL=144.402， LCL=138.936。

對于R控制圖，由式（5）、（13）、（14）得：CL=3.75，UCL=8.555， LCL=O。

圖5、6為修正前后控制圖變化情況，由該圖可以看出修正后控制圖的中心線下移，控制界限變窄，說明控制水平得到提高。

經過修正的控制圖在使用過程中都要經過不斷改進，以保證每個階段均處于可控狀態，要提高控制的質量水平，其關鍵是預防和糾正措施。當認為控制的目的基本達到后，可不必繼續修正控制圖，而是進行定期抽樣檢測以檢測是否保持現有狀態即可。

4 結語

本文以拌和樓的瀝青用量數據進行了數據波動性分析并運用控制圖的方法進行了統計分析，可以有效的對拌和樓的運行狀態進行控制。因此在瀝青混合料生產過程中建立基于概率統計的質量控制體系，可以客觀全面地檢測評價路面施工質量，為施工質量控制提供基礎數據，并為工程驗收和實施按質支付提供依據。endprint