平移在數學解題中的妙用——由一道中考壓軸題的解法聯想到

☉福建省莆田中山中學　陳荔清

?

平移在數學解題中的妙用——由一道中考壓軸題的解法聯想到

☉福建省莆田中山中學陳荔清

俗話說：“要給學生一杯水，教師要有一桶水.”但是，如果教師有了一桶水，那么倒給學生那杯水時，怎樣倒不至于把水倒出杯外？就要講教學方法，即需要教學的藝術.

現在有些老師在初中總復習時，為了對付中考的“壓軸題”，成了歷年全國各地中考壓軸題的“搬運工”，把原題中的解答過程不假思索地拋給學生，使學生負擔重，收效甚微，而且還不得要領.從這個意義上來講，我們在數學總復習時對壓軸題的解答要作一番分析和思考.凡是要給學生講的或讓學生做的題，我們教師一定要去做一遍，這樣不但能提高教堂效果，而且能“教學相長”，提高自身的水平.

在數學教學中，“一題多解”能夠調動學生學習的積極性.從“多解”中尋求解決問題的一般規(guī)律，讓學生理清思路，掌握方法，運用它來“舉一反三”，解決其他類似問題，這才是我們要求的目標.

題目已知線段OA⊥OB，點C為OB的中點，D為線段OA上一點，連接AC、BD交于點P.

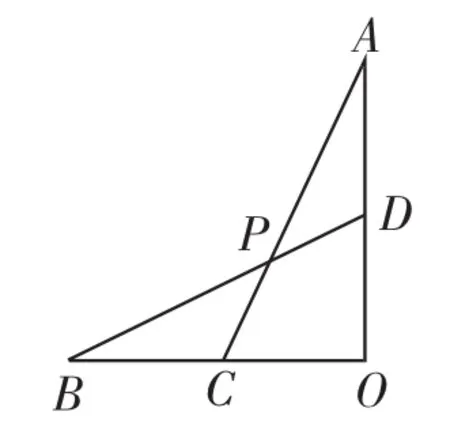
圖1

圖2

圖3

解答過程：問題（1）是特殊位置驗證，筆者用以下兩種較通俗方法證明.

方法一：如圖4，中線倍長：過點A作AH⊥AD交BD延長線于點H.

證△ADH≌△ODB，得BO=AH.

因為BO⊥AO，所以AH∥BO.

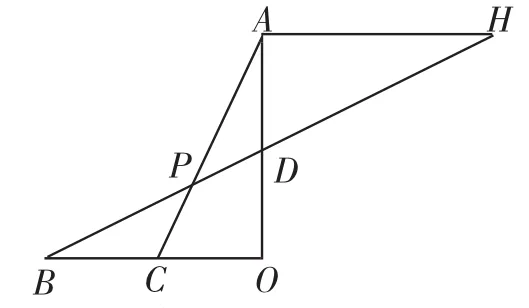
圖4

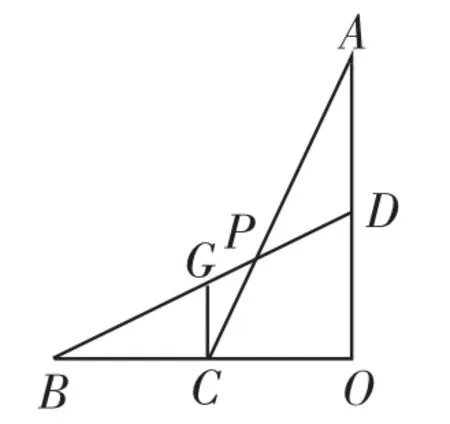
圖5

方法二：如圖5，過點C作CG∥AO交BD于點G，

因為AD=OD，

思路點撥：本題所要求的結論是線段比值，問題一定要轉化為相似或平行線分線段定理，以下用6種方法解答問題（2）.

方法一：設AD=a，則AO=BO=4a.如圖6，過點A作AH∥BD且BH∥AO，連接CH，則四邊形ADBH為平行四邊形.

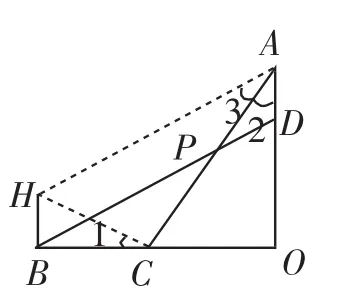
圖6

所以△BHC∽△OCA，所以∠1=∠2.

可證△ACH為Rt△，

方法二：如圖7，過點D作DF∥BO交AC于點F，

因為DO=3a，BO=4a，所以BD=5a，所以DP=a=AD，

所以∠2=∠A，

所以∠BPC=∠A，

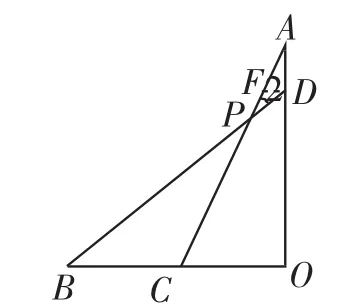
圖7

圖8

方法三：如圖8，過點B作BE⊥AP交AP延長線于點E，設AD=a，則AO=BO=4a，可證△BCE∽△ACO.

方法四：如圖9，過點D作DF∥AC，過點C作CF∥AO 交DF于點F.

則四邊形DACF為平行四邊形，所以∠A=∠F.

設CF=AD=a，則BD=5a.

因為DP=CF=a，

所以四邊形DPCF為等腰梯形.

所以∠F=∠PDF，∠BPC=∠PDF.

圖9

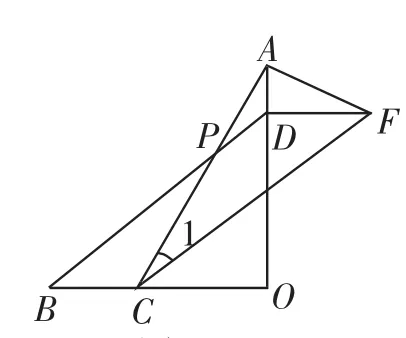
圖10

方法五：如圖10，過點C作CF∥BD，且DF∥BO，

則四邊形DBCF為平行四邊形.

所以∠BPC=∠1.

設AD=a，則OD=3a，

所以△ADF∽△FAC，所以∠CAF=90°.

∠1=∠AFD=∠BPC.

方法六：如圖11，過點D作DF∥BD，CF∥AD交DF于點F.

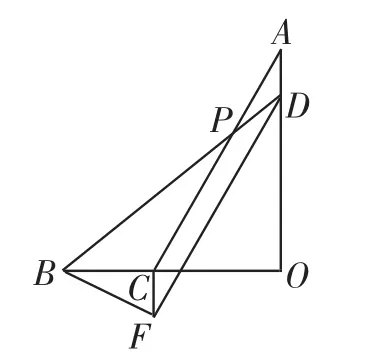
圖11

連接BF，則四邊形CFDA為平行四邊形，

所以∠A=∠CFD，所以∠BCF=∠AOB=90°.

設AD=a，則BC=CO=2a，CF=AD=a，

可證△BCF∽△AOC.

所以∠A=∠FBC=∠CFD，∠BFC=∠ACO.

所以∠BFD=∠BFC+∠CFD=∠BFC+∠FBC=90°.

本題考查的問題是平行四邊形、相似三角形、三角的綜合應用.運用一題多解進行全方位的展示拓展，讓同學們從這精彩紛呈的解法中提高解題的興趣.樹立學好數學的信心，提升解題能力.