多組元混合物狀態方程*
施研博,趙艷紅,劉海風,孟續軍,王學容
(北京應用物理與計算數學研究所,北京 100094)
1 引 言
在高能量密度物理領域,常常會遇到因多介質、流體力學不穩定性等導致的物質混合,對此類現象進行流體力學或輻射流體力學模擬時,需要混合物的狀態方程。在很多情況下,構成混合物的單質狀態方程已知,而混合物的狀態方程難以直接獲得,此時采用等溫等壓條件及體積相加原理可以得到混合物的狀態方程。徐錫申等人[1]指出:采用體積相加模型和等溫等壓假設,可以計算化合物、混合物及合金的狀態方程;對于實際的物態方程,模型給出的方程組形式復雜,難以求解,可采用作圖法計算混合物的分密度。然而,徐錫申等人并未給出具體的計算模型。王正言等[2]、唐鴿等[3]、王學容等[4]采用等溫等壓的熱力學平衡條件和體積相加原理,針對兩組元混合情況,計算了混合物的壓力、內能和定容比熱容。Cranfill[5]也給出了壓力平衡、溫度不一定平衡時混合物狀態方程的計算方案,但是未給出熱力學量的具體求解方法。
在實際工作中往往會遇到多于兩種組元混合的情形,而且除了壓強、內能和定容比熱容外,有時還需要壓強系數、等熵聲速等其他熱力學量。本工作基于等溫等壓的熱力學平衡條件和體積相加原理,給出多組元混合物狀態方程的理論模型,由此求解組元分密度及混合物的熱力學量;采用該模型計算一種4組元鎢合金的狀態方程,并與其他理論計算結果進行對比,驗證模型的有效性。
2 理論模型
在實際工作中,我們感興趣的是物質在高溫、高壓狀態下的性質。首先,假定混合物中各組元之間沒有發生化學反應,從而能夠很好地滿足原子的體積相加原理[1];其次,假定混合物中各組元之間達到熱力學平衡,溫度、壓力處處相等。由此可以求得各組元的分密度,進而求得混合物的熱力學量。
2.1 組元分密度
考慮單位體積的混合物,記混合物的密度為ρ,第k種物質的質量為mk,分密度為ρk,第k種物質的質量比定義為wk=mk/ρ。根據假設,混合物與各組元之間滿足體積相加原理,得到
式中:n為組元數。由混合物各組元間的溫度和壓力相等假設,可知
聯立求解n個方程,可以得到混合物各組元的分密度ρk。
2.2 熱力學量求解
比內能e和定容比熱容cV分別為
其中{(?ρl/?T)ρ}可由n個方程聯立求解
(7)
式中:k=1,2,…,n-1。
由等溫等壓假定,混合物的壓強p、壓強系數β和等溫聲速cT可以通過第k種組元的壓強求解
其中{(?ρl/?ρ)T}也由n個方程聯立求解
式中:k=1,2,…,n-1。
根據熱力學關系,由等溫聲速可得到等熵聲速cS
至此,所需的熱力學量計算完畢。所有熱力學量都是由基本的熱力學定律和關系式導出,自然滿足熱力學自洽性及穩定性條件[2]。
3 計算結果
編制了多組元混合物狀態方程計算程序,計算了由4種組元構成的鎢合金(W89Mo9Fe1Ni1)的狀態方程。單質狀態方程采用寬區實用狀態方程[1]提供的狀態方程庫,該庫還提供了鎢合金W89Mo9Fe1Ni1的狀態方程。
鎢合金W89Mo9Fe1Ni1的沖擊雨貢紐曲線如圖1所示,圖中比較了計算得到的狀態方程與狀態方程庫給出的合金狀態方程,其中ρ0為常壓密度,TH為沖擊雨貢紐溫度。從圖1可以看到,兩種狀態方程得到的壓強和沖擊雨貢紐溫度具有很好的一致性。進一步比較由兩種狀態方程得到的沖擊壓力的相對差異(Δp/p),如圖2所示。可以看到:在常密度附近,Δp/p最高達到6%,這是由于在常溫常密度狀態附近,合金各組元的體積與體積相加假設偏離較大;在我們感興趣的壓縮區,Δp/p降到2%以下。
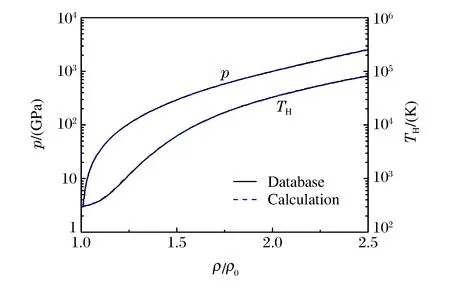
圖1 鎢合金W89Mo9Fe1Ni1的沖擊雨貢紐曲線Fig.1 Hugoniot curve of tungsten alloy W89Mo9Fe1Ni1
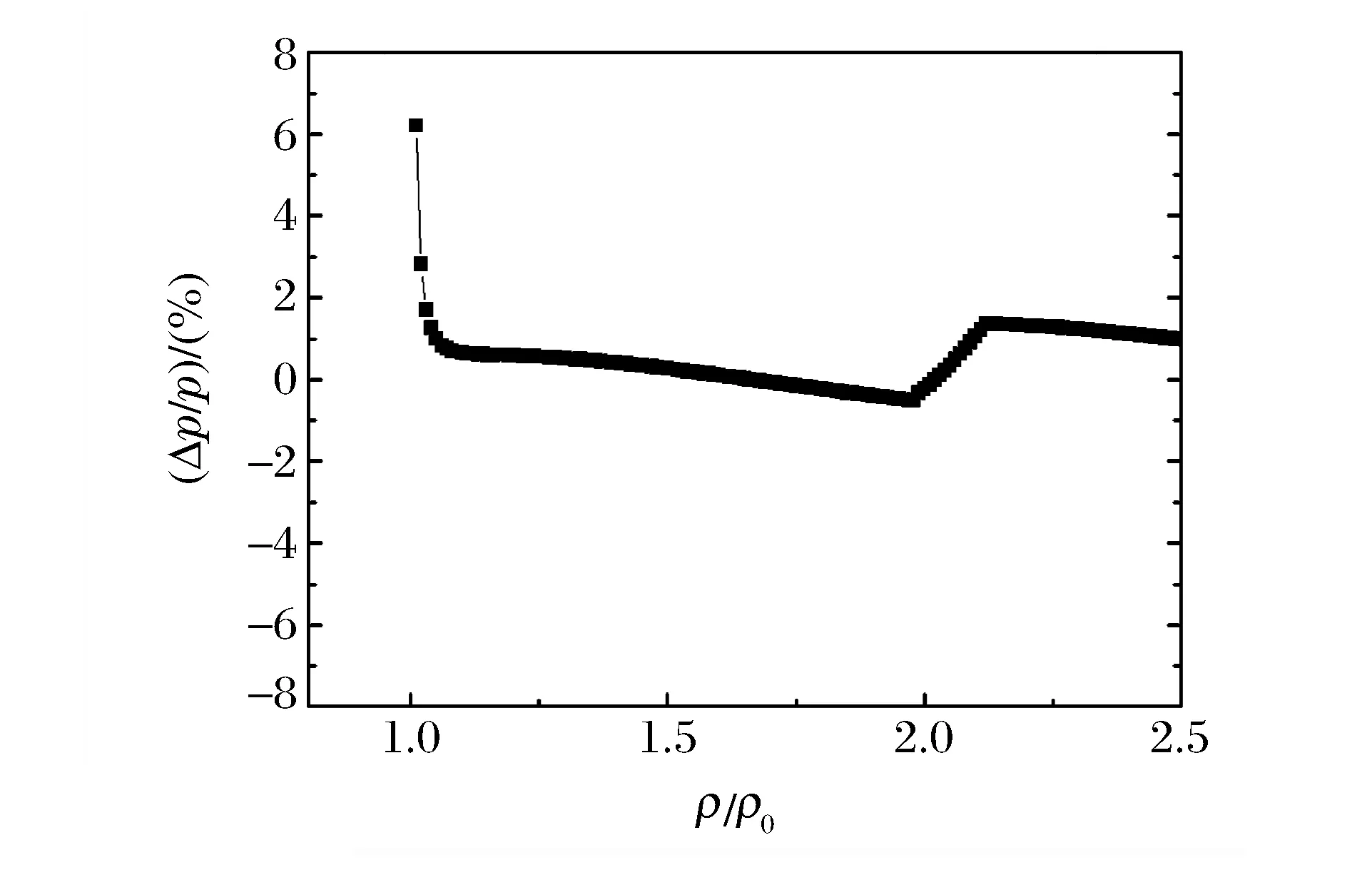
圖2 兩種狀態方程得到的鎢合金沖擊壓強的相對差異Fig.2 Relative difference of shock pressure obtained from two equations of state
圖3顯示了采用兩種狀態方程計算得到的壓強和內能的相對差異(分別為Δp/p和ΔE/E)隨密度變化的曲線。可以看到:對于壓強,兩者之間的相對差異小于2.5%;對于內能,相對差異小于1.5%。作為對照,圖4顯示了由混合物狀態方程計算的鎢合金壓強和內能與純鎢之間的相對差異。可以看到,壓強的相對差異大于11%,內能的相對差異大于4%。表明雖然合金的主要成分是鎢,但其熱力學性質與純鎢有一定的差別,本研究給出的理論模型可以區分這一差別。
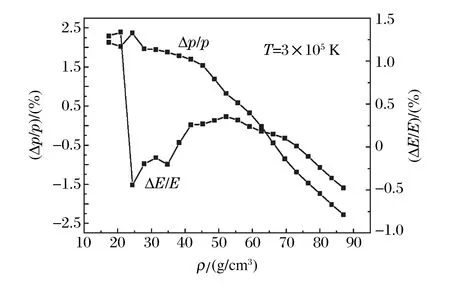
圖3 兩種狀態方程得到的鎢合金壓強和內能的相對差異Fig.3 Relative differences of pressure and internal energy obtained from two equations of state
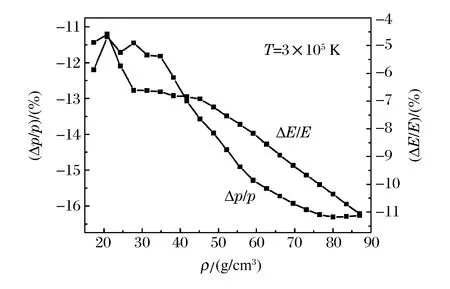
圖4 鎢合金和純鎢的壓強和內能的相對差異Fig.4 Relative difference of pressure and internal energy obtained from tungsten alloy and pure tungsten
4 結 論
基于等溫等壓假設和體積相加原理,給出了由單質狀態方程計算多種組元構成的混合物狀態方程的理論方案,由此可以計算混合物的壓強和內能,同時還可以得到定容比熱容、壓強系數、等溫聲速、等熵聲速等熱力學量。采用該混合物狀態方程,計算得到了一種4組元鎢合金的狀態方程,所得結果與狀態方程庫直接給出的合金狀態方程符合得很好,驗證了物理方案及程序的正確性。
本方案可應用于在高溫高壓狀態下能較好滿足體積相加原理的多組元化合物、混合物及合金的狀態方程計算。
[1] 徐錫申,張萬箱.實用物態方程理論導引 [M].北京:科學出版社,1986:234.
XU X S,ZHANG W X.Introduction to theory of applied equations of state [M].Beijing:Science Press,1986:234.
[2] 王正言,李茂生,陳棟泉,等.混合物物態方程的體積相加模型和熱力學自洽條件 [J].高壓物理學報,1999,13(1):37-41.
WANG Z Y,LI M S,CHEN D Q,et al.Volume adding model and thermodynamic self-consistency for equation of state of mixtures [J].Chinese Journal of High Pressure Physics,1999,13(1):37-41.
[3] 唐 鴿,江少恩,易有根,等.混合物質高壓狀態方程的計算 [J].強激光與粒子束,2008,20(2):247-249.
TANG G,JIANG S E,YI Y G,et al.Calculation of equation of state of a material mixture under high pressure [J].High Power Laser and Particle Beams,2008,20(2):247-249.
[4] 王學容,王建國.混合物物態方程的計算 [J].強激光與粒子束,2011,23(8):2083-2089.
WANG X R,WANG J G.Calculation of equation of state of material mixture [J].High Power Laser and Particle Beams,2011,23(8):2083-2089.
[5] CRANFILL C W.EOS of a material mixture in pressure equilibrium:LA-13661 [R].Los Alamos:Los Alamos National Laboratory,2000.

