一種部分響應CPM信號的調制參數盲估計算法

靳曉艷，李　偉

(1.中國電子科技集團公司第五十四研究所，河北 石家莊 050081；

2.空軍駐石家莊地區軍代室，河北 石家莊 050081)

?

一種部分響應CPM信號的調制參數盲估計算法

靳曉艷1，李偉2

(1.中國電子科技集團公司第五十四研究所，河北 石家莊 050081；

2.空軍駐石家莊地區軍代室，河北 石家莊 050081)

摘要針對非協作通信環境下部分響應CPM信號的調制參數盲估計問題，提出了一種系統的參數估計方案，可依次對載波頻率、符號速率、調制指數和調制階數進行有效地估計。在基于循環平穩特性的符號速率估計的前提下，對聯合估計算法進行簡化，構造新的代價函數，實現載波頻率和調制指數聯合估計，提取循環譜線特征估計調制階數。仿真試驗表明，該算法在信噪比10 dB時具有較好的估計效果。

關鍵詞CPM；調制參數；盲識別；循環譜

A Blind Modulation Parameter Estimation Algorithm for Partial Responses CPM Signal

JIN Xiao-yan1,LI Wei2

(1.The54thResearchInstituteofCETC,ShijiazhuangHebei050081,China；2.MilitaryRepresentativeOfficeofPLAAirForceStationedinShijiazhuangRegion，ShijiazhuangHebei050081,China)

AbstractA systematic scheme is proposed to solve the problem of modulation parameter estimation for partial responses CPM signal in non-cooperative communication environment.It can successively estimate carrier frequency,symbol rate,and modulation index and modulation order.After the estimation of symbol rate based on the features of cyclostationary of CPM signals,the joint estimation algorithm is simplified and a new cost function is constructed to estimate frequency offset and modulation index jointly.Lastly the modulation order is estimated by picking up features of cyclic spectrum line.Simulation results indicate that the algorithm can provide great performance under the SNR of 10 dB.

Key wordsCPM;modulation parameter;blind recognition;cyclic spectrum

0引言

連續相位調制(CPM)是一種相位連續、包絡恒定的調制方式[1]，具有很高的頻譜利用率和功率利用率，在現代移動通信和衛星通信系統中獲得了廣泛的應用，目前許多戰術跳頻電臺也采用了這種調制樣式[2]。因此，近幾年通信偵察中頗為重視針對這種調制方式的信號盲檢測和參數的分析識別技術。

在CPM調制參數盲估計方面，文獻[3-7]中使用一些傳統的基于信號循環平穩特性的方法可以實現全響應CPM信號參數盲估計，但對于部分響應CPM信號，過寬的信號過渡帶寬會導致這些算法失效。文獻[8-9]中使用高階累積量對調制指數進行盲估計，但該算法也同樣只適用于全響應CPM信號。本文提出了一種CPM信號的調制參數盲估計方法，能夠適用于包括部分響應信號在內的全部類型CPM信號，并通過仿真試驗驗證了算法的有效性。

1CPM信號的數學模型

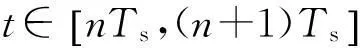
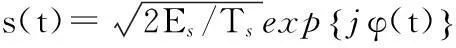
(1)

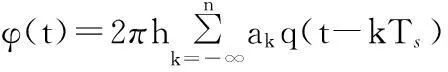
(2)

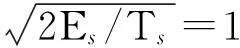
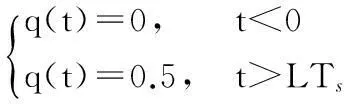
(3)

q(t)可以表示為頻率成形脈沖g(t)的積分，

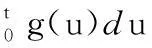
(4)

g(t)僅在區間(0,LTs]內具有非零值，LTs為頻率成形脈沖的持續時間，正整數L稱為頻率成形脈沖相關長度，當L=1時，稱為全響應CPM信號；當L>1時，稱為部分響應CPM信號。

2CPM信號的參數估計

對CPM信號進行參數估計時，需要估計的參數有：載頻fc、符號速率Rs、調制指數h和調制階數M。文獻[10]提出的調制指數/頻偏/符號速率聯合估計算法，需要的參數先驗信息較少，并且具有很好的估計效果。然而該算法中符號周期搜索區間的確定非常困難，尤其對于部分響應CPM信號，帶寬受成形波形長度的影響，于是用粗略估計的帶寬來確定符號周期搜索區間往往導致聯合估計錯誤。本文對該聯合算法進行了改進，即先采用循環譜算法對符號速率進行精確估計，再利用簡化后的聯合算法進行調制指數和頻偏的聯合估計。因此，CPM信號參數估計方案如圖1所示。

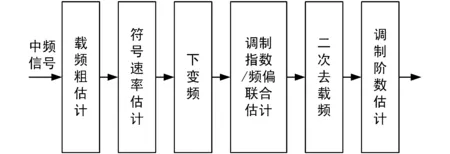
圖1　CPM信號參數估計流程

2.1載頻粗估計

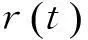
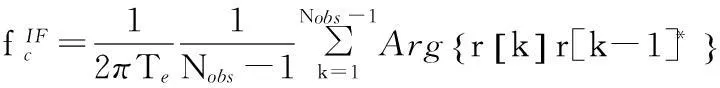
(5)

2.2符號速率估計

CPM信號在譜頻率為載頻的循環截面上，有等間距的離散譜線，且其間距為信號的符號速率[11]。因此可以利用信號循環譜截面特征，直接對接收的中頻信號進行符號速率估計。

因此，對接收到的CPM信號，用頻域譜平滑法得到其循環譜估計，利用非線性濾波方法提取譜頻率為載頻的循環截面上的離散譜線，根據該截面上離散譜線的分布距離，得到符號速率的估計。

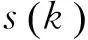
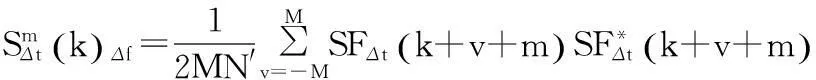
(6)

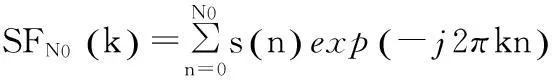
(7)

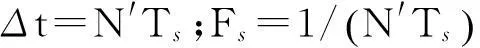
2.3調制指數和頻偏聯合估計

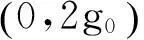
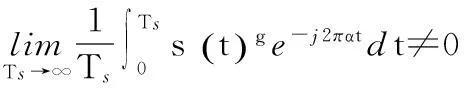
(8)

由于本參數估計方案中已經對符號速率進行了精確估計，因此可對文獻[10]算法進行簡化，定義代價函數為：

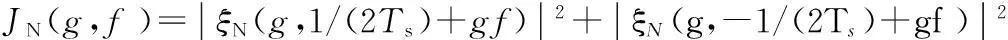
(9)

2.4調制階數估計

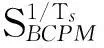
(10)

因此，四進制CPM信號的循環譜在f=0和f=±1/Ts處出現3根離散譜線。同理，八進制CPM信號的循環譜存在7根離散譜線。可見，對于調制指數h=1時不同調制階數的CPM信號，在循環頻率α=1/Ts處的循環譜具有不同的離散譜線特征，因此可以根據α=1/Ts處循環譜的譜線結構來對CPM信號的調制階數進行識別。

對于h≠1的CPM信號，需要對h進行調整，使得調整后的調制指數h′滿足h′=1。令μ=1/h，對CPM信號進行μ次方運算：

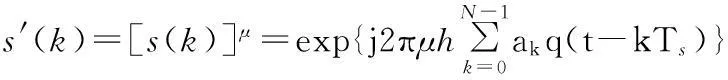
(11)

s′(k)即為調整后的CPM信號，對s(k)的μ次方運算僅僅改變其調制指數，對其他的調制參數沒有影響，因此調整后的CPM信號也具有以上分析的循環平穩性。

3算法仿真與性能分析

通過仿真試驗驗證本文所提算法的有效性。假設四進制CPM信號的符號速率Rs=200 ksps；載波頻率fc=400 kHz；采樣率fs=2 MHz；觀測碼元長度N=1 024；成形脈沖為升余弦脈沖，成形波形長度L=2；調制指數h=2/5。

下面給出了使用本文算法對上述信號進行參數估計的結果。f=fc的循環譜截面如圖2所示，根據離散譜線位置可正確估計符號速率；調制指數和頻偏聯合估計的代價函數分布圖如圖3所示，根據最高點位置可正確估計調制指數與頻偏；α=1/Ts的循環譜截面如圖4所示，根據譜線根數與位置可正確估計調制階數。此外，該算法對于全響應CPM信號同樣適用。

圖2　f=fc的循環譜截面

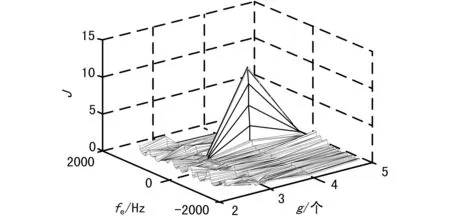
圖3　代價函數分布

隨信噪比的變化，使用本文算法對上述仿真條件下的CPM信號進行100次蒙特卡羅試驗的統計結果如表1所示。可以看出，當信噪比達到10 dB以上時，本算法能夠有效估計符號速率、載頻、調制指數和調制階數。

表1　不同信噪比下CPM信號參數估計結果

4結束語

在非協作數字通信系統中要實現CPM信號的盲解調，接收端首先需要完成信號調制參數的盲估計。本文研究了部分響應CPM信號調制參數盲估計問題，提出了一種系統的參數估計方案，可以有效地對部分響應CPM信號的載波頻率、符號速率、調制指數以及調制階數進行估計，并通過仿真試驗對本文所提算法進行了性能驗證。

參考文獻

[1]周家喜.非協作通信中連續相位調制信號盲解調關鍵技術研究[D]．合肥：中國科學技術大學，2009.

[2]周家喜，徐佩霞，戴旭初．一種基于循環平穩性的CPM信號調制階數盲識別算法[J].信號處理，2010，26(4):578-580.

[3]楊書玲.一種CPM信號參數盲估計方法[J].無線電通信技術，2013，39(2):29-35.

[4]CIBLAT P,LOUBATON P,SERPEDIN E.et al.Asymptotic Analysis of Blind Cyclic Correlation Based Symbol Lrate Estimation[J].IEEE Transactions on Information Theory，2002，7(7):1 922-1 934.

[5]GARDNER W A.Statistical Spectral Analysis:A Nonprobabilistic Theory[M].Englewood Cliffs，NJ:Prentice-Hall，1988.

[6]吳厚明，吳量，江樺．一種基于循環平穩性的CPM信號符號速率盲估計算法[J]．信息工程學院學報，2012，13(2):224 -228.

[7]王寧，彭華，崔偉亮．一種非輔助數據的連續相位調制信號符號速率估計算法[J]．信號處理，2010，26(12):1 864-1 869.

[8]FONOLLOSA J R,FONOLLOSA J A R.Estimation of the Modulation Index of CPM Signals Using Higher Order Statistics[J].ICASSP,Minneapolis,1993(4):268-271.

[9]NIKIAS C L,FONOLLOSA J R.Analysis of CPM Signals Using Higher Order Statistics[J].MILCOM,1993(2):663-667.

[10]BIANCHI P,LOUBATON P,SIRVEN F.Nondata Aided Estimation of the Modulation Index of Continuous Phase Modulation[J].IEEE Transactions onSignal Processing.2004,52(10):2 847-2 861.

[11]NAPOLITANO A,SPOONER C.Cyclic Spectral Analysis of Continuous-phase Modulated Signal[J].IEEE Transactions on Signal Processing，2001,49(1):30-44.

[12]ZHANG Zi-bing,LI Li-ping,XIAO Xian-ci.The Characteristic Analysis of Second Order Cyclostationarity of Continuous Phase Modulation Signal[J].Journal of Electronics & Information Technology,2005,27(11):1 726-1 731.

[13]NAPOLITANO A,SPOONER C M.Cyclic Spectral Analysis of Continuous-Phase Modulated Signal[J].IEEE Trans.on SP,2001,49(1):30-44.

靳曉艷女,(1984—)，博士，工程師。主要研究方向：電子對抗。

李偉男,(1983—)，工程師。主要研究方向：信號與信息處理。

作者簡介

中圖分類號TN 911.7

文獻標志碼A

文章編號1003-3106(2016)04-0026-04

基金項目：國家部委基金資助項目。

收稿日期：2016-01-06

doi:10.3969/j.issn.1003-3106.2016.04.07

引用格式：靳曉艷，李偉.一種部分響應CPM信號的調制參數盲估計算法[J].無線電工程,2016,46(4):26-29.