線性規劃在財務管理中的應用

姚 遠

線性規劃在財務管理中的應用

姚 遠

線性規劃是一種被用于解決實際問題的科學方法。本文先是簡單介紹了線性規劃的含義及數學模型，接著重點闡述了其在財務管理中的兩大應用，通過案例說明的方法，推導線性規劃如何解決成本管理層面求花費最少的問題和投資決策層面求回報最大的問題。最后，本文肯定了財務管理中線性規劃的重大意義，并提出了一點注意。

線性規劃；數學模型；成本管理；投資決策

一、線性規劃的概念及數學模型

線性規劃是運籌學中一個較為成熟而又應用廣泛的重要分支，主要研究線性約束條件下線性目標函數的極值問題，線性規劃也是一門幫助人們進行科學管理的數學理論和方法。目前，線性規劃的求解法有圖解法、單純形法等。其中，利用單純形法在計算機求解最為常見。線性規劃的數學模型由三大部分構成：決策變量、目標函數和約束條件。決策變量是人們針對實際問題需要考慮和控制的因素，也是需要求解的未知變量；目標函數是與決策變量存在線性關系的最值方程；而約束條件則是人們實現最優目標所必須滿足的限制性因素。所以，從實際問題出發，構建線性規劃的數學模型需要依次確定影響目標實現的決策變量，確定決策變量和最優目標之間的函數關系，以及確定決策變量必須遵從的約束條件。

二、財務管理中線性規劃的應用

線性規劃旨在解決目標是什么、約束條件下我們能做什么的問題。而財務管理則是在整體目標驅動下，進行資產購置、資本融通和經營管理的經濟活動。所以，用線性規劃去解讀財務管理，即是如何在限制條件下合理調度資源、實現企業目標。事實上，線性規劃已經證明了可以解決包括人力資源分配、生產計劃安排、套裁下料在內的很多問題。但是，線性規劃在財務管理中的應用還是以成本管理問題和投資決策問題最為典型。

（一）成本管理方面

現代財務管理和會計學同屬工商管理門類下，而區別這兩者的一大顯著特征即是是否重視管理職能。因為，基于理性的經濟人假設，當面對資源稀缺以及利益驅動，經濟個體就會自主進行資源分配。而資源分配就是最原始形態下的財務管理。于是，現代財務管理在這一主旨下不斷拓展，進一步研究有效利用人、財、物的方法。因而，成本管理應運而生，并且逐漸成為現代財務管理的重大分支。企業重視成本管理，是因為當今社會經濟環境競爭激烈，對手之間的價格戰役層出不窮，所以每節約一分的成本，就意味著同等銷售價格下的更高利潤，也確保了公司得以存續的核心競爭力。而企業的成本管理問題其實就是如何保證在實現同等的效用目標前提下，能夠耗費最少的成本。所以，這與線性規劃模型最優化法的理念是相對應，本文認為可以采用線性規劃模型來解決企業成本管理問題。

實際上，生產制造類企業所涉及的成本管理問題尤為典型，包括原材料的消耗、生產流程的優化等。本文將針對農產品生產企業的施肥成本管理問題，特別是基于不同復合化肥的選用問題，采用線性規劃分析法，將實際問題轉化為數學模型，對成本方案進行量化評估，以選擇最優解。

例：康健公司是一家以種植天然農作物并生產綠色農產品而聞名的企業，公司重點種植的綠葉芥藍一直暢銷全國。近年來，公司的生產和銷售成本等均大幅增長。所以，為了保證盈利，公司決定嚴格控制各項成本耗費。已知，單位綠葉芥藍的生產過程中，至少需要氮、磷、鉀分別為48kg、36kg和63kg。而目前可選用的復合化肥有A、B、C、D四種。并且各復合化肥每公斤所含元素的數量以及每公斤的價格均參見下面的列表。現在，康健公司需要通過成本管理，選擇花費最少的施肥方案。

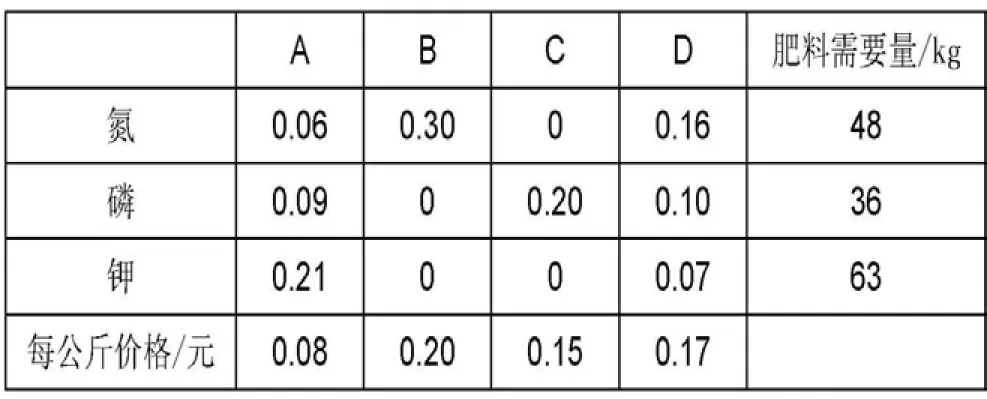
解：設X1、X2、X3、X4分別表示A、B、C、D四種復合化肥的公斤數，C表示康健公司所需花費的總成本，則這一成本管理問題轉化的數學模型為：

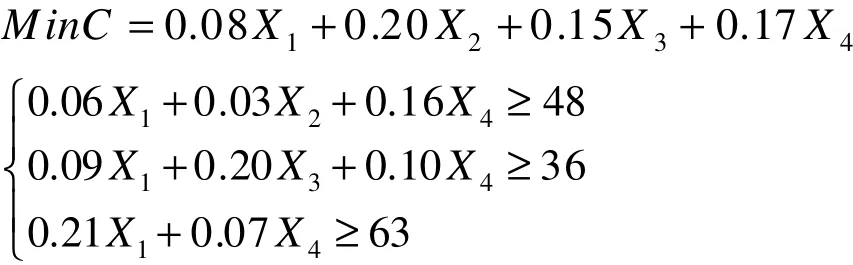
借助工具The Management Scientist Version 6.0進行運算求解。由此得康健公司的最優成本管理方案為：購買復合化肥A 400公斤，購買復合化肥B 80公斤。所以康健公司種植單位綠色芥藍所需花費的最少成本為Min C= 48（元）。

（二）投資決策方面

全球經濟一體化格局的形成使得企業的成功面臨著更多競爭與挑戰，于是，投資活動作為企業重要的“造血”活動，理應為企業提供豐富的收益回報，以確保其高質量的可持續發展。但是，即便是基于最理想化的經濟環境，假設所有的投資均能產生效益，投資方案的實施也避免不了受到諸多條件的限制，比如企業投資項目可動用資金的有限性和社會對不同投資項目可預期的收益率等。而這些客觀條件又是企業在做投資決策時所必須遵守且不可違背的。此外，企業進行投資活動，除了滿足社會需求，歸根結底還是為了自身的獲利。因而，如何做到利潤最大化一直以來都是企業秉持的終極投資目標。所以以一言蔽之，企業的投資決策即是在總資金一定、各項目收益確定的限定條件下，努力去尋求可實現投資組合回報最大化的經濟活動。而這也正好符合線性規劃模型最優化法的理念。所以，本文認為采用線性規劃模型解決投資決策問題就顯得頗為適用了。

在現實中，企業所經歷的投資決策問題有許多，例如工程項目的投資選擇、證券類組合的投資選擇等。本文將針對工程項目的投資決策問題，特別是基于不同產品生產線的購買問題，采用線性規劃分析法，將實際問題轉化為數學模型，對投資方案進行量化評估，以選擇最優解。

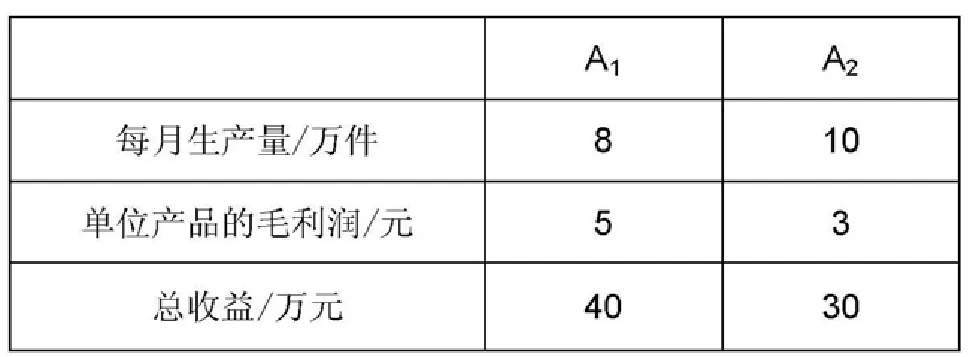
例：東方公司是一家老牌制造業企業，一直以來致力于生產各種生活用品。近日，東方公司根據市場調研決定投資購買有關運動水杯的生產線。已知構建生產線所必須的原材料有B1、B2和B3。而目前，公司可動用資金只夠采購三種原材料的供應量分別300噸、500噸和600噸。此外，公司發現較為暢銷的運動水杯有A1和A2兩種，單位產品的毛利潤分別為5元和3元。其他相關數據參見下面的列表。現在，東方公司需要選擇能獲得最大利潤的生產線投資方案。

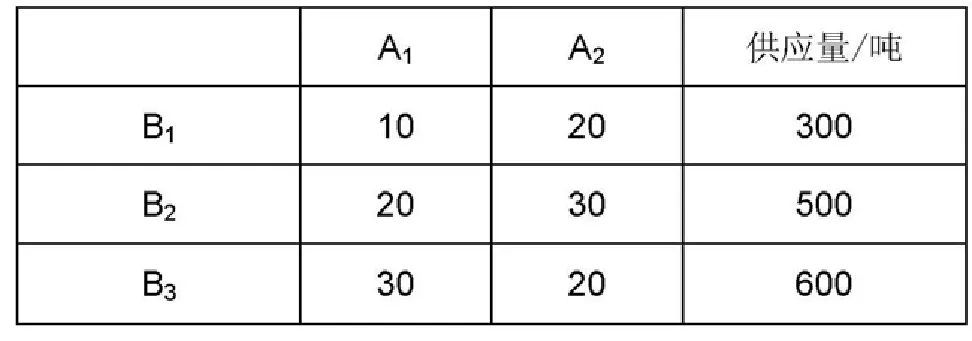
解：設X1、X2分別表示運動水杯A1、A2生產線的個數，W表示東方公司可獲得的總利潤，則這一投資決策問題轉化的數學模型為：

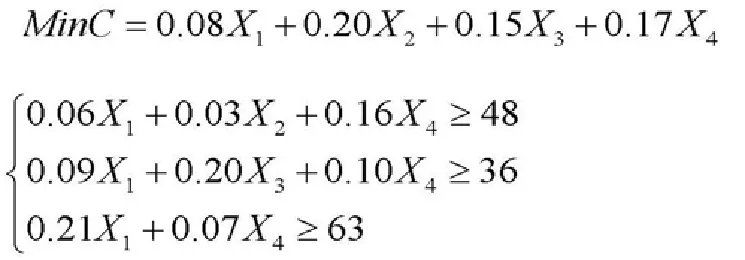
借助工具The Management Scientist Version 6.0進行運算求解。

由此得東方公司的最優投資方案為：構建運動水杯A1的生產線16個，構建運動水杯A2的生產線6個。所以東方公司每月可獲得的最大利潤為Max W = 820（萬元）。

綜上可見，在確定了決策因素、目標函數和約束條件后，實際問題即演變成為數學模型。于是，線性規劃就能很好地解決企業財務管理中的相關選擇問題了。

三、結語

線性規劃從大量數據出發，嚴格遵從理論基礎，確保演算結果的科學性和可靠性。同時，線性規劃又從企業實情出發，全面兼顧種種限制，保證最優方案的適用性和可行性。所以，線性規劃對企業財務管理有著重要的意義，具有很好的應用前景。并且，隨著計算機技術的日趨臻善，線性規劃的運用必將愈發簡便易行。也可以預期，線性規劃在財務管理領域的應用會不斷深化，以持續提高企業的經營效率。但是，有一點需要注意的是，線性規劃模型表現為靜態性，即在構建企業財務管理活動時所涉及的價格、回收期等因素，假設其系數為常數。所以，由此推導出的最優解實際上是近似值，企業還需要結合問題的誤差綜合去考慮。

[1]黃玲花.線性規劃在現代管理中的應用[J].廣西商業高等專科學校學報,2004,12:75-77.

[2]李麗麗.線性規劃模型在農村經濟中的應用[J].洛陽師范學院學報,2015,05:117-119.

[3]劉春艷.線性規劃在經濟管理中的應用[J].電力學報, 2008,06:37-42.

[4]束金龍,聞人凱.線性規劃理論與模型應用[M].北京:科學出版社,2010:1-10.

[5]孫艷華.工商管理中線性規劃的應用探析[J].經營管理者,2013,09:202.

中南財經政法大學會計學院）