均勻電場中的橢球形導體

趙 強 曲 哲（西安交通大學理學院，陜西西安 710049）

?

均勻電場中的橢球形導體

趙 強 曲 哲
（西安交通大學理學院，陜西西安 710049）

摘 要本文利用“一個均勻極化的電介質(zhì)橢球，其表面的極化電荷在橢球內(nèi)產(chǎn)生一個與極化方向嚴格相反的均勻電場”這個觀點，以均勻極化的旋轉橢球形電介質(zhì)為模型，用類比的方法導出了均勻外電場中旋轉橢球形導體表面電荷的分布規(guī)律．

關鍵詞旋轉橢球；導體；均勻極化；靜電場的唯一性

鐘錫華先生偏愛余弦型球面電荷的觀點給筆者印象深刻［1］，他的這個愛好必然會給學生帶來這樣一個疑問：既然將球形導體放到均勻外電場E0中，導體的表面上將會出現(xiàn)余弦型電荷分布，那么，如果將一個旋轉橢球形導體放到均勻的外電場E0中，其表面的感應電荷將如何分布？還是余弦型分布嗎？

一般來說要回答這個問題，需求解靜電場的拉普拉斯方程．然而學生只有學了電動力學這門課程后，才有求解拉普拉斯方程的能力，然而即使學生有了這個能力，求解拉普拉斯方程也并非易事，因此，這個疑問將在相當長一段時間內(nèi)困擾學生．但是如果我們利用E．M．珀塞爾的“只有橢球型的電介質(zhì)（圓球是它的一個特例）才能在均勻電場中均勻極化．”的觀點［2］，通過計算均勻極化的旋轉橢球形電介質(zhì)表面極化電荷的分布規(guī)律，就可用類比的方法給出均勻外電場中旋轉橢球形導體表面的感應電荷的分布規(guī)律．這樣不僅避開了求解拉普拉斯方程，用普通物理的方法回答了學生的疑問，而且物理圖像清晰，富有啟發(fā)性．下面我們分3種情況來討論這個問題．

1 外電場E0的方向沿旋轉橢球形導體的旋轉軸

我們暫時拋開導體問題不說，先考慮一沿旋轉軸均勻極化的旋轉橢球形電介質(zhì)．設此介質(zhì)橢球的旋轉軸為z軸，介質(zhì)極化強度P指向z軸的正方向，則此旋轉橢球上的直角坐標方程為

此橢球的參數(shù)方程為

根據(jù)微分幾何的知識［3］，旋轉橢球在用式（2）表示的情況下，其表面上任一點A（x，y，z）處的法向n和z軸夾角α（同時也是法向n和P之間的夾角）的余弦為

在A點處極化電荷的面密度為

同樣根據(jù)微分幾何的知識，若橢圓用參數(shù)方程（2）表示，其表面的面積微元為

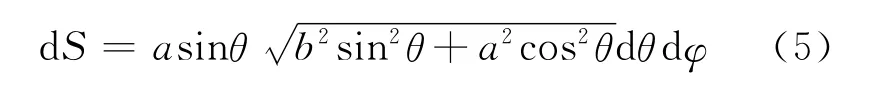
面元dS上的電量為

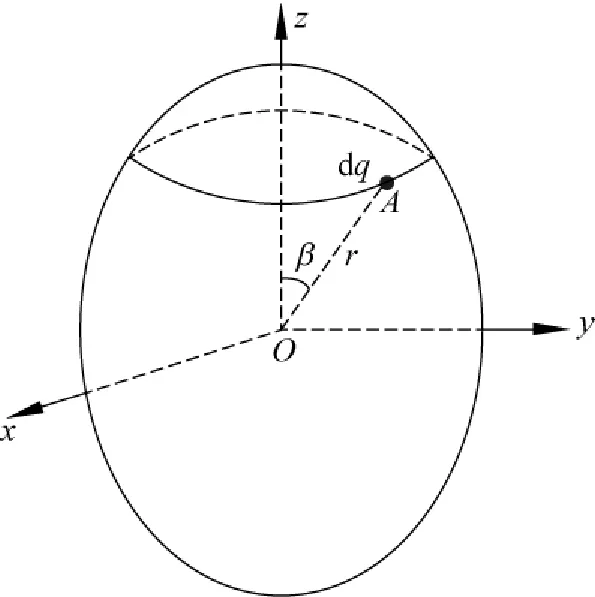
圖1　橢球形電介質(zhì)

根據(jù)E．M．珀塞爾的觀點，均勻極化的橢球形電介質(zhì)內(nèi)的退極化場為均勻．因此我們只要計算出其表面極化電荷在其中心O點的場，其內(nèi)部所有點的電場就清楚了．電荷dq在橢球中心O處電場在z軸上的分量為

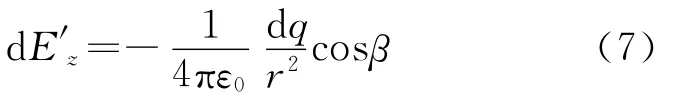
如圖1所示，式（6）中的r為dq到橢球中心的距離，其用參數(shù)θ，φ表示的形式為

β為r與z軸之間的夾角（注：β和參數(shù)θ并非一回事），其余弦為

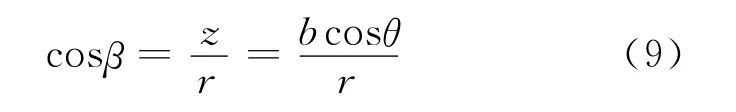
將式（8）和式（9）代入式（7）有橢球中心O點的電場為

幸運的是積分表中可以查到式（12）的積分，查積分表，并定義定義介質(zhì)橢球的退極化因子為（k可稱為橢球的形狀因子），計算并整理后有

若a＜b，即k＞1（“雞蛋”形旋轉橢球）

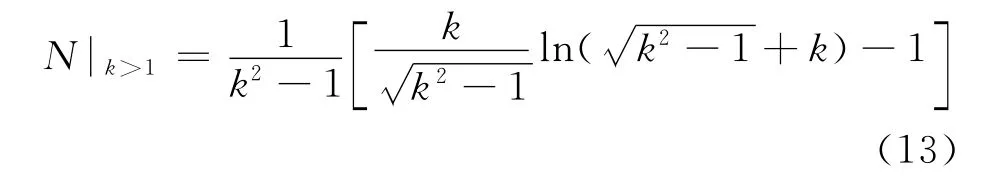
若a＞b，即k＜1（“鐵餅”形旋轉橢球）

將式（14）和式（4）綜合起來考慮，得到均勻極化的旋轉橢球形電介質(zhì)表面極化電荷面密度和極化電荷產(chǎn)生的退極化電場E′（E′＝｜E′z｜）之間的關系為

將式（13）或式（13′）代入（11）式有

現(xiàn)在我們回到導體問題上．若將一旋轉橢球形導體放到均勻的外電場E0中，E0沿導體的旋轉軸方向，那么根據(jù)導體的靜電平衡條件，橢球表面的感應電荷將在導體內(nèi)產(chǎn)生與E0大小相等方向相反的場將E0抵消掉．根據(jù)靜電場的唯一性定理，這旋轉橢球形導體上的電荷分布規(guī)律應與式（15）一樣，即

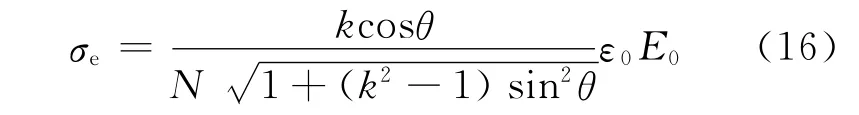
當a＝b，即k＝1時，此導體橢球退化成導體球，參數(shù)θ也退化成r和z軸之間的夾角這時式（15）變?yōu)槭剑?6′）正是鐘錫華先生偏愛的余弦型球面電荷．

2 均勻外電場E0與旋轉橢球形導體的旋轉軸垂直

若外電場E0與導體的旋轉軸z軸垂直．不妨設E0沿y軸方向，這時我們可選沿y軸方向均勻極化的同形狀電介質(zhì)橢球作為模型進行研究．與情況1中不同的是電介質(zhì)橢球表面上任一點A處的法線向n與P之間的夾角α′（亦即n與y軸之間的夾角）的余弦為

電介質(zhì)橢球表面極化電荷的分布為

與情況1類似，我們?nèi)栽跈E球表面上選一小面元dS，dS上的電荷dq的參數(shù)表達式仍與式（6）相同，dq在橢球中心的電場在y軸上的分量為

如圖2所示，與情況1中相同的是β′是r與y

圖 2

軸的夾角，且

做與情況1中類似的運算，極化電荷在O點的電場為

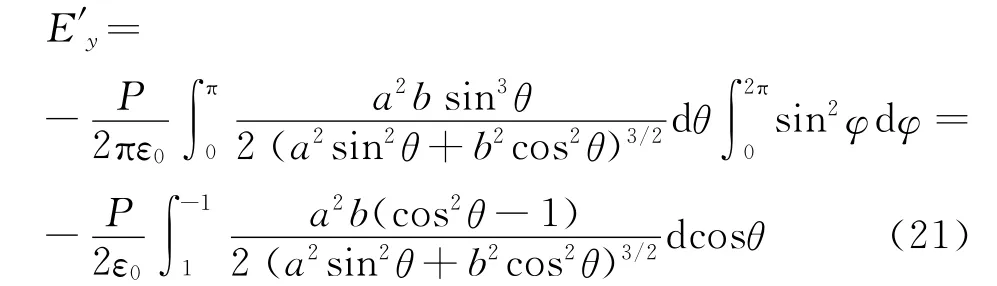
利用式（12），可將式（21）寫成

查積分表，計算并整理后有

將式（23）代入式（22）有

利用式（18）和式（24），我們可以得到均勻極化旋轉橢球形電介質(zhì)其表面極化電荷面密度和退極化場E′（E′＝｜Ey｜）之間的關系

與情況1的道理相同，情況2中的導體橢球表面感應電荷的分布規(guī)律為

3 均勻外電場E0與旋轉橢球形導體的旋轉軸成任意角度

若外電場E0與旋轉橢球形導體的旋轉軸成任意角度α0，我們可以將外電場E0分解為沿旋轉軸z軸的分量E0cosα0和沿y軸的分量E0sinα0（由于旋轉對稱性，我們將y－z平面選得與E0平行，這完全可代表普遍情況），這兩個分量所引起的感應面電荷分布分別為式（16）和式（26）．根據(jù)靜電場的疊加原理和唯一性定理，這時旋轉橢球形導體的表面感應電荷分布規(guī)律為

至此，困擾學生的疑問得到了徹底解決．

參考文獻

［1］ 鐘錫華．電磁學通論［M］．北京：北京大學出版社，2014：3（序），52－56，98－99，127．

［2］ 珀塞爾E M．電磁學［M］．伯克利物理教程第二卷．南開大學物理系，譯．北京：科學出版社，1979：406．

［3］ 史瑞鰲，眭潔，孫澈．高等數(shù)學講義（下冊）［M］．北京：高等教育出版社，1989：176，226．

ELLIPSOIDAL CONDUCTOR IN UNIFORM ELECTRIC FIELD

Zhao Qiang Qu Zhe
（College of Science，Xi’an Jiaotong University，Xi’an，Shanxi 710049）

AbstractBased on the model of an uniformly polarized dielectric rotation ellipsoid and the viewpoint that the surface polarization charges of an uniformly polarized dielectric ellipsoid can produce the uniform electric field in contrast to the polarization direction strictly，in this paper，we deduced the surface charge distribution of the rotation ellipsoidal conductor in the uniform electric field by the analogy method．

Key wordsrotation ellipsoid；conductor；uniform polarization；the uniqueness of electrostatic field

收稿日期：2015－07－31