初中數學“課題學習”教學策略初探
張敏捷

[摘 要] 課題學習作為一種全新的學習方式,給學生提供了實踐性、探索性和研究性學習的渠道,有利于培養學生主動探究和研究的精神,發展數學能力. 本文從初中數學“課題學習”的類型、基本環節、實施策略三個方面進行了簡要闡述.
[關鍵詞] 初中數學;課題學習
現代數學教學理論指出:學生是學習的主體,教師在課堂教學中要積極倡導學生的學習方式由他主學習變為自主學習,引導自主發現和探索數學研究的過程. 為了給學生提供實踐性、探索性和研究性學習的渠道,人教版初中數學教材新增了“課題學習”這一欄目,其旨在引導學生參與體驗研究性學習過程,培養學生主動探究和研究的精神,發展數學能力. 但在具體教學實踐中,卻存在一些問題和不足. 例如,部分教師只講授一些與中考有關的“課題學習”內容,對于制作立體模型類“課題學習”內容常常忽略,要求學生以自學為主. 顯然,這些問題的存在與新課標的理念存在差距,不利于學生的全面發展.
初中數學“課題學習”的類型
1. 數學建模
數學建模的核心是引導學生從“學數學”向“做數學”轉變,應用數學方法解決現實生活中的實際問題. 對于數學建模類型問題的教學,通常情況下是在教師的引導和啟發下將實際問題數學化,建立數學模型,然后應用所學數學知識進行求解,并進行求證和檢驗. 例如,八年級下冊的“選擇方案”課題學習.
2. 數學調查及分析
數學調查及分析是通過對實際生活中的問題進行調查,尋找問題解決策略的一種學習過程. 其教學的一般過程是調查與實際生活密切聯系的問題,發展學生解決問題的能力,培養學生用數學思維思考問題的習慣和觀念. 例如,七年級上冊的“從數據談節水”課題學習.
3. 數學實驗
數學實驗是借助幾何畫板、多媒體等數學軟件,讓學生在探究問題中形成或檢驗所蘊含的數學知識的一種活動. 對于數學實驗類型的問題,學生能在具體實驗操作中理解和掌握數學知識,從而提高教學效果. 例如,九年級上冊的“圖案設計”課題學習.
當然,以上幾種課題學習的類型并不是孤立的,而是相互滲透、交叉使用的. 同時,“課題學習”的內容是數學基本知識的擴展,是學生對具體知識的應用和升華.
初中數學“課題學習”的基本
環節
1. 準備階段
首先,應明確“課題學習”的主題. “課題學習”的安排都與本章知識的學習緊密相關,都是對相關基礎知識的資料積累和拓展學習. 例如,學習完統計知識后安排“從數據談節水”的學習內容. 其次,明確教學目標,認真分析學情,根據學生的總體學習情況認真備課,設計出科學、合理的教學方案.
2. 實施階段
根據教學目標和所要講授的課題,設置好問題情境,利用影像資料、幾何畫板設計動態課件等引入課題,能最大限度地激起學生探究問題的興趣. 首先,搜集和分析相關的信息資料. 在教師的指導下,學生查閱文獻和書刊雜志,了解一些與課題知識相關的有用信息資料,學會整理和分析資料. 其次,制定出解決問題的措施. 根據資料的整理和分析,總結、歸納出解決問題的具體策略. 對于教學過程中出現的問題,組織學生進行小組交流和討論,共同探討出問題的具體策略. 同時,教師要發揮好自己的指導作用,及時地給予學生提示,幫助學生發現和解決問題. 最后,確定出問題的具體解決方案,在初步形成研究成果的基礎上,鼓勵學生陳述自己的觀點,表達出自己的數學想法,共同探討,確定出問題的具體解決方案.
3. 總結階段
組織學生交流探究問題的心得體會,充分展示出自己的最終研究成果,學會從活動中總結經驗教訓. 同時,教師通過一些鼓勵性評價,繼續保持學生對數學學習的興趣.
初中數學“課題學習”的具體
策略
1. 精心設計,引入課題
(1)通過觀看實物或模型、多媒體動畫演示以及影像資料等,創設出一些現實的直觀問題情境,激起學生的學習興趣和求知欲. 例如,學習“鑲嵌”課題時,通過投影儀展示古代勞動人民在墻面上制作的各種鑲嵌圖案,讓學生直觀感受鑲嵌在生活中的應用.
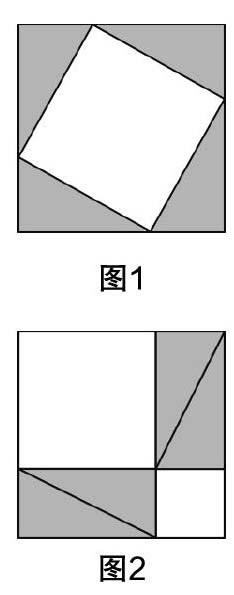
(2)根據課堂的需要,適當地介紹與相關知識背景密切相連的故事、傳說以及歷史人物事跡. 例如,在“拼圖與勾股定理”課題學習中,簡單介紹希臘數學家畢達哥拉斯發現勾股定理的過程,在當時科學十分有限的條件下,通過將圖1中的三角形移動至圖2的位置,證明了圖1、圖2中的白色部分面積相等.
(3)通過讓學生親自參與實驗,提出自己的猜想,在驗證猜想過程中進一步探索和研究課題. 例如,在“設計制作長方體形狀的包裝盒”課題學習時,通過引入“莫比烏斯帶”的數學小實驗,讓學生猜想在不越過紙條邊緣的情況下一只小蟲子能否爬到另一面,并讓學生親自動手實踐.
(4)根據學過的知識,通過創設集知識性和趣味性為一體的實際問題,引入課題學習,充分調動學生解決問題的積極性. 例如,在“選擇方案”課題學習時,王大媽要求賣主退還1斤蘋果的錢是否有道理,引導學生應用一次函數解決實際生活中的問題. 學生可以假設攤主稱重為x斤,實際重量為y斤,通過問題分析,列出函數關系式,即y=x,進一步讓學生感受一次函數在現實生活問題中的應用價值.
2. 合理組織,引導探究
毋庸置疑,學生是學習的主體,教師要在提出問題情境后,將學生置于學習的主體位置上,引導學生勤動腦、動手,讓學生在探索中不斷尋找問題的答案,層層深入進行探究.
例如,在“選擇方案——怎樣租車”課題學習過程中,題目較長且信息量大,不僅有數字,還有表格,如何將題目意思抽象為數學問題呢?教師可以通過“你認為題目要解決的問題是什么”“表格中各數據表示什么含義”等問題來幫助學生理解題意,從而對題目進行抽象概括. 在學生明確題意和需要解決的問題后,教師可先讓學生自行解決,發現不同的學生有不同的租車方式,那么在眾多的租車方案中,哪種方案所需的費用最少呢?引導學生把思考的方向定位在建立函數模型上. 然后,請同學們思考“影響費用的變量是什么”“它和費用之間的函數表達式是什么”“建立哪個變量的函數關系式對選擇方案更加有利”“自變量的取值范圍是什么”……通過這種層層深入的學習和思考,讓學生對數學問題產生親切感. 最后,引導學生總結,通過說說這樣做的理由是什么,應用圖像怎么表示等問題,幫助學生進一步理解函數知識.
3. 合作交流,深化認知
合作交流的學習方式,能夠讓每一個學生都積極地參與到學習過程中,這樣不僅能增進師生之間的相互交流,而且能在有效的合作與討論中讓學生再次經歷知識和技能的學習歷程.
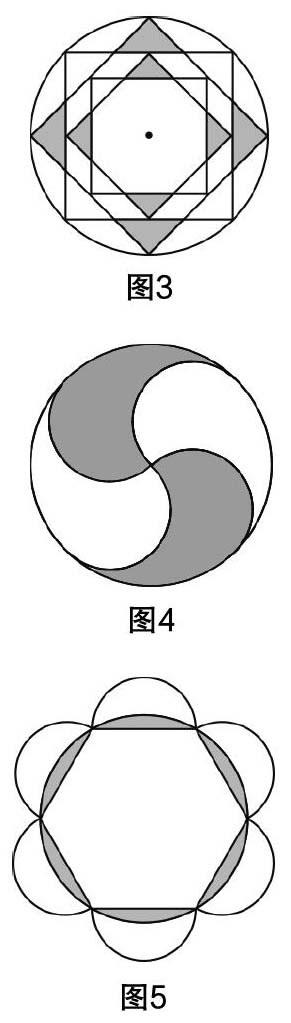
例如,在“圖案設計”課題學習中,要求學生以學習小組的形式觀察圖3、圖4、圖5是由哪些基本幾何圖形組成的,它們的共同點是什么. 可引導學生得出結論:這些組合圖案是由一些基本圖案通過不同的變換得到的. 然后,教師讓每組學生運用三角形、菱形、圓等基本幾何圖形進行圖案設計,在具體圖案設計中熟練掌握平移、軸對稱以及旋轉等知識,最后由各組派代表展示本組的設計成果,其他各代表組則交流、討論圖案的基本圖形,以及圖案是如何形成的.
4. 適時指導,巧妙引領
實時給予學生指導和有效引領是教師應有的責任. 首先,指導學生做好材料的收集、工具器具的準備以及成員分組等課前準備工作,同時,教師要研究清楚課題的背景、制作好多媒體課件,確保教學活動順利進行. 其次,徹底改變教師一言堂的傳統教學形式,鼓勵學生大膽思考,要給予學生獨立思考和合作討論的機會和時間,盡可能地設置學生動手實踐、學生討論、學生展示環節,并認真傾聽和分析每個學生的觀點,提出一些更深入的問題引導學生思考,幫助學生歸納和總結. 最后,認真觀察每個學生的表現,讓每個學生主動地參與活動,分析個別學生參加活動不積極、學習效果不佳的原因,并對每個學生作出科學、合理的評價.
總之,進行“課題學習”具有十分重要的意義,教師要在問題情境、組織以及學習交流方式、實踐指導方面加強研究力度. 只有這樣,才能滿足學生發展的需求,才能與新課標的要求相符合.

