幾何畫板在初中圖形教學中的實例運用

徐凡

[摘 要] 應用幾何畫板可以提高圖形教學的直觀性和準確性，彌補傳統教學方式在直觀感、立體感和動態感等方面的不足，讓學生更深刻地體會到圖形“動”的一面，從而達到改進部分章節教學方法和教學手段的目的，更好地提高課堂效率.

[關鍵詞] 幾何畫板；初中圖形；特色運用

新課改下的初中圖形教學正在發生革命性的變化. 過去的幾何教學一直過分強調演繹推理，卻忽視了“圖形”特征. 新課改的最大亮點，便是恢復“圖形”特征，削弱證明在初中圖形學習中那種“神圣不可動搖”的地位，使初中圖形教學重新煥發生機. 借用學生的話說，圖形“活”了，圖形也可以“動”了. 課程的改革勢必引起教學方法的改革，可不是嗎？現在初中圖形教學的講臺再也不是“粉筆加尺規”了，教學理念的變化加上現代教育技術的普遍應用已經給教學手段，特別是圖形教學帶來了新的變化和改進.

“信息技術與課程的整合”是基礎教育教學改革的新視點，借助多媒體的動畫效果，更有利于向學生展示幾何圖形“動”的一面. 計算機作為一種輔助教學的工具走進課堂教學，可將數學中較為抽象、難理解的概念通過形象具體的事物展現給學生，特別是計算機，可以對數學問題形成動態的演示，彌補傳統教學下教師口述表達的缺乏動態和形象立體感的缺陷. 通過演示處理數學問題，還能激發學生的興趣，增強他們的直觀印象，為教師化解教學難點、突破教學重點、提高課堂效率和教學效果提供一種現代化的教學手段. 幾何畫板正是在這樣的背景下被研發出來的.

現在，我們很欣喜地看到這項工具正在給我們的數學教學帶來更多的革命性變化. 下面就通過初中數學圖形教學的幾個實例，談談幾何畫板對教材中某些知識點進行處理時的獨到之處.

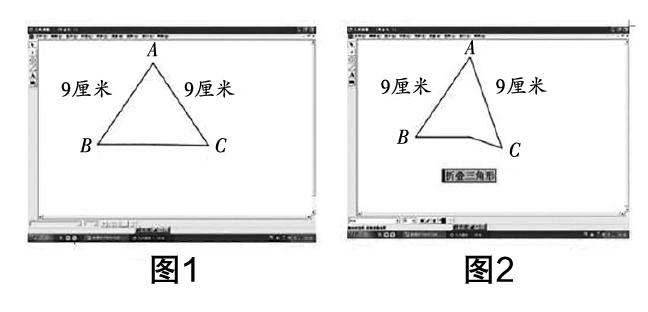
案例1？搖 “等腰三角形”是初中圖形教學的重點內容，這部分有很多定理. 教材在處理方法上引入了較多的動手操作和直觀感知，通過折紙、觀察、歸納等方法能夠較為直觀地得出等腰三角形的有關定義以及性質. 但是，由于學生在動手制作等腰三角形的教學模型時，存在一定的誤差，從而導致結論不是很準確的現象時常發生；而且，學生手工制作的模型帶有一定的局限性，無法很好地解釋等腰三角形中一些結論的一般性與普遍性. 而應用幾何畫板就可以有效避免上述情況的產生. 通過幾何畫板，可以制作折疊、翻轉的動畫效果，這樣的折疊、翻轉很準確，不會出現誤差，得出的結論也就更具有一般性. 此外，運用幾何畫板時，教師還可以通過拖動等腰三角形的頂點來任意改變它的形狀和大小，這樣，能夠更加直觀地給學生展示等腰三角形的變化過程，從而直觀地為學生說明結論的正確性，以及論證結論的一般性. 具體過程如下：

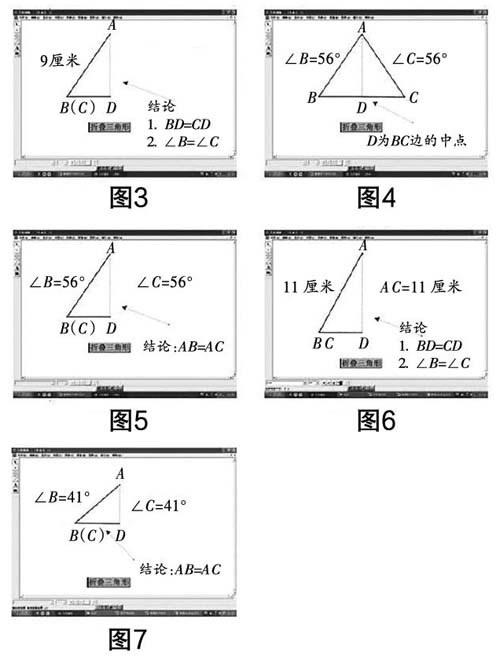
（1）在等腰三角形ABC中，AB=AC（圖1），將AB與AC重合在一起（折疊，圖2），觀察→兩部分會完全重合→等腰三角形是軸對稱圖形，折痕AD是對稱軸，點B與點C重合，BD與CD重合→∠B=∠C，即等邊對等角（圖3）. 通過引導學生對折痕AD進行分析，也就能很容易地得出“三線合一”的性質. 用這種直接的方式得出結論，為后面的推理過程奠定了基礎，而且能讓學生更容易記住結論.

（2）再畫△ABC，使∠B=∠C，D為BC的中點，連接AD（圖4），沿AD對折，觀察→兩部分會完全重合→AB與AC會完全重合，△ABC是等腰三角形，即等角對等邊（圖5）.

（3）拖動等腰三角形ABC的頂點A，改變三角形的形狀，得到不同形狀的符合條件的三角形，然后重復上述步驟（1）和步驟（2），也得到同樣的結論. 讓學生掌握以上結論的一般性（圖6和圖7）.

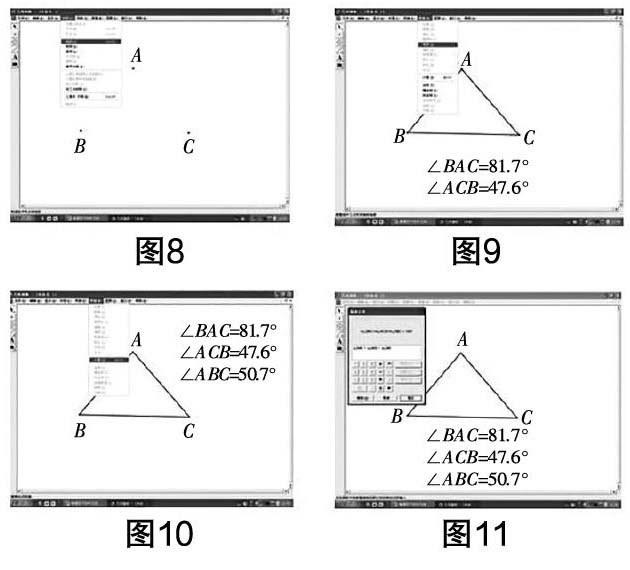
案例2？搖 當我們講解“三角形的內角和定理”時，在以往的教學中，都是教師通過對剪紙的拼接或度量等方式來讓學生感受三角形的內角和等于180°，但這樣的做法在操作時不但誤差很嚴重，而且操作起來也十分麻煩，在很大程度上浪費了課堂教學的時間，所以教學效果一般，沒有預期的那么好. 這時，在幾何畫板的模式下，這個問題就迎刃而解了. 首先，教師可以在幾何畫板中隨意畫出一個三角形（圖8），之后通過電腦操作測量出三角形每個內角的度數，并對其求和（圖9～圖12），之后拖拽三個頂點讓三角形任意變形（圖13的鈍角三角形和圖14的直角三角形），這時同學們會發現，不管三角形的形狀如何變化，所有三角形的三個內角度數的和一直都會是180°，不會改變. 因此，我們可以直接得出三角形的內角和為180°的結論，而不會讓學生懷疑這是個別情況. 這樣的操作，不僅直觀簡便，還省去了教師反復講解演示而效果甚微的教學，也能讓學生在動態模擬下對數學圖形教學產生濃厚的學習興趣，激起他們進行探究的強烈欲望.

案例3？搖 當教師帶領學生一起學習三角形的三條角平分線交于一點、三條高或高的延長線交于一點、三條垂直平分線交于一點、三條中線交于一點時，在以往的教學中，都是教師讓學生用筆自己作圖觀察，并讓學生總結且得出結論，但學生在實際操作過程中會出現相當大的誤差，致使很多同學所作的圖，無法交于一點，還有的學生即使畫線讓其交于一點，也會在心里產生“這會不會只是偶然的個別現象”的疑惑. 這就使得學生很難領會并認可數學內容的本質. 但利用信息技術當中的幾何畫板就可以避免這種現象的發生. 教師可以在幾何畫板中任意畫一個三角形（圖15），之后執行菜單命令，如畫出三條角平分線（圖16）. 由于幾何畫板是計算機操作，準確性非常高，只要命令執行正確就會很容易得到三條角平分線交于一點的事實（圖17），之后再經過教師對三角形的反復變換，仍然能夠讓學生看到這三條線相交于一點的事實并不會隨著三角形的變化而改變（圖18）. 尤其是“高線”這樣特征明顯的線，在拖動過程中還會看到交點的位置變化. （圖19、圖20、圖21）

案例4 幾何畫板對圖形的操作不僅直觀、準確，而且對一些相對抽象的計算推導式定理的學習也有很顯著的效果. 如教學“勾股定理”時，教師可利用“幾何畫板”制作一個不斷發生動態變化的直角三角形，通過滾動的數值計算各邊長度的平方值（圖22讓點A沿AC方向運動），由于幾何畫板中的計算結果是隨著數值變化即時出現的，因此，在教師的引導下，學生通過觀察就會發現所有直角三角形的兩條直角邊的平方之和都會等于斜邊的平方（圖23～圖25），這樣不但省去了讓學生計算得結果的時間，提高教學效率，還加深了學生對勾股定理的印象，有助于學生理解和應用該定理.

學無定法，教同樣也無定法. 幾何畫板的應用讓我們的教學效率明顯得到提高，但是在具體的教學實際應用中也遇到了一些問題，且并不是所有的教學內容都適合用幾何畫板來體現. 因此，教師在教學過程中要注意對教學內容進行篩選，還要注意幾何畫板課件制作的熟練性與美觀實用性，力求能夠為學生呈現出直觀、形象的教學畫面，讓學生產生對初中數學圖形教學的濃厚興趣. 此外，教師之間還要多溝通、多交流，做到教學反思和探索，力爭將幾何畫板的應用效果發揮到最大.