學生在中央的數學課堂

張冬梅 江蘇省特級教師，中學高級教師，南京師范大學教育碩士生導師，南京師范大學、江蘇師范大學“國培計劃”專家委員，南京市瑯琊路小學教師發展中心主任。曾獲全國科研優秀教師、江蘇省先進教育工作者、江蘇省“226”工程培養對象等稱號。多次參加課堂教學評比，獲全國小學數學優化課堂教學評比一等獎、全國優秀錄像課評比一等獎、江蘇省優質課評比一等獎第一名等好成績。

教學風格以“親和”為特色，主張“親和數學親和學”，既關注數學本身的“親和”，又強調要“親和”地學。其領銜的名師工作室致力于“親和數學”的研究，著力構建數學內涵與兒童趣味相和諧的數學學習活動，既關注數學課堂的“數學味”，又關注兒童的生命價值與生活世界，使兒童獲得生命成長。

教學內容：

蘇教版數學五年級下冊《方程》單元第4課時（練習課），練習內容參考第8～13題。

教學目標：

1.通過分享與練習，使學生進一步理解方程的內涵。

2.進一步掌握等式的性質，能根據等式的性質正確地解方程，并形成相應的技能。

3.在自主學習、合作分享的過程中感受數學的魅力，獲得數學學習的方法，提升學生的學習力。

教學準備：

（教師）課件、小黑板；（學生）學習單、錯題集等。

課堂實錄：

一、簡單回顧

師：同學們，這堂課，我們將進行有關“方程”的第一次分享會，回憶一下，我們已經學習了哪些有關方程的知識？

生1：我們學習了什么是等式和什么是方程。（板書：等式和方程）

生2：我們還學習了等式的性質和解方程。（板書：等式的性質和解方程）

二、熱情分享

（一）小組交流

師：關于這兩項內容，大家有些什么學習體會與經驗呢？先請大家在小組內分享，要求（屏幕顯示）：

四人小組任選其中一項內容進行組內交流活動。

（二）全班分享

1.分享有關“等式和方程”的相關知識與學習體會

師：哪些小組是選擇第一項內容的？選兩個代表來跟全班分享。

（一小組的兩位同學上講臺前當小老師跟大家分享，全班互動）

小老師1：我們想先舉個例子考考大家（邊說邊板書）。3+7=10，這是一個等式還是方程？

生3：這只是一個等式。

小老師1：（邊板書邊問）那3+x=10，這又是什么呢？

生4：這也是一個等式，還是一個方程。

小老師1：是的，我們小組認為，等式就是含有等號的式子，而方程是含有未知數的等式。（全班掌聲響起）

小老師2：我們還可以用一幅圖來表示它們的關系。（邊畫邊問）如果我們把世界上所有的等式都放在這個口袋里，那方程應該在哪呢？

生5：方程已經被裝在這個大口袋里面了，應該是里面的小口袋。

小老師2：（邊畫邊講）是的，也就是說，方程一定是等式，等式卻不一定是方程。（熱烈的掌聲再次響起）

2.分享有關“等式的性質和解方程”的相關知識與學習體會

師：同學們用掌聲表達了贊同。那哪個小組愿意來分享第二項內容？

（另一小組的兩位同學上講臺前當小老師跟大家分享，全班互動）

小老師3：（把學習單放在展臺上）

大家看我們這兩題解方程，解第1題的方程時用了等式的哪個性質？

生6：用了等式的第一個性質，就是在等式的兩邊同時加上或減去同一個數，結果仍然是等式。

小老師3：是的，我們在等式的兩邊同時加上6.4，得出方程的解是x=6.8。那第2題用了等式的哪個性質呢？

生7：用了等式的另一個性質，就是在等式的兩邊同時乘或除以同一個不是0的數，結果仍然是等式。

小老師3：是的，我們在等式的兩邊同時乘5，得出方程的解是x=35。

小老師4：我們小組總結了一下，發現不管是用等式的哪個性質來解方程，其實都是為了讓方程的左邊只剩下“x”，就得出方程的解了。（全班掌聲）

師：感謝這個小組分享了用等式的性質來解方程的經驗。那就讓我們利用這些經驗來解方程。

屏幕顯示題目：x÷9=90 x-54=18，學生獨立解方程。

師：來吧，誰愿意跟大家講講是怎么解的？

生8：我在等式的兩邊同時乘9，這樣等式的左邊就剩下x，所以x=810。（掌聲）

生9：為了把方程左邊的“-54”抵消，我在等式的兩邊同時加54，我算得x=72。（掌聲）

師：老師發現英哲同學做得跟大家有些不一樣，英哲，你能跟大家講一講嗎？

生10（英哲）：我是這樣想的，在等式的兩邊同時乘9，那么左邊“÷9”跟“×9”正好可以抵消，所以我就把它們想在心里，直接寫x=90×9。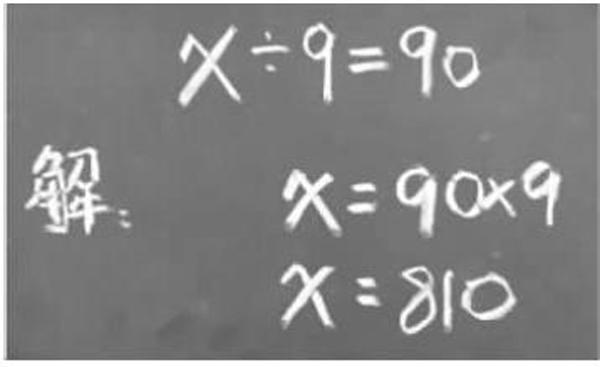

師：誰能上來圈一圈，英哲把什么想在心里了？

生11上來圈：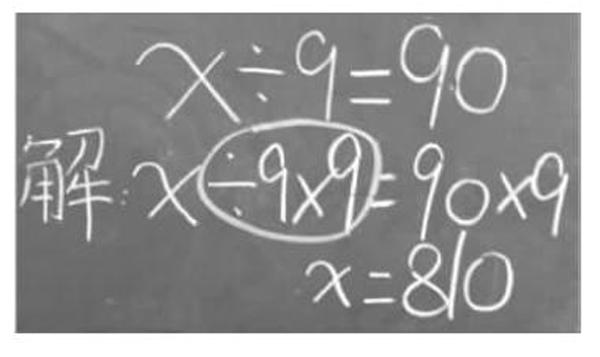

師：那英哲這樣“想在心里”的方法有什么好處嗎？

生12：可以讓解方程來得更簡單，寫起來也更方便。

師：感謝英哲的分享，讓解方程的過程變得更為簡潔。（全班掌聲）那第2題哪些部分我們也可以“想在心里”省略不寫呢？

生13上來圈：

師：以后我們解方程既可以像以前那樣做，也可以用英哲“想在心里”省略寫的方法。我們再練兩題解方程。

屏幕顯示題目：0.9x=2.43 76+x=91，生獨立完成后交流，學生都自覺使用了“想在心里”的方法。

三、質疑解難

師：老師從同學們的眼睛里讀出了智慧與自信。又到了“我是小問號”的時刻了。

1.小組交流

師：拿出我們的錯題集，看看自己整理的錯題以及“我是小問號”部分，還有哪些不理解的地方嗎？先在小組里解決，小組內不能解決的，一會兒再全班交流討論。（上圖是學生錯題集的部分內容）

小組交流、討論。

2.全班討論

師：還有哪些問題需要全班討論的？或者雖然你們已經解決了，但覺得這個問題也值得全班分享？

生14：71+29=x，這是不是方程？

生15：10-（ ）=2是不是方程？

生16：20÷x=4，這個方程怎么解？

師：我們來整理一下，這三個問題大概可以分成兩類，一類是“是不是”方程的問題（板書：是不是），一類是“怎么解”方程的問題（板書：怎么解）。我們一個一個來研究討論。

師：我們先看第一個問題，認為它是方程的舉手。（大部分同學舉手）

師：認為它不是方程的舉手。（4個同學舉手）

師：來吧，都來說說理由吧。

生17：71+29=x不僅是等式，而且還含有未知數，所以它是方程。

生18：不對，這個x沒有意義。

生19：可它是含有未知數的等式呀！

生20：我們可以把x用手蓋住，發現71+29已經是一個完整的算式了，所以這個x完全沒有用。

師：咦，我們可以讀一讀其他幾個方程，來體會體會他們所說的“沒有意義”和“沒有用”。

生齊讀：3+x=10，x÷9=90，x-54=18。

師：跟這幾個方程比，（指71+29=x）這里的未知數x有什么特殊的呢？

生21：這里的x單獨在右邊，而其他的方程中，未知數跟已知數在一起的。

師：是啊，在這些方程里（指剛讀的3個方程），未知數與已知數是平等的，未知數也參與了列式；而在71+29=x中，x待在等號后面不干活。

生20：所以我認為這個未知數x根本沒有意義，71+29=x也就不能算是方程。

師：知道嗎？關于這是不是方程的問題，老師們也一直爭論不休，張老師在自己的QQ空間里轉載了很多專家的說法，也寫了自己的一些思考，同學們想閱讀嗎？

生齊：想！

師：建議大家在閱讀前、閱讀后都要有自己的思考，形成自己的觀點。但有一點我們必須承認，正如剛才大家所說的，在71+29=x中，未知數x沒有意義、沒有用，所以以后我們自己列方程解決實際問題時，盡量不要列成這個樣子。

師：再來看第2個問題，10-（ ）=2是方程嗎？

生22：是方程，因為“（ ）”也可以表示未知數，所以這是含有未知數的等式，而且這個未知數還參與列式了。（全班掌聲）

師：最后一個問題，怎么解方程20÷x=4？大家試試看吧。

（學生嘗試解方程后交流）

生23：我是根據等式的性質來解的。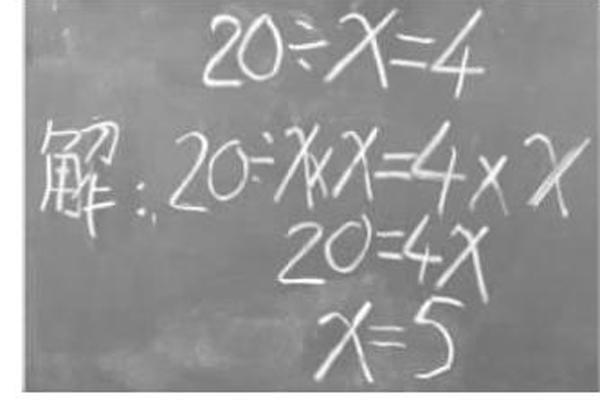

師：他的解法跟我們以前的解法有什么不一樣？

生24：這種解法也是利用了等式的性質，但是以前都是在等式的兩邊同時加、減、乘、除以同一個數，而這里是同時乘x。（掌聲）

生25：我是根據未知數的位置來解的。未知數是除數，所以就等于20÷4。

生26：我還有一種方法，我在等式的兩邊同時除以4，這樣方程就轉化成5÷x=1，這樣就知道x=5。

師：這么多不同的方法，大家覺得有什么相同的地方嗎？

生25：不管哪種方法，都是想辦法讓方程的左邊只剩下x。（掌聲）

師：解決了“是不是”與“怎么解”的問題，我們再來研究“為什么” （板書：為什么），為什么要學方程呢？

生27：方程可以解很多難題呢。

師：關于方程的魅力我們可以一起來體會。我們來進行一個小競賽。當屏幕上的題目出示完畢，我們比一比，誰最先舉手，能用方程表示題目的數量關系。

屏幕顯示：今天早上，8路公交車從江蘇路站出發時，車上有x人。到傅佐路站時，下去4人，上來6人；到西流灣公園站時，又下去5人，上來9人。這時，車上有12人。那么從江蘇路站出發時，車上有多少人？

（題目出示完畢，幾乎全班舉手）

生28：x-4+6-5+9=12。（全班掌聲）

師：這么復雜的數量關系，你們是怎樣又快又對地列出方程的呢？

生29：我們只要按著題目的意思順著寫就行了。

師：多形象的一個詞啊！“順著寫”，知道嗎？“順著寫”是方程最大的魅力！

師：關于方程的魅力我們繼續來體會。

屏幕顯示：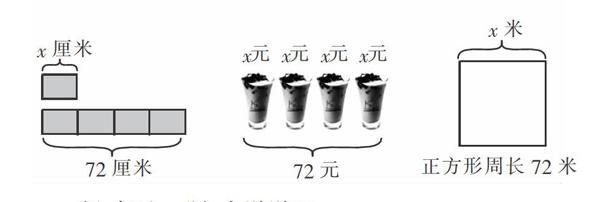

師：任選一題，來說說吧。

生30：我選第3幅圖，4x=72。

生31：我選第1幅圖，4x=72。

生32：我選第2幅圖，4x=72。

師：咦，圖不同的呀，為什么列出的方程卻相同呢？你還能試著編一道用4x=72表示的題目嗎？

生33：小芳每天看書x頁，4天看了72頁。（掌聲）

生34：四個同學都有x張郵票，一共有72張郵票。

（還有很多同學繼續舉手）

師：這樣的問題能編得完嗎？

生齊：編不完。

師：是啊，一道方程竟然可以表示無數個問題，一個方程竟然有如此強大的概括性，這也是方程的魅力。

四、考考自己

師：真誠地祝賀大家在分享的同時，又有了那么多的體會與收獲！最后，讓我們來“考考自己”。學習單的反面，獨立完成。

1.看圖分析數量關系，并列方程解答

2.看圖列方程，不用解答

一瓶800毫升的果粒橙，正好倒滿5個小杯和1個大杯。

課后思考：

周國平說：“教育不是制造，學生不是產品。所以衡量教育質量，不可能用外在的需要、外在的目的來制造機械產品，來制定指標，用指標來衡量。所以，要提高教育質量，一個前提就是把學生當成人，了解學生的生長，對他們的培育處于什么樣的狀態。”如果說我們要真正做到教育目標上以人為本，教學方式上人性化，那么學生在中央的數學課堂不僅是一種境界，更是一種積極狀態。

學生在中央的數學課堂，首先把學生看成一個真正的人。把學生當成人性意義上的人，讓他在數學學習中體會到人性的豐富、做人的尊嚴、做人的快樂，享受數學學習的樂趣，從而得到更大的發展；其次關注個性的發展，把每個學生看成獨特的個體，讓他最好的稟賦能夠顯示出來，得到發現，得到發育。

《“方程”分享會》是在學生學完“等式和方程”“等式的性質與解方程”后的一節練習課，但它又與一般的練習課稍有不同，是讓學生以分享的形式進行自主交流與自覺練習，并在自由分享的過程中提升認知的一節“學生在中央”的數學課堂。值得一提的是，這樣的課型不是公開場合的作秀，“分享會”“經驗發布會”“講評會”等一系列課型，是我們瑯琊路小學開發的數學常態課堂。“分享會”所呈現的一些課堂環節也是平時課堂的一些常態動作，如“數學分享”時刻、“我是小問號”時刻，等等。

在今年3月3日舉行的南京市小學數學教學現場會上，本課向全市的領導、教師開放，南京市教研室朱宇輝主任評價：這是一堂表達學生學習力的數學課，更是一堂提升學生學習力的數學課。《“方程”分享會》絕不是一堂精雕細琢的課，甚至不是一堂可以“試上”與復制的課，說得更直白些，它就是一堂學生在中央的數學裸課，為什么能得到專家的贊嘆呢？我想這也正應了“最常態的課便是最好的公開課”這句話。

認真思考本課，以下幾點表達了學生在中央的教學理念：

1.學習經驗源自于學生的真切感受——真分享

課開始時的“熱情分享”，學生始終以“主人”的角色參與活動。小組分享時，學生們圍繞主題輪流說自己的認識與學習體會。每個同學既要說清楚自己的體會，還要聽懂別人的認識，最后還要綜合本小組的經驗，以便全班分享。我們看到：有的小組在組內分享時有相互糾錯的過程，有的小組有相互質疑的行為，更多的是相互補充與提醒。小組分享彌補了教師無法面面俱到的缺憾，讓課堂里所有的聲音都得到了關注與承認，同時也鍛煉了學生彼此聆聽的能力。

在“全班分享”時，同學們又呈現了屬于他們的精彩。“我們小組認為，等式就是含有等號的式子，而方程是含有未知數的等式。”“如果我們把世界上所有的等式都放在這個口袋里，那方程應該在哪呢？”“不管是用等式的哪個性質來解方程，其實都是為了讓方程的左邊只剩下‘x，就得出方程的解了。”……學生們的語言是稚嫩的，也許還不夠完美、不夠科學，但它們卻是學生們自己的真切感受，是學生們自己的獨特體驗。

學生在前幾節課的學習中，只是初步學會了解方程，如何幫助他們掌握解方程的方法，形成相應的技能呢？在一般的課堂里，一定有老師的說教，可在這里只有學生彼此之間的分享。英哲同學的解法跟大家不一樣，英哲分享說：我是這樣想的，在等式的兩邊同時乘9，那么左邊“÷9”跟“×9”正好可以抵消，所以我就把它們想在心里，直接寫x=90×9。老師抓住“想在心里”這一策略，使解方程的過程更加算法化。同學們通過比較、評價不同的方法，在算理與算法并行的同時，掌握了解方程的技能，讓解方程的過程更簡潔，讓解方程的思考更加流暢，也與中學里解方程的“移項”等方法相接軌，有利于提升解方程的能力。

正因為分享的學習經驗都是學生的親身體會，所以在整個“熱情分享”時刻，課堂氛圍始終如此輕松、自然、平等，學生不必嚴肅拘謹，沒有正襟危坐，有的只是愉快的分享、此起彼伏的掌聲和彼此會心的笑臉。學生真正地站在了課堂的中央，真實地擁有了一個樂于表達的課堂、促進自我內在對話的課堂。

2.研究問題源自于學生的真實疑惑——真研究

在質疑問難環節，同學們首先以自己的錯題集為載體，根據整理的錯題及記錄的“我是個小問號”內容，開展自我剖析與互相幫助的小組活動。有的同學在小組里坦誠地說出自己的錯題經驗，有的同學在小組里尋求幫助，也有的同學相互一起交流、爭論著某一問題。此時，每個學習小組都是一個學習共同體，每個同學都能在小組里實現自己的價值，并獲得看得見的生長。

學生以主人的姿態交流自己的學習，包括自己的問題與疑惑，有些疑惑在小組內得到了解決，也有些疑惑小組內不能解決，于是就有了全班討論。在全班討論階段，同學提出了“71+29=x”與“10-（ ）=2”是不是方程的問題，還提出了怎么解方程20÷x=4的問題。對于學生提出的問題，教師沒有只是作出簡單的解答，或者是蒼白的說理，而是依然讓學生站在課中央，把話語權給學生。學生對于71+29=x是不是方程的問題，盡管有兩種不同的意見，但在學生的爭論中，我們驚喜地看到學生對于方程內涵的理解：方程不僅僅是含有未知數的等式，更是把未知數擺到與已知數同等的位置參與列式。

學生在中央的數學課堂的關鍵是體現“人”與“人性”，“71+29=x”是不是方程的問題是教育界一直爭論的問題，教師沒有回避，而是選擇了直面，更是在學生爭論后，善意地告訴學生，教師在自己的QQ空間里寫了關于這個問題的思考，并轉載了許多專家的觀點，引導學生去再閱讀、再思考，形成自己的觀點。學生與教師是如此地平等，包括機會的平等、表達的平等、精神的平等……學生的學習不會因為40分鐘的結束而停止，學生在中央的數學課堂是促進學生41分鐘發展的課堂。

無論是對于“是不是”方程的問題，還是“怎么解”方程的問題，因為都是學生自己的真實疑惑，也就有了學生全身心的投入與熱情，學生始終以小主人的姿態主動、自覺地研究問題。

3.學習習慣源自于學生的真情經歷——真養成

數學學習一直強調良好的學習習慣，可良好的學習習慣哪里來？一定不是僅憑單調的說教就能形成的。本課學習中，學生表現出了優秀的學習習慣，包括課堂學習習慣與課后作業、思考習慣等。具體如錯題整理的習慣，及時記錄問題、研究問題的習慣，合作學習、相互質疑、懂得分享的習慣，等等。

課上完后，聽課老師們紛紛上來，查看學生的錯題集，發現我們學生的錯題集上有與眾不同的一欄，那就是“我是個小問號”部分，同學們會在這一欄里隨時記錄自己的問題，以便共同研究與探討。聽課老師們還索要了學生們的課堂學習單，發現學生在課堂學習時，善于用自己的方式記錄自己的思考，愿意把自己的思維過程展示給自己的同伴。

聽課老師們疑惑：為什么這些學生擁有如此好的學習習慣呢？沒有更多的理由，這些都只是同學們的日常行為，也許一開始還有些制度化的成分，可當學生們親身經歷，品嘗到學習的快樂與成功的喜悅后，這些“習慣”也就成為學生們自己最自然的需要與最真實的學習品質了。

最后，值得一提的是：學生在中央的課堂并不是教師不作為的課堂，而是對教師提出了更高的要求，要求教師有更智慧的作為。如在本課的質疑問難階段，學生們提出了“是不是”與“怎么解”的問題，老師在此基礎上又提出了“為什么”的問題。通過一系列的真實經歷，學生真切體會到了方程“順著寫”的魅力，也感受到了方程是一種模型的思想，認識上了一個層次。

張奠宙教授認為，數學的核心素養有“真、善、美”三個維度，而本課的“真分享”“真研究”“真養成”，旨在引領學生以學習小主人的角色自覺探索數學真理、熱情感受數學思想方法、主動欣賞數學智慧之美，幫助學生提高數學學習力，逐步擁有數學品質，并最終形成數學素養。

綜上所述，學生在中央的數學課堂是兒童的數學課堂：課堂不再“秀”教師，而是兒童自由表達的舞臺；課堂不再是戲場，只追求精致美、流暢美、細膩美，而是更關注學生體驗解放感、震撼感、力量感；課堂不再只是教學內容的落實，而是對數學的快樂享受，更是兒童生命的美妙拔節！學生在中央的數學課堂指向兒童的數學核心素養，促進兒童的生命成長，它著力表達了數學課堂教學的理念：打造第一人稱視角的課堂，快樂的課堂，促進41分鐘發展的課堂。？筻