“一圖多變”巧解題

尹蕾

[摘 要] 中考命題常考常新，但揭開考題的神秘面紗，不難發(fā)現(xiàn)表面看似不同的問題，卻有相同的本質(zhì). 本文以歐幾里得《幾何原本》中一種證明勾股定理的方法為引例，將其靈活應(yīng)用解決中考問題.

[關(guān)鍵詞] 勾股定理；三角形全等；正方形；矩形

著名的古希臘數(shù)學(xué)家歐幾里得在其巨著《幾何原本》中給出了勾股定理的一種證明方法：

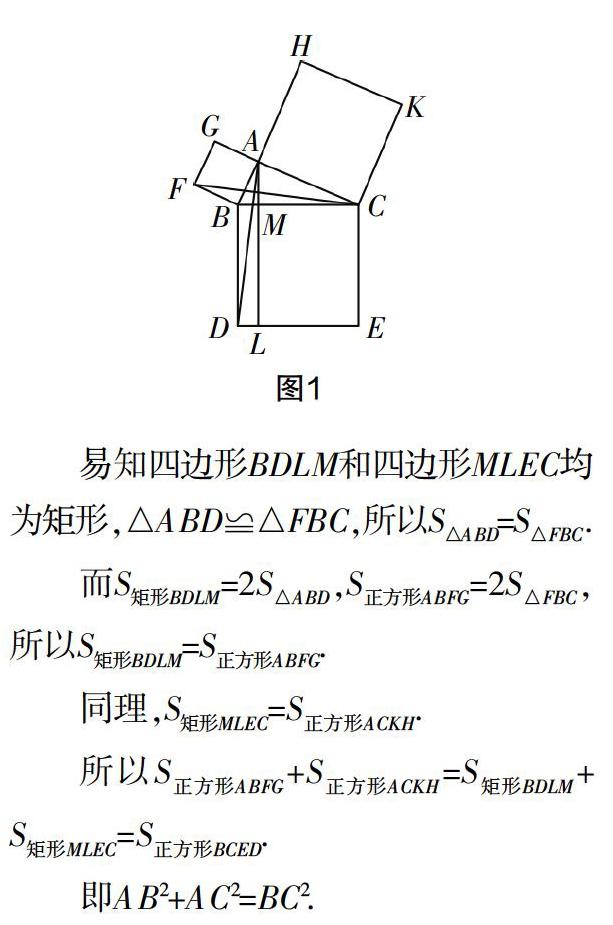
如圖1，分別以Rt△ABC的直角邊AB，AC及斜邊BC為邊向外側(cè)作正方形ABFG、正方形ACKH和正方形BCED，連接CF，AD，作AL⊥DE分別交BC，DE于點(diǎn)M，L.

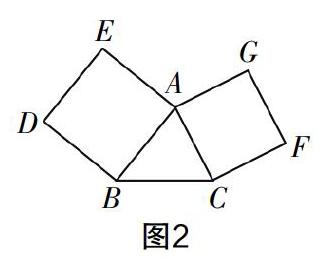
如果將圖1中的直角三角形變成一般三角形，以三角形的三邊為邊作正方形變?yōu)橐詢蛇厼檫呑髡叫危瑫?huì)得到這樣一個(gè)圖形：如圖2，分別以△ABC的兩邊AB，AC為邊向外作正方形ABDE和正方形ACFG.

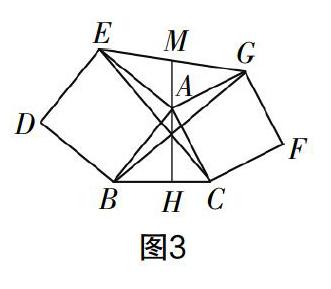
圖2同圖1相比，將直角三角形變成一般三角形，弱化了對(duì)三角形形狀的限制，同時(shí)減少了一個(gè)正方形，顯得簡(jiǎn)單大方，備受中考命題者的青睞.瀏覽近年的中考試卷，筆者發(fā)現(xiàn)很多形式新穎、具有一定的啟發(fā)性和挑戰(zhàn)性的試題都是在圖2的基礎(chǔ)上演變而來的，值得關(guān)注和研究.下面以例題說明圖2及其變式在中考中的應(yīng)用.

綜上，數(shù)學(xué)問題因變化而精彩，對(duì)于一道貌似很簡(jiǎn)單的題目，通過合理的改編，往往可生成一些具有豐富內(nèi)涵的創(chuàng)新問題，并以此來激發(fā)學(xué)生的解題思維，培養(yǎng)其解題能力. 本文靈感來自于勾股定理的一種古老的證明方法，通過深入探究，挖掘出方法背景后隱藏的本質(zhì)，并將其原理應(yīng)用于數(shù)學(xué)問題的求解中.