例析與導數相關的參數問題

☉江蘇省海門實驗學校劉九華

例析與導數相關的參數問題

☉江蘇省海門實驗學校劉九華

導數和含參數函數的單調性問題是歷年高考命題的熱點，也是難點.試題主要有以下兩類：一是利用導數解決有關含參數函數的單調性問題；二是已知含參數函數的單調性求參數范圍的問題.下面筆者結合平時的教學實踐談談這兩類問題，歡迎指正.

一、利用導數解決含參數函數的單調性問題

利用導數解決含參數函數的單調性問題是常考題型，傳統解法要求考生的思維極其嚴密才能討論全面.筆者根據教學經驗，要解決這類問題，首先明確討論的三個基本點:1.導函數是否存在零點；2.若導函數存在零點，零點是否在定義域內；3.若導函數有零點，零點是否相等.有時可能是上述幾種因素的綜合考查，下面舉例說明.

①當a＜0時，由f′（x）=0，解得x=a或x=1，a?（0，+∞），在（0，1）上，f′（x）＜0，在（1，+∞）上，f′（x）＞0，故f（x）的單調遞減區間是（0，1），單調遞增區間是（1，+∞）.

②當a=0時，f′（x）=x-1，在（0，1）上，f′（x）＜0，在（1，+∞）上，f′（x）＞0，故f（x）的單調遞減區間是（0，1），單調遞增區間是（1，+∞）.

③當0＜a＜1時，在（0，a）和（1，+∞）上，f′（x）＞0，在（a，1）上f′（x）＜0，故f（x）的單調遞增區間是（0，a）和（1，+∞），單調遞減區間是（a，1）.

⑤當a＞1時，在區間（0，1）和（a，+∞）上，f′（x）＞0，在區間（1，a）上f′（x）＜0，故f（x）的單調遞增區間是（0，1）和（a，+∞），單調遞減區間是（1，a）.

綜上所述：當a≤0時，f（x）的單調遞減區間是（0，1），單調遞增區間是（1，+∞）；

當0＜a＜1時，f（x）的單調遞增區間是（0，a）和（1，+∞），單調遞減區間是（a，1）；

當a=1時，f（x）在（0，+∞）上單調遞增；

當a＞1時，f（x）的單調遞增區間是（0，1）和（a，+∞），單調遞減區間是（1，a）.

點評：此例導函數有零點，但需考慮零點是否落在定義域內與導函數有零點但需要討論零點是否相等的問題的結合.解題中抓住主要問題，確定分類標準，逐步擊破，才能快速、正確地解題.

二、已知函數單調性利用導數求參數范圍問題

已知函數單調性，求參數范圍是高中數學重點考查的題型之一.關于此類問題在各類高考題中經常出現，變化也多.那么如何簡單、準確地解決這類問題呢？一般有以下幾種思路可以考慮.

（一）分離參數法

故a的取值范圍是a≥3.

點評：若a≥f（x）對x∈D恒成立，則a≥f（x）max；若a≤f（x）對x∈D恒成立，則a≤f（x）min.求函數的最值一般要用到函數的單調性.

（二）數形結合法

例3已知函數f（x）=lnx-a2x2+ax（a∈R）在區間（1，+∞）上是減函數，求實數a的取值范圍.

解法1：因為f（x）是區間上（1，+∞）減函數，

所以f′（x）≤0在上（1，+∞）恒成立.

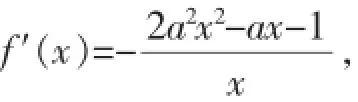
即2a2x2-ax-1≥0在（1，+∞）上恒成立.但此時無法分離參數a，分離參數法不奏效.因為2a2x2-ax-1≥0在（1，+∞）上恒成立，令g（x）=2a2x2-ax-1，

當a=0時，-1＜0，故a=0不滿足題意.

當a≠0時，2a2＞0，Δ=9a2＞0.

故由二次函數圖像，數形結合知，

（三）分類討論法

點評：當無法分離參數時，可用分類討論法求參數的取值范圍.但是，若導函數與二次函數有關，用數形結合法能更簡便、快速地解決問題，比分類討論法更方便.

在每年的高考試題中都會出現與函數單調性、導數有關的問題.掌握了以上兩種題型及常規處理方法，才能對新穎題型的處理游刃有余，同時能培養學生思維的深刻性和靈活性.G