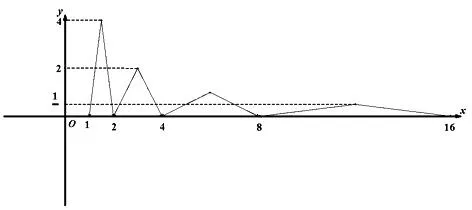
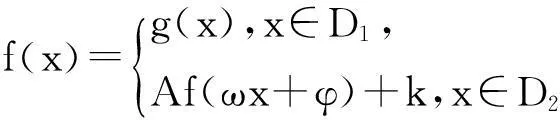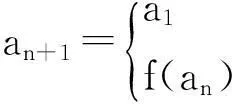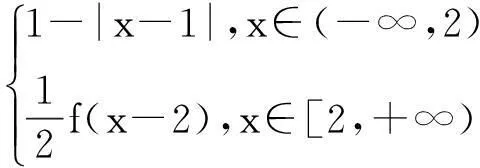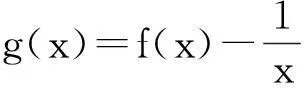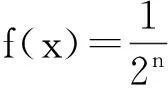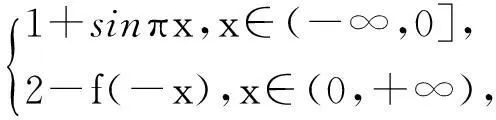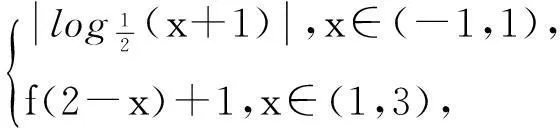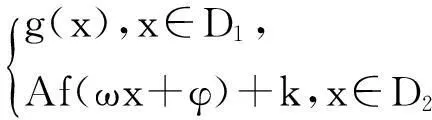一類“顯隱混搭型”分段函數的圖像及其應用
——以零點相關問題為例

浙江省衢州第二中學　(324000)　傅建紅

?

一類“顯隱混搭型”分段函數的圖像及其應用
——以零點相關問題為例

浙江省衢州第二中學(324000)傅建紅

一、策略分析

我們知道，圖像法是解決函數零點相關問題的重要手段，但本題中這類函數將如何作圖？讓我們從分析f(x)的構成入手：因為當x∈D1時，f(x)=g(x)，即f(x)在D1上的圖像已定；但當x∈D2時，f(x)=Af(ωx+φ)+k，故f(x)在D2上的圖像未能直接給定.然而，y=f(x)與y=Af(ωx+φ)+k的圖像之間有著“天然”的聯系，所以我們只要以f(x)在D1上的圖像為起點，一步一步的往上“攀”(拾級而上)，即可作出f(x)在D2上的圖像.為明晰圖像由來，先給出如下性質：

性質1(平移變換) 設f(x)=

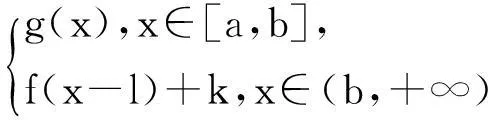
證明：因為當x∈[a,b]時，有f(x)=g(x)，所以當x-l∈[a,b]，即x∈(a+l,b+l]時，有f(x-l)=g(x-l)(迭代)，由于(a+l,b+l]?(b,+∞)，所以f(x)=f(x-l)+k=g(x-l)+k；再當x-l∈[a+l,b+l]，即x∈(a+2l,b+2l]時，f(x-l)=g(x-2l)+k(再迭代)，因為(a+2l,b+2l]?(b,+∞)，所以f(x)=f(x-l)+k=[g(x-2l)+k]+k=； …；以此類推，故當x∈(a+nl,b+nl](n∈N)時，f(x)=g(x-nl)+nk得證.

說明：由性質1的證明過程可知，此時分段函數f(x)可以寫成

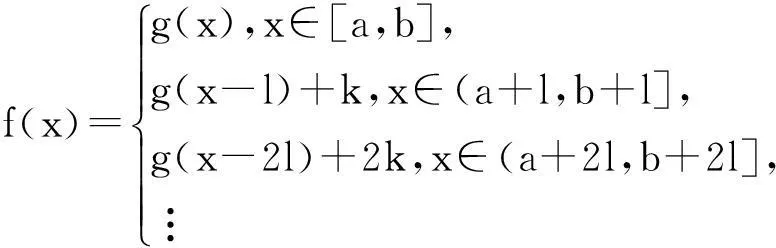
性質2(伸縮變換)設f(x)=

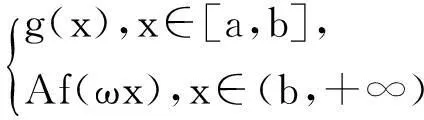
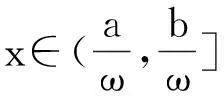
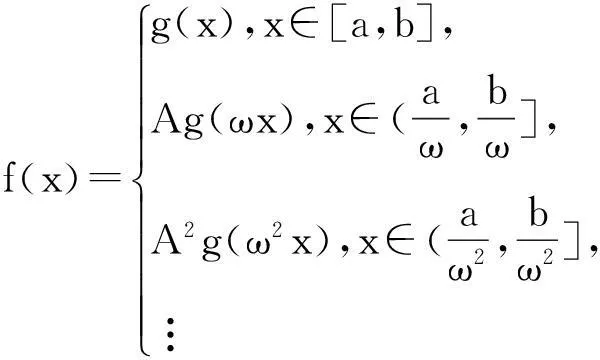
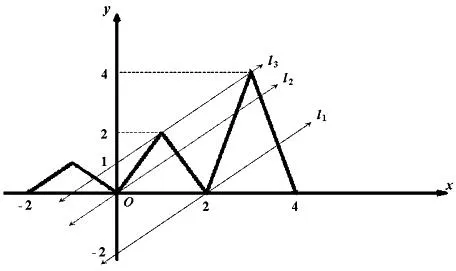
性質3(對稱變換) (1)設f(x)=

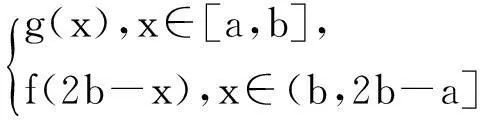
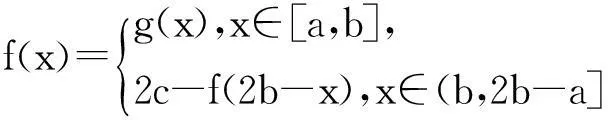
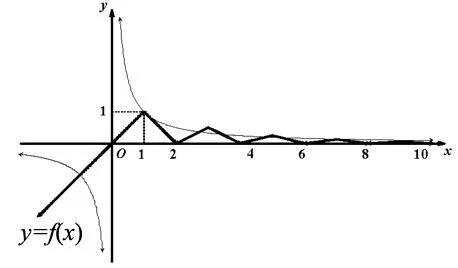
(其中a

證明：(1)因為當x∈[a,b]時，有f(x)=g(x)，所以當2b-x∈(a,b]，即x∈(b,2b-a]時，有f(2b-x)=g(2b-x)(迭代)，所以f(x)=f(2b-x)=g(2b-x).

(2)證明同(1)，略.

說明：由性質3知，函數f(x)在區間(b,2b-a]上的圖像可由f(x)在[a,b]上的圖像關于直線x=b(點(b,c))對稱得到.

評注：(1)性質1僅考慮了l>0且k>0時的平移變換，性質2僅考慮了A>1且0<ω<1下的伸縮變換，而性質3僅考慮了函數在連續區間上的對稱變換，其它情形下的變換性質可由讀者自行推導；

二、應用舉例

(1)零點個數問題

例1設函數f(x)=

A.4B.5C.6D.7

圖1

變式1定義在[1,+∞)上的函數f(x)滿足：(1)f(2x)=2f(x)；(2)當2≤x≤4時，f(x)=1-|x-3|.則函數g(x)=f(x)-2在區間x∈[1,28]上的零點的個數為(答案：4)

(2)零點之和問題

A.3n2+3nB.3×2n+2+9

C.3n+2+6D.9×2n+1-3

圖2

變式2已知函數f(x)=

(3)參數范圍問題

例3已知函數f(x)=

區間[-2,4]內有3個不同實根，則實數a的取值范圍是().

A.(-2,0)B.(-2,0]

C.(-2,0)∪(1,2)D. (-2,0)∪{1}

圖3

解:方程f(x)=x+a在區間[-2,4]內有3個不同實根，即函數y=f(x)(x∈[-2,4])圖像與動直線l:y=x+a在同一坐標系下有3個不同的交點.先作y=f(x)的圖像：作函數y=1-|x+1|(x∈[-2,0])的圖像→將所得圖像向右平移2個單位再縱向伸長為原來的2倍→重復這兩個動作，即得函數f(x)圖像(如圖3)；然后作直線y=x+a.觀察圖像易知：當動直線l平移至l1與l2之間以及在l3上時，兩圖像有3個交點.易知a為直線l在y軸上的截距，所以a∈(-2,0)∪{1}，故選D.

變式3已知函數f(x)=

說明:不難看出，上述三例的命題手法如出一轍(均以混搭函數為背景，考察函數零點相關問題)，其解題思想也完全一致(數形結合)，因此，只要能作出函數(尤其是混搭函數)的圖像，即可為后續解答鋪平道路.限于篇幅，本文變式只給出答案.

綜上，本文通過函數迭代，揭示了f(x)=

參考文獻

[1]應立君,余雪贊.例說函數圖像的變換[J].中學教研(數學),2014,7.