用求多元函數最值的一般方法解一道競賽題

四川省成都市石室中學　(610106)　蔡遠林

?

用求多元函數最值的一般方法解一道競賽題

四川省成都市石室中學(610106)蔡遠林

文[1]指出,在中學里求多元函數M=F(x,y,z)的最值,常用兩種方法,一是特殊的減元法,即化為一個或兩個自變量的函數M=f(t),其中t=G(x,y,z);或M=g(u,v),其中u=h(x,y,z),v=r(x,y,z).二是一般的逐步推進法,即把其中一個變量視為自變量(如z),其余變量視為常數(參數),先求關于z的函數f(z)的最值g(x,y),再求g(x,y)的最值.求g(x,y)的最值又重復上述過程.本文用文[1]的上述方法給出一道全國競賽題的多種解法.

注：為節省篇幅，以下解法2-6均略去不等式取等號的敘述.

解法4:在方程組

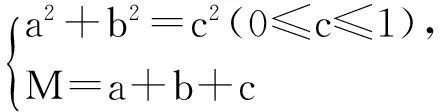
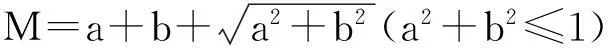
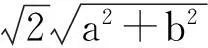
參考文獻

[1]熊福州.由2010年高考四川理(12)看多元函數最值問題的解法[J].中學數學研究(江西)，2010,10.