用“區間的存在性”求解一類恒成立問題

江蘇省東臺市安豐中學　(224221)　徐建華

?

用“區間的存在性”求解一類恒成立問題

江蘇省東臺市安豐中學(224221)徐建華

不等式恒成立問題是高中數學中非常重要的一類問題，它通常涉及到函數、不等式、導數等高中數學的主干知識，因而在高考中有十分重要的地位，是高考數學的高頻考點，并且一些不等式恒成立問題還常以壓軸題的身份出現.

不等式恒成立問題可化為下列一般形式：若關于x的不等式f(x,a)≥0(或≤0)對任意x∈[m,n]恒成立，試求實數a的取值范圍.在此基礎上，有一類特殊的恒成立問題，我們容易發現不等式的取等條件：當x=m時，等號成立，即f(m,a)=0.怎樣解決這一類特殊的恒成立問題呢？筆者有一個統一的解題思路，利用區間的存在性求解，上述的取等條件說明，存在實數x0>m，使得函數f(x,a)在(m,x0)單調遞增(或單調遞減)，由此可求參數a的取值范圍.本文試舉幾例，說明這種解題方法在處理此類特殊恒成立問題的普適性.

例1(2010年新課標全國卷(理)第21題)設函數f(x)=ex-1-x-ax2.

(1)略；(2)當x≥0時，不等式f(x)≥0恒成立，求實數a的取值范圍.

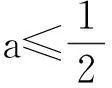
(1)求a,b的值；

若去分母，則當x>1時，有φ(x)=(k-1)x2+2xlnx-k+1<0；當00.注意到x=1時，φ(x)=0，于是先考慮任意x∈[1,+∞)，不等式φ(x)≤0恒成立.這說明存在實數x1>0，使得函數φ(x)在(1,x1)上單調遞減，所以φ′(x)=2(k-1)x+2(lnx+1)≤0在(1,x1)恒成立.由φ′(1)≤0，得k≤0.

同理，由x∈(0,1]時，不等式φ(x)≥0恒成立，也能得到k≤0.

例3(數學通訊“我為高考設計題目”題139的改編題)已知函數f(x)=ex，g(x)=mx+n.

(1)略；(2)若對任意x∈(-1,+∞)，恒有

|f(x)|≥|g(x)|成立，求實數m的取值集合.

最后，我們再來反思這類恒成立問題的設計思路：不等式通常是由兩個基本曲線y=f(x)與y=g(x)構成，兩曲線相切于橫坐標為a的點，其中曲線y=g(x)的方程中設有參數m，但它們的公切線性質不變；然后再以a為端點的某個區間[a,b)(或(b,a])中，滿足f(x)≥g(x)(或≤)恒成立，從而要考生求參數m的取值范圍.在例1中，容易驗證y=ex與y=ax2+x+1相切于點(0,1)，為使ex≥ax2+x+1在[0,+∞)恒成立，可求參數a的范圍.

其實，本文中用區間的存在性解題的原理很簡單，如f(x)≥g(x)在[a,b)上恒成立，因f(a)=g(a)且f′(a)=g′(a)，在以a為端點的右側附近，函數f(x)的上升速度要快于g(x)，所以存在區間(a,x0)，使得f′(x)≥g′(x)，即h′(x)=[f(x)-g(x)]′≥0在(a,x0)上恒成立，并且h′(a)=0，還可以再次使用區間存在性.

參考文獻

[1]佟成軍. 我為高考設計題目，題139[J]. 數學通訊，2014.7：60-61.

[2]吳彤. 從歸納猜想到試題設計[J]. 數學教學研究，2014.10：47-50.