匯率波動性的近似熵與樣本熵分析

劉慶丹 李久華 楊會杰

摘 要：熵估計在生理時間序列上被廣泛應用，例如近似熵與樣本熵。將熵估計方法應用于匯率時間序列中，用于識別匯率市場在不同時間的波動狀態并加以分析。在不同維度下討論了近似熵與樣本熵反映匯率時間序列波動的情況，并對同一維度下近似熵與樣本熵效果進行了比較，發現樣本熵比近似熵可以更好地反映匯率的波動性，并且更加靈敏。得出樣本熵算法在匯率市場中良好地反映了大事件的發生與延續，解決了近似熵算法對微小的復雜性變化不靈敏的缺陷，并且顯著提高了熵估計在短時間序列上的可用性和精確度。

關鍵詞：匯率；波動性；近似熵；樣本熵

中圖分類號：F 822 文獻標識碼：A 文章編號：1672-7312（2016）04-0438-04

0 引 言

近年來，金融時間序列分析已經越來越受到人們的關注[1-2]。中國匯率市場作為一個發展中市場，其規則、效率、結構等方面還不夠規范、有效、成熟。因此，實證研究匯率等金融時間序列的波動情況，對分析金融時間序列的內涵具有重大意義[3]，并對我國經濟產生了很多積極影響，例如，對貿易伙伴的合作關系可以進行有效的緩解作用，還可以促進我國加快調整產業結構；當然也有不少人提出了由于人民幣兌美元的數值上升而導致的抑制外來資產以及外匯儲備大幅縮水等消極影響[4]。

1865年，德國物理學家R.E.Clausius在提出熱力學第二定律后的第15年，第一次引入了熵的概念，并且利用熵增加原理來重新定量闡明了熱力學第二定律。此后的30多年，熵得到了非常廣泛的應用和發展，先后出現了由Boltzmann提出的統計熵，由Shannon提出的信息熵，由Pincus提出的近似熵，由Richman提出的樣本熵[5]。從此熵估計就成為了物理學中的一個非常有意義的概念并逐漸滲透到某些社會科學、生命科學、信息論、甚至宇宙學中[6]。

金融時間序列是非平穩、非線性的時間序列，具有序列長度比較短、價格的變化無序不平穩、其他不可控干擾因素較多等特點[7]。近幾年來，近似熵（approximate entropy，下文簡記為ApEn）與樣本熵（sample entropy，下文簡記為SampEn）分析方法在解決由于上述序列而出現的問題時發揮了非常重要的作用。近似熵分析方法由 Pincus[8]在k-s熵改進得來的，k-s熵對序列長度有很大的依賴性，而近似熵改進了這一點，即對于有些短的時間序列，也可以得到有效可利用的結論，因而在實證研究金融時間序列特征中有非常多的應用。ApEn（m，r，N）是對相似容限為r，時間序列長度為N的時間序列，在m點數據互相相似情況下m+1點數據互相相似的條件概率CP的負平均自然對數的近似值，因此近似熵是一種標度不變的方法。

從近似熵的算法可以看出，近似熵的定義中存在著對自身數據段的匹配，以至于它無法對對很小的復雜性變化進行有效的解讀。因此，需要改進此種方法來克服這種偏差產生的影響，即要消除自身匹配。

樣本熵分析方法是由Richman等在基于近似熵的基礎上改進來的，近幾年得到了越來越多的接受、關注與認識，被廣泛應用于生物、臨床、金融、醫學等領域[9]。相對于近似熵而言，樣本熵不包括自身數據段的匹配，計算方法也不需要很長的數據長度，具有更好的相似性、一致性，由于數據丟失而產生的問題也不敏感。

1 近似熵與樣本熵

近似熵是近些年來才發展起來的一種可以度量時間序列復雜性和統計量化的規則。它是在20世紀90年代初由Pincus為了克服在混沌系統中求解熵特別麻煩才提出的。

近似熵是對非線性時間序列復雜性的一種非負的定量描述，它對于相對較短的（大于100個數據點）、含噪聲的時間序列進行計算分析，使其顯示出潛在的應用價值，這是由于產生近似熵的主要的技術思想是：它并不是試圖完全重新構造吸引子，而是用一種簡單且有效的統計方式——邊緣概率分布的不同來區分各種不同的運動過程，其中吸引子是一個數學上的概念，用來描寫運動的收斂類型；邊緣概率在數學概念中是指當實驗所獲取的事例按不同的標準進行分類時，忽略掉某些分類標準而只考慮在某一種分類標準下某事件出現的概率。

參數m和r的選擇非常重要，如果m過大或者r過小，小于閾值r的匹配數會過少；同時，如果m過小r過大，所有的模版都匹配。Pincus建議當數據長度N為100到5 000時，m一般取1或者2，r取0.1到0.25倍的序列標準差。但是這個建議對不同的數據集并不總是能得到最優的結果。下面結合matlab程序來說明近似熵的算法步驟。

樣本熵是由Richman提出的一種新的時間序列復雜性測度方法[10-11]。它是由近似熵改進而來的，用意于消除近似熵由于自身匹配而造成的計算偏差，彌補其對微小的復雜性變化不靈敏的缺陷，是一種比近似熵精度更好的方法。樣本熵的計算步驟如下

SampEn（m，r，N）=-lnBm+1（r）/Bm（r）」.

樣本熵的物理意義與熱力學熵相同，主要用來定量刻畫系統的復雜度或無序性。樣本熵值越低，序列自我相似性越高，產生新模式的概率越低，時間序列越簡單； 反之，樣本熵值越高，序列自我相似性越低，產生新模式的概率越高，時間序列越復雜。

2 實證分析

文章搜集了從1994年1月10日至2014年12月31日人民幣兌美元的匯率，共5 477個數據，由于每一年都會有一個近似熵值和樣本熵值，所以將每一年的數據修正成為同等長度的時間序列，即將在同等時間位置上存在缺失數據就將此時間點全部刪除，于是就得到了從1994年到2014年每年都有256個數據點；為了消除不同數據之間的量差，在數據分析過程中，所采用的數據為1994年1月10日至2014年12月8日共21年的人民幣兌美元的匯率一階差分數據，如圖1所示。通過近似熵與樣本熵方法，來分析中國匯率市場不同時間上的復雜性特點，并進行比較。

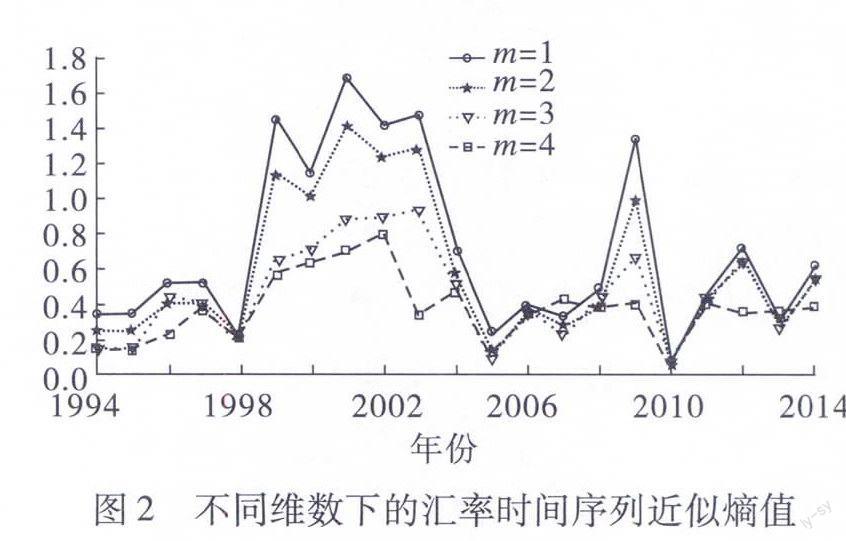
圖1 匯率一階差分數據利用matlab得出從1994年到2014年的近似熵，并畫出了m=1到m=4不同維度下匯率時間序列近似熵的變化趨勢，結果如圖2所示。我們從中可以看出近似熵值在1998年、2004年、2005年、2010年發生了驟降。但是2000年的美國新經濟危機，2001年的“9·11”恐怖襲擊事件，2008年的環球金融危機從圖2的近似熵值并不能顯現出來，所以在很大程度上近似熵并不能很好地說明匯率的波動性；并且不同維數下近似熵值變化明顯，說明近似熵值與數據的個數有很大的關聯，數據量越大近似熵值越小，所以在數據量小于一定程度時，近似熵不能反映匯率時間序列真實的波動趨勢。

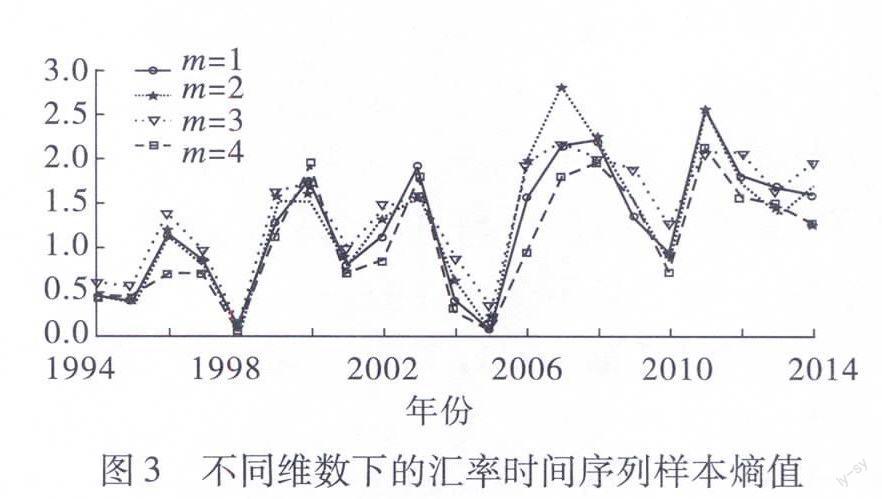
利用matlab得出從1994年到2014年的樣本熵，并畫出了m=1到m=4不同維度下匯率時間序列樣本熵的變化趨勢，結果如圖3所示。通過圖3，我們可以清楚地看出樣本熵值在1998年、2001年、2004年、2009年、2010年都發生了驟降。1996年我國實現人民幣經常項目可兌換，外匯政策進行了重大調整，1997年的東南亞金融危機，2000年的美國新經濟危機，2001年的“9·11”恐怖襲擊事件，2008年的環球金融危機。亞洲金融危機是由于泰國實行浮動匯率制而導致的，并迅速在整個亞洲蔓延，直至1998年年末才逐漸平息，對亞洲許多國家的金融市場造成了很嚴重的打擊，中國也因此而被連累，導致了匯率的不平穩。2008年的環球金融危機是由于美國的次貸危機的發生，雷曼兄弟的破產也是導火索，繼而引發了嚴重的貨幣流動性危機，最終影響了全球經濟的動蕩。從亞洲金融危機的經驗教訓看，許多國家貨幣大幅貶值，非但沒起到刺激當地出口的作用，相反，不僅打擊了本國金融業，也造成通貨膨脹，資產縮水，資金外流，最后釀成全面經濟危機[12]。而當時我國經濟之所以“一枝獨秀”，與人民幣的穩定是分不開的。最近，東南亞一些國家的貨幣再次貶值，結果出口下滑更快。如果此時人民幣貶值，則不可避免地會出現競相貶值的局面，釀成新的危機。

由此可以看出樣本熵在此時可以很好的反映匯率時間序列的波動情況；并且匯率時間序列的樣本熵值在不同維度下并沒有發生太大的變化，說明此時的數據量已經做夠樣本熵算法進行精確的計算了。

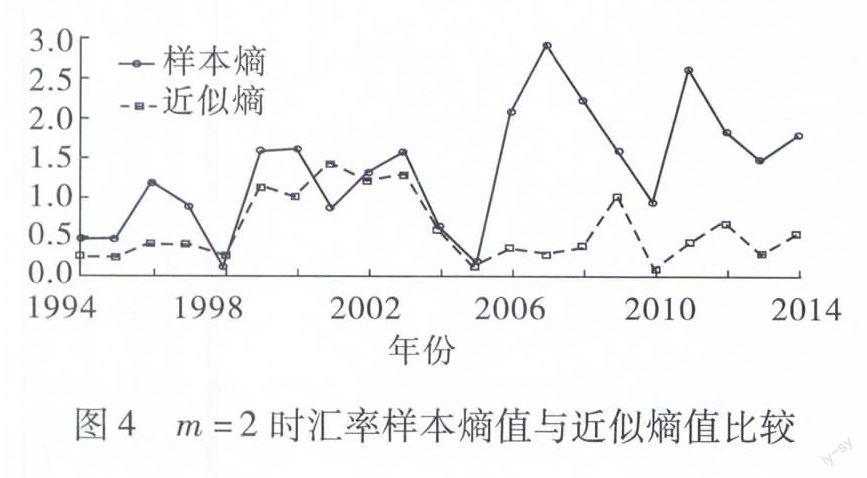
為了更明顯的看出樣本熵值與近似熵值的不同，文章將m=2時的樣本熵值與近似熵值進行對比分析，如圖4所示。我們可以明顯的看出在2001年時，樣本熵值發生了驟降，而近似熵值卻仍然在上升，即此時的近似熵算法沒有反映出2000年的美國新經濟危機、2001年的“9·11”恐怖襲擊事件和2008年的環球金融危機對中國匯率市場的影響；在2008年和2009年時，近似熵值雖然也上升了，但上升幅度很小，說明近似熵的靈敏程度不如樣本熵。并且近似熵數值相對于樣本熵數值較小，熵值越小代表時間序列越簡單，而事實上匯率市場數據變化幅度很大，所以樣本熵比近似熵能更好的反映匯率時間序列的波動情況。

3 結 語

文章將熵估計方法應用于匯率時間序列中，用于識別匯率市場在不同時間的波動狀態并加以分析。在不同維度下討論了近似熵與樣本熵反映匯率時間序列波動的情況，并對同一維度下近似熵與樣本熵效果進行了比較，發現樣本熵比近似熵可以更好的反映匯率的波動性，并且更加靈敏。樣本熵算法在匯率市場中良好的反映了大事件的發生與延續，解決了近似熵算法對微小的復雜性變化不靈敏的缺陷，并且顯著提高了熵估計在短時間序列上的可用性和精確度，并且樣本熵算法可以應用于醫學、金融和多種時間序列數據中，它也可以應用到更短的股票數據中。例如一周或一天不同節點的單只股票中，檢測它是否穩定，如果熵值較高，序列變化無序，不宜進行投資；如果熵值較低，序列平穩有序，可以結合統計上的預測方法，進行投資規劃。該算法的提出為短時間序列的檢測提供了新的思路。

參考文獻：

[1] Ghashghaie S，Breymann W，PeinkeJ，et al.Turbulent cascades inforeign exchangemarkets[J].Nature，1996，381（6 585）：767-770.

[2] Laloux L，Cizeau P，Bouchaud J P，et al.Noise dressing of financial correlation matrices[J].Physical Review Letters，1999，83（7）：1 467-1 470.

[3] 趙麗麗，唐 鎮，楊會杰，等.基于復雜網絡理論的時間序列分析[J].上海理工大學學報，2011（1）：47-52.

[4] 戴瑩星，孫宗國.人民幣匯率的變化及其對中國經濟的影響[J].法制與社會，2008（7）：100-101.

[5] 嚴捷冰，楊會杰.基于擴散熵的平衡估計的兒童行走序列研究[J].上海理工大學學報，2014（2）：147-153.

[6] 苑 娟，萬 焱，褚意新.熵理論及其應用[J].中國西部科技，2011（5）：42-44.

[7] 喬坎坤，盧志明.擴散熵方法對股指內在規律性的分析[J].復旦學報：自然科學版，2013（5）：712-716.

[8] Pincus S，Kalman R E.Irregularity，volatility，risk，and financial market time series[J].Proceedings of the National Academy of Sciences of the United States of America，2004，101（38）：13 709.

[9] Costa M，Goldberger A L，Peng C K.Multi-scale entropy analysis of complex physiologic time series[J].Physical Review Letters，2002，89（6）：068 102-1-4.

[10]Richman J S，Moorman J R.Physiological time-series analysis usingapproximate entropy and sample entropy[J].American Journal of Physiology-Heart and Circulatory Physiology，2000，278（6）：2 039-2 049.

[11]Lake D E，Richman J S，Griffin M P，et al.Sample entropy analysis of neonatal heart rate variability[J].American Journal of Physiology-Heart and Circulatory Physiology，2002，283（3）：789-797.

[12]張灝泉.分析人民幣匯率對我國經濟的影響[J].現代管理科學，2003（1）：76-77.