大學數學中幾何方法的運用
劉昂洋

【摘要】針對大部分大三學生來說,大學數學課程內容難度較大,而且極為重要.大學數學是大部分理工課程的基礎課程,有利于理工科學生之后的學習,對學生具有積極意義.學生在學習過程中如使用幾何方法,能夠有效提高自身學習質量.本文簡要分析了學生在高等數學學習過程中所存在的問題,同時從闡述數學思維、簡化求解過程等多方面分析了學生應如何在大學數學學習過程中應用幾何方法,以期增強學生的邏輯性以及提高學生學習能力.
【關鍵詞】大學數學;幾何方法;實際運用
對理工科學生來說,大學數學是必修課程,其不僅為學生之后專業課程的學習奠定了基礎,同時也培養了學生良好的邏輯思維能力,使其更為適應之后的社會生活.因此,大學數學的學習質量頗為重要.然而,就目前而言,我國大部分學生的學習水平有待提升,學習過程也存在較大的問題.幾何方法可以使學生更為直觀地理解邏輯內容.因此,學生應積極在大學數學學習中運用幾何方法,以提高自身學習質量,同時加深對大學數學知識的理解.
一、大學數學學習中存在的問題
(一)學習時間以及資源不足
大學數學是理工科類學生學習專業課知識的必備工具,如物理中的力學、電學等課程知識的學習都涉及了大學數學中的知識.定積分的幾何運用在機械設計課程中得到廣泛應用.然而,就目前而言,我國大部分大學給予大學數學課程的課時并不多,但該課程知識內容數量繁多,且學習難度較高,學生難以在課堂短時間內消化,所以學習時間明顯不足.加之課堂知識內容被大幅壓縮,將部分定理的證明過程直接刪除,學生單純依靠記憶進行理解與使用,忽視了以幾何的角度理解定理,導致大部分學生并不理解定理的來源,也不理解定理的幾何意義.除此以外,部分高校還需面對教學資源不足這一問題.部分學校的教師或是教室會存在不足的現象.受教學資源的限制,部分高校采取大班授課的方式,令多個班級甚至多個專業同時聽課.如此一來,學生即使在學習狀態、進度以及學習方式等方面出現問題,由于人數眾多,無法直接向教師提問.且課堂氣氛沉悶單調,學生無法與教師或是其他學生進行直接交流與討論.只好被動接受知識,無法進行自主思考以及對知識的創新,課堂學習效率自然難以提升.
(二)學生學習方式存在問題
學生在學習過程中,應注重調節自身心態,注意自身課堂細微的情感變化.學生學習狀態、熱情度以及積極性直接影響了其課堂教學效率.大部分學生學習時,往往只研究課本上的定理及其證明內容,但定理及其證明方面的知識晦澀難懂,且學習過程枯燥無味,導致學習過程較為沉悶無趣,久而久之,學生便會逐漸喪失學習興趣.所以,若學生采用上述學習方式,便限制了自身思維,逐漸喪失了學習熱情,甚至產生厭學的洗能力.學生采用幾何方法學習,能夠使數學知識更為直觀,容易理解.同時也能令學習過程較為輕松.但是部分學生卻過于依賴使用幾何方法進行學習,忽視了對數學思想的解釋,或是直接利用幾何圖像替代了教材中的定理以及相關證明,從而令自身無法更為深入地理解問題,從理性的角度看待以及解決問題.由此可見,部分學生無法正確使用幾何方法,導致學生學習方式存在較大問題.不僅如此,學生若不將代數與幾何聯系為一體,之后的學習也會收到一定影響,以建筑工程為例,建筑工程中大部分問題為幾何問題,而大學數學中大部分為代數語言,若學生僅了解幾何內容,則學生生無法了解兩者之間的聯系.同理,若學生僅了解大學數學中代數內容,則無法利用大學數學知識解決建筑工程中的問題.
(三)學生對幾何方法的認識有誤
隨著現代科技的發展,信息技術在大學學習中的應用逐漸豐富.學生可借助目前的科技設備,如計算機、手機等設備構建更為形象以及直觀的圖形,圖形也由平面圖形轉化為立體圖形,使得學生突破了空間限制,也解決了之前紙筆繪制圖形時,圖形不準確這一問題.然而,學生在構建圖形并進行研究的過程中,往往會走向誤區,發生以偏概全的現象.大部分學生繪圖過程中不理解幾何方法的實質,錯誤地認為,針對定理證明問題,無需使用嚴謹的數學語言以及邏輯進行驗證,只需繪制特定函數的函數圖像即可.然而并非如此,學生運用幾何方法理解定理以及定理證明內容,實質是舉例,但舉例并不能包括所有的狀況,所以學生在學習之前,需反復研究幾何示例,同時清楚、了解幾何學習方式的特殊性.學生也可選用多個幾何示例作為對比,更為深入地了解幾何學習方式的實質.
二、大學數學中幾何方法的實際運用
(一)闡述數學定理
數學定理是課程內容的重點,學生學習數學定理的目的,不僅是要求自身對數學定理有所記憶,還需對知識有一定理解,同時能夠靈活運用.然而,大學數學數學的定理知識過于抽象,大部分學生抽象思維能力不足,難以理解定理內容,對定理所描述的情況也沒有清晰地認識,使得學生雖然能夠記憶定理,但無法深刻理解,也難以正確運用.針對上述情況,學生便可運用幾何學習方式,將定理轉化為圖像,使定理的表現形式更為直觀,也有利于自己接受.
(二)簡化題目
數形結合思想一直是數學常用的思想之一,其不僅能夠令題目變得更為直觀與形象,同時也能簡化題目步驟,從而提高學生的解題效率以及正確率.部分題目如果僅依靠代數進行計算,計算量較大,計算過程中容易發生錯誤.若學生將題目部分量轉化為圖形,則能夠輕易觀察到各量值之間的關系,同時也省去大量計算,大大降低了出錯的概率.
如題:設存在一旋轉拋物面,該拋物面方程為z=x2+y2,同時存在一平面,方程為x+y-2z=2,求解兩面之間相距距離最短時是多少.
該問題共有兩種求解方式:第一種方法,學生可使用條件極值的方式進行求解,單純依靠代數知識解答,其中并不涉及任何幾何方式.該方法具體如下:
在旋轉拋物面上隨意截取一點,設該點坐標為P(x,y,z),那么點P與平面x+y-2z=2之間相距的距離可通過下列式子表示:d=16|x+y-2z-2|.此時,問題便發生了變化,即求解約束條件下,函數f(x,y,z)=(x+y-2z-2)2的極限值.學生設立拉格朗日輔助函數:F(x,y,z,λ)=(x+y-2z-2)2-λ(x2+y2-z).由上可得:
計算完成后,可知拉格朗日函數有且僅有一個駐點,即x=y=14,z=18,λ=1.將上述數值代入算式d=16|x+y-2z-2|當中,此時便能求的旋轉拋物面同平面之間的距離最短時為746.
該解答方法看似步驟較為簡潔,但其計算量極大,且學生在求解駐點時,方法也是極為繁瑣,且會耗費學生大量時間.所以,學生可使用第二種方法,即結合幾何方法進行求解.具體解法如下:
從幾何的角度進行分析,若希望旋轉拋物面z=x2+y2上任意一點同平面之間的為最短距離,那么旋轉拋物面z=x2+y2上點的法向量應當與平面的法向量保持平行關系.在旋轉拋物面z=x2+y2上任取一點,設該點為P,坐標為P(x,y,z).此時可以通過求解得出,點P處,旋轉拋物面的法向量,表示為(2x,2y,-1),還有平面的法向量(1,1,-2).所以可得:2x1=2y1=-1-2.
通過上式可以解出:x=y=14.之后將該結果代入旋轉拋物面方程當中,可解得結果z=18.學生再將所得結果代入求解點與平面距離公式當中,便能夠求得結果d=746.
(三)運用幾何圖像活躍思維
數學定理一定有其形成過程,也有其思考以及證明過程.學生若只是背誦了定理,而不了解其產生的原因以及過程,便無法靈活運用.學生應結合圖像探索定理的實質內容.以極為重要的極限limx→0sinxx=1為例,該極限在之后的使用都較為頻繁.然而學生是無法通過定義以及極限運算的方式了解該極限的含義,需要使用夾逼準則進行證明.然而,以學生的能力,難以找到與sinxx相關的不等式.學生需使用x同正弦函數sinx之間的聯系作為引入,復習高中所學的有關
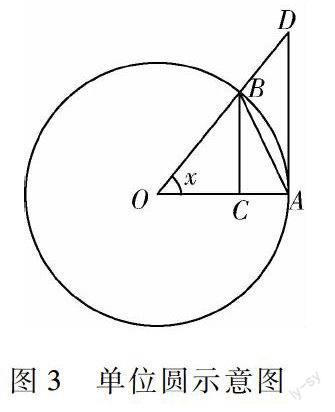
圖3單位圓示意圖三角函數的知識,構建單位圓,尋找x、sinx以及tanx之間的關系.具體如圖3所示,設定∠AOB=x,其中x的取值范圍為0,π2,使得BC與OA為垂直關系.學生可知sinx=2S△AOB,x=2S扇形AOB.之后學生尋找tanx的代表式,構建圓的切線,令圓過點A,且與OB延伸線相交,交點為點D,此時tanx=2S△AOD,通過面積大小的對比,學生較為容易得出sinx結束語
大學數學是理工科學生學習其他專業課程必備的知識,所以對學生之后的學習生活尤為重要.作為學生,應靈活運用幾何學習方式輔助自己進行學習,從而提高自身學習效率,提升數學水平.
【參考文獻】
[1]林冠男,肖歡歡.關于在大學數學教學中加強幾何教學的幾點意見[J].才智,2015,30:213.
[2]王輝.幾何方法在大學數學教學中的應用[J].教書育人(高教論壇),2015,30:88-89.
[3]陳維桓.關于在大學數學教學中加強幾何教學的幾點意見(續)[J].高等數學研究,2013,01:5-6.
[4]賈長虹,范志勇,葉留青.數學分析中的幾何直觀方法[J].焦作師范高等專科學校學報,2012,01:47-49.
[5]李榮祥.幾何方法在數學分析教學中的運用[J].惠陽師專學報(自然科學版),2013,03:36-38.

