另辟蹊徑，挖掘數學錯題中蘊含的教學價值

劉艷

在學習的路上，有成功，也有失敗.在數學學習的前進路途中，正確與錯誤也是并肩同行的.知識能力再強的學生，在解答數學問題時也不可能不出現任何錯誤.既然錯題的出現在所難免，我們便不應當去逃避和畏懼，而是需要轉變思路，化被動為主動，從之前遇到錯題就灰心，轉變為從錯題當中主動挖掘價值，并將之運用到數學學習效果強化的過程當中去.本文就是以此為立足點，站在一個全新的視角上，另辟蹊徑去看待初中數學當中出現的錯題，為教師們的教學提供另一個思路，也為學生們的學習尋找另一個入口.

一、借助知識性錯誤，彌補學習漏洞

在導致錯題出現的眾多錯誤類型當中，知識性錯誤是最為“接地氣兒”的一種，這類錯誤主要是由于學生們對于基本知識內容的理解出現了偏差，或是對題目當中所給出的條件產生了遺漏或誤判而產生的.因此，透過知識性錯誤，教師們常常能夠非常直觀地發現學生目前的知識漏洞，進而有的放矢地對之進行及時的彌補與完善.

例如，在一次分式運算的課堂練習中，一名學生在計算2x+2-2x-2時，出現了一個十分明顯的錯誤，將原式化簡為2（x-2）-2（x+2）=2x-4-2x-4=-8進行計算.表面看來，這個錯誤出現得非常不應該，甚至有些可笑，但我卻抓住了這個錯誤背后的知識性原因：學生混淆了分式運算與解分式方程這兩個內容.于是，我沿著這道錯題的方向，請學生們繼續求解方程2x+2-2x-2=A.如此一來，學生們借助一個看似荒唐的知識性錯誤，再次區分了彼此相近的兩個數學內容，并重新明確了兩種問題的解答方式.

知識性錯誤是一種基礎性錯誤，也是教師和學生絕不可以忽略的錯誤.正如建造大樓需要先打好地基一樣，想要將初中數學學得好、學得透、學得活，最重要的一個前提就是要將基本的概念、公式、定理等內容掌握好，并在解答具體問題時，將已知條件吃透.只有在這個堅實的基礎上，方能繼續調動思維與方法，對數學內容進行深層次探究.

二、借助邏輯性錯誤，強化應變能力

基礎知識掌握得非常扎實，解答基本問題從不丟分，但面對復雜問題時便會手足無措，無從下手，然后出現錯誤——這是很多初中學生在數學解題過程當中所出現的現象.對于這種錯誤，我們將之界定為邏輯性錯誤.也就是說，當這一類錯誤出現時，原因并不在于學生對于基礎知識理解不到位，而是在于數學邏輯不夠清晰，面對復雜問題時，有效處理的能力不強.

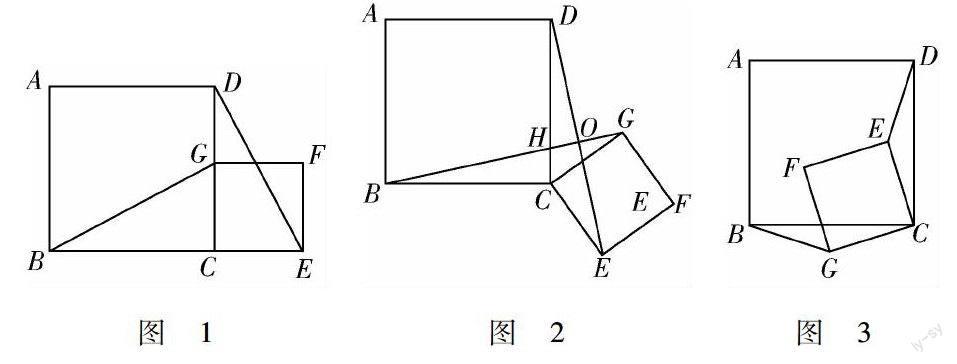
例如，在完成了四邊形內容的教學后，我請學生們解答如下問題：如圖1，四邊形ABCD是正方形，G是CD上的一個動點且不與C、D重合.以CG為邊在ABCD外作正方形CEFG，連接BG、DE，請判斷線段BG與DE的長度關系及所在直線的位置關系.將圖1中的正方形CEFG繞點C旋轉任意角度至圖2、3位置，上述結論是否成立？若將原題中的正方形改為矩形，且AB=a，BC=b，CE=kb（a≠b，k>0），上述結論是否繼續成立？這道題從條件的變化到思維的轉換都是比較復雜的，很多學生手忙腳亂無法解答.經過耐心分析，大家意識到以轉化思想、運動變化思想與動靜結合思想來安排邏輯的重要性，以此為據應對復雜局面，在運動變化中尋求不變.

由此可見，將基礎知識掌握到位了，也并不能保證，學生們可以以之來處理好初中數學當中的所有問題.特別是對于較為復雜的數學問題時，對于學生邏輯能力的要求是很高的.學生們要首先做到不慌張，調動所學知識，快速清晰地整理好思維邏輯予以解答.這才是數學當中所需要的應變能力，也是這類錯題給我們的啟示.

三、借助策略性錯誤，開拓思維路徑

很多時候，作者總會將解答數學問題比喻成一場戰役.因為，如同取得戰役的勝利需要采取正確的戰略戰術一樣，想要完美地解答一個數學問題，也需要選擇一個最優的思維策略.有的學生之所以會出現解題錯誤，并不是知識辨別不足，也沒有邏輯混亂不清，而是由于解題策略選擇不當.

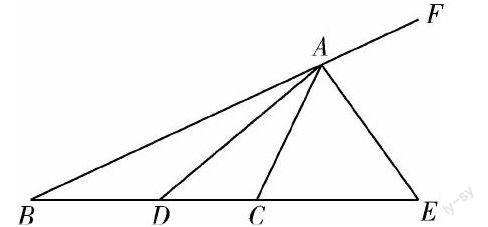
例如，在三角形的習題中，出現過這樣一個問題：如圖，AD和AE分別是△ABC的內、外角平分線，∠ACB-∠B=90°.求證：AD=AE.在思考這個問題時，很多學生非常猶豫，不知道怎樣解才最好.這就是典型的策略性錯誤的表現.一般來講，我們的思維過程是：怎樣證明AD=AE？證明兩邊相等有何方法？哪種方法最好？而若是能夠結合本題所給出的已知條件來思考，便能夠找到具有功能性與特殊性的思維策略：嘗試等角對等邊，并將已知條件轉化為角的關系式進行計算.

解題策略對于數學問題的準確解答來講影響重大.一旦出現策略性錯誤，輕則造成學生在問題思考過程中的時間浪費，舍近求遠，并在這個迂回的同時出現運算錯誤，重則直接導致問題無法求解.策略性錯誤的出現，也為初中師生們敲響了警鐘，這個時期的數學學習，不僅要著眼于具體的知識內容，還應當在必要的時候，站在更高的教學視野上，從方法的高度進行總結，并以之開拓思維路徑，靈活數學解題.

通過上文的論述不難發現，準確挖掘錯題中所蘊含的教學價值之關鍵，在于對錯誤類型進行清晰地區分，進而針對不同類型的錯誤進行分析，對應實現不同的教學深化效果.由于錯題出現在學生初步完成知識學習的基礎之上，因此，這些錯誤往往具有較高的含金量，能夠反映出學生們在當前形成的知識體系當中所存在的薄弱之處.抓住了錯題之中所體現出的知識能力漏洞，也就是找到了下一步深化教學的有效切入點.這種指引作用，就是數學錯題背后最大的價值.