問中求思,思中獲知
張利橙 劉云 崔錦 張應慧

【摘要】數學家哈爾莫斯曾說:“問題是數學的心臟”,問題又是思維的起點,創造的起點.在以學生為主體的理念下,通過導學案呈現出數學教學主線中的關鍵問題,引導學生在思考和解決問題的過程中獲得新知,更加有效地進行數學學習,培養數學能力.
【關鍵詞】二分法;函數零點;學案
學案是學生學習新知識,形成獨立思維的導航圖,是課堂順利,有效進行的方向標.因此,學案的編制至關重要.函數與方程作為高中數學的重要內容,在二者的緊密聯系基礎上,利用二分法求方程的近似解提供了一個新的思路.以下是對普通高中課程標準實驗教科書數學必修1人教A版3.1.2方程的近似解的學案設計.
學習目標:理解二分法的概念,掌握運用二分法求方程近似解的方法;會借助計算器求出給定精確度的方程的近似解;通過用二分法求方程的近似解,感受逐步逼近和二分法的思想,初步形成用函數觀點處理問題的意識.
學習過程:
一、設置情境,提出問題
二、自主探究,獲取新知
2.給定精度ε,用二分法求函數f(x)的零點近似值步驟的記憶口訣:
定,找,中值計算兩邊看;同號去,算,落在異號間;
周而復始怎么辦?上來判斷.
三、合作探究,例題剖析
例借助計算器用二分法求方程2x+3x=7的近似解(精確度0.1).
四、檢驗成果,鞏固提升
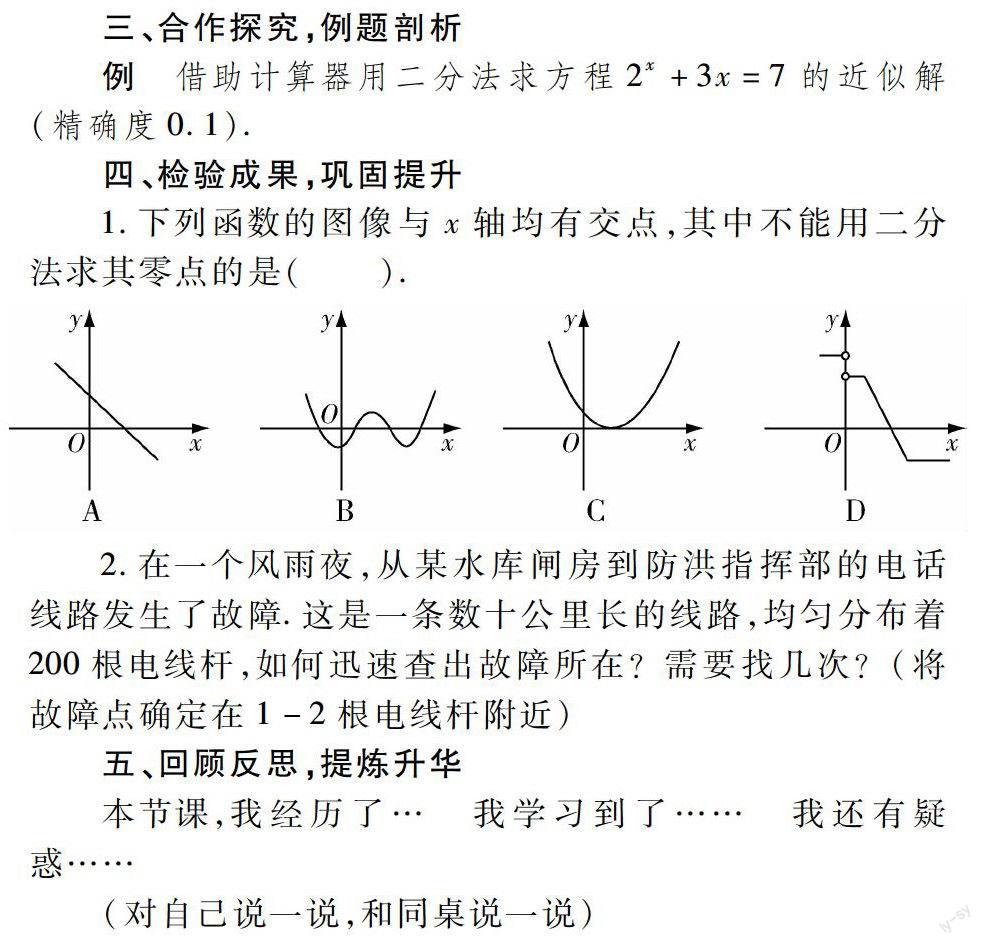
1.下列函數的圖像與x軸均有交點,其中不能用二分法求其零點的是().
2.在一個風雨夜,從某水庫閘房到防洪指揮部的電話線路發生了故障.這是一條數十公里長的線路,均勻分布著200根電線桿,如何迅速查出故障所在?需要找幾次?(將故障點確定在1-2根電線桿附近)
五、回顧反思,提煉升華
本節課,我經歷了…我學習到了……我還有疑惑……
(對自己說一說,和同桌說一說)
六、課后鞏固
(1)借助計算器,求方程0.9x-0.1x=0的實數解個數及其大致所在區間.
(2)閱讀課本P91《中外歷史上的方程求解》,并查閱相關資料,了解二分法的優越性,下節課請同學分享.
設計反思:
數學學習是學生在已有的知識,經驗和理解的基礎上不斷建構數學認知結構的過程.每名學生都有發現問題,提出數學問題、分析問題的能力和創造的潛能,都有一種與身俱來的把自己當成探索者、研究者和發現者的本能,常常具有驗證自己思考結果的欲望.而數學來源于現實,經過對現實的抽象并用符號表示之,再經邏輯演繹和計算而獲得從數學角度對事物性質的認識.本導學案的設計尊重學生的認知規律,通過問題串聯以及競猜書價的活動體會帶領學生二分法在數學中和生活中運用的優越性.通過導學案引導學生參與問題的探究以及問題解決的思維過程,充分調動學生的手、耳、腦、眼,幫助學生積累數學抽象的基本活動經驗,在體驗和感受中實現數學情感升華.
【參考文獻】
[1]董倩英.數學課堂有效提問的策略研究[D].天津:天津師范大學學位論文,2011.
[2]孔凡哲,曾崢.數學學習心理學[M].北京:北京大學出版社,2012(2):2.
[3]章建躍,朱文芳.中學數學教學心理學[M].北京:北京教育出版社,2001:40.

