大規模風電并網條件下AGC機組跨區分布式最優協調控制

張　磊　羅　毅　肖雅元　葉　婧　王　罡

(1.華中科技大學電氣與電子工程學院　武漢　430074 2.武漢大學電氣工程學院　武漢　430074 3.國網天津市電力公司經濟技術研究院　天津　300000)

?

大規模風電并網條件下AGC機組跨區分布式最優協調控制

張磊1羅毅1肖雅元1葉婧2王罡3

(1.華中科技大學電氣與電子工程學院武漢430074 2.武漢大學電氣工程學院武漢430074 3.國網天津市電力公司經濟技術研究院天津300000)

摘要我國風電資源主要集中在西部和北部，外送是解決風電消納問題的有效手段。但隨著風電滲透率的增加，其不確定性帶來的風電功率波動造成部分區域或省份的自動發電控制(AGC)出現了較為嚴重的調節資源不足及控制問題。為解決這一問題，利用分布在全網的AGC機組實現跨區分布式最優協調控制。引入協調因子建立AGC最優協調控制模型，采用原始對偶梯度算法對該模型進行變換，并利用線性變換得到基于協調因子的分布式最優協調控制器。仿真算例表明，隨著風電滲透率增加，各區AGC機組能協調地進行頻率控制，有效平衡風電不確定性引起的功率不平衡量。

關鍵詞：分布式最優協調控制大規模風電并網自動發電控制頻率控制

0引言

我國風電資源主要集中在西部和北部。將西部和北部的大規模風電采用特高壓或超高壓交流或直流輸送到負荷集中的中部、東部和南部地區是我國能源利用的趨勢。由于風電功率存在固有的波動特性[1]，大規模風電并網后需要有相應的調節電源平抑風電功率波動，以確保電網頻率在允許范圍內。按照我國目前各省采用聯絡線功率頻率偏差控制(TBC)方式來分省平衡省內功率缺額的方法，風電滲透率越高的省份所需的調節容量越大，部分區域或省份必然會出現嚴重的調節能力不足問題。根據我國調節資源分布情況，有一些調節能力不足區域或省份不具備建設調節電源的條件，或建設調節電源非常不經濟。而一些區域或省份(如西南地區)則可建設大容量的調節電源。可見，大規模風電并網后若僅采用省調自動發電控制(Automatic Generation Control，AGC)機組分省平衡方式進行調節將失去意義，研究大規模風電并網后如何實現頻率調整是一個全新的課題。

目前國內外學者進行了一些相關的研究工作。文獻[2-5]利用儲能資源快速響應的特點，提出了采用儲能資源參與AGC調頻的各種控制策略。但該方法需要建設儲能裝置，僅能應用于風電滲透率較小的情況，且儲能裝置還需面臨頻繁調節的問題。文獻[6]研究了高風電滲透背景下高峰時段面臨的問題，提出了非AGC機組與AGC機組高峰協調控制策略。文獻[7]采用分布式增量一致算法，構建了分鐘級時間尺度下的風電場與AGC機組分布式協同實時控制模型。文獻[8]利用最優控制實現了負荷側對一次調頻的控制。以上文獻考慮在引入新的頻率調節資源(儲能、非AGC、風電、負荷側)以期彌補省內調節資源不足的情況。另一方面，部分學者利用全網發電資源(包括非AGC機組、AGC機組以及負荷側)和超短期風電功率預測值，通過經濟調度[9，10]調節發電機組的基點功率來抑制風電功率波動。文獻[11]采用鞍點設計法(SDA)實現實時的經濟調度，本質上是從經濟調度的角度對發電機組(包括AGC機組)的基點功率進行實時調節來實現頻率控制。但是在實時調度時間尺度上調節任務主要是由AGC機組來承擔，實時經濟調度僅能提高和優化AGC機組的調節能力。利用全網發電資源通過經濟調度來抑制風電功率波動不能從根本上解決本文提出的調節能力不足帶來的問題。

可見，在風電大規模外送時，AGC作為智能電網調度控制系統的必備手段之一[12]，應通過調整面向常規機組的控制模式和分省平衡控制方式來滿足新能源接入后實時控制的需要，改進原有區域控制思想，在更廣泛區域范圍內進行協調控制，解決風電功率波動對電網帶來的影響。

本文考慮區域或省間調節容量的相互支援，引入協調因子來構建基于全網AGC機組的最優協調控制數學模型。采用對偶思想及線性變換方法對最優協調控制模型進行轉換，結合現有電網AGC控制動態方程獲得了基于協調因子的分布式最優協調控制器。并通過三區域仿真模型，對本文提出的分布式最優協調控制進行了驗證。同時采用某地區2013年典型時段凈負荷波動(負荷波動與風電功率波動的差值)數據進行仿真，結果表明在風電高滲透率條件下，相比于傳統AGC控制，本文采用分布式最優協調控制能有效地應對風電不確定性帶來的功率波動造成的影響。

1全網AGC機組最優協調控制數學模型

風電外送過程中需對外送電量及備用決策進行一定調整[13]。外送通道不僅要外送電量還需承擔送端地區的備用需求，該備用需求為AGC機組跨區協調控制提供了先決條件。如圖1所示，本文采用全網AGC機組來跨區平衡風電波動。

圖1　全網AGC機組跨區協調控制原理圖Fig.1　The schematic of AGC unit trans-regional coordination control

當A區大規模風電波動時，傳統AGC控制模式僅由A區的AGC機組參與。

為了利用全網AGC機組同時協調參與控制以平衡風電波動，需要構建全網AGC機組協調控制模型。為此，首先分析在面對風電波動時各區AGC機組的動態控制過程及其穩態特性。研究AGC控制時通常采用平均系統頻率模型(ASF)[14]，在互聯系統中該模型主要包括以下幾個動態環節。

1)發電機負荷動態方程[15]

(1)

(2)

2)聯絡線動態方程[15]

(3)

3)原動機及調速器動態方程

為簡化分析，本文采用一階慣性環節來表征原動機和調速器特性[16]，如式(4)所示。

(4)

4)AGC控制動態方程[16]

以常用的積分環節AGC控制為例，可得

(5)

式(1)～式(5)為進行AGC控制的動態方程，采用ASF模型進行分省模式下的仿真可得各變量的穩態解。

Ν區域

(6)

Ω區域

(7)

式(7)表明，在分省協調控制模式下風電受端區域無法參與風電功率波動控制。

文獻[17]提出的協調因子表示省內各AGC機組參與二次調頻的份額。本文提出廣域協調因子(簡稱協調因子γ)的概念，表征各區參與全網協調控制的份額，并構造了全網AGC機組跨區最優協調控制數學模型為

(8)

(9)

(10)

(11)

(12)

2基于協調因子的分布式最優協調控制器

2.1基于對偶思想的最優控制分析

為實現式(8)～式(12)所示模型的控制，由文獻[16]，本文從該最優問題的對偶問題入手構造基于協調因子的最優控制器。引入拉格朗日乘子λi∈RΝ×1、 λj∈RΩ×1、 μi∈RΝ×1、 μj∈RΩ×1。

式(8)～式(12)可改寫為

(13)

式中，i∈Ν； j∈Ω。

對式(13)采用原始對偶梯度算法[16]可得

Δfi=λi

(14)

式中，i∈Ν∪Ω。

(15)

式中，i, j∈Ν∪Ω。

(16)

式中，i, j∈Ν∪Ω。

(17)

式中，j∈Ν∪Ω。

(18)

式中，i∈Ν。

(19)

式中，j∈Ω。

(20)

式中，i∈Ν。

(21)

式中，j∈Ω。

εγij、 εPij、 εPj、 ελi、 ελj、 εμi、 εμj均為正的步長。對比式(17)～式(21)和式(1)～式(5)，原始對偶梯度算法的對偶變量與頻率控制中的狀態變量有較為密切的聯系，因此，對變量進行線性變換(λ, μ)→(Δf,ΔPC)，可得如式(22)所示關系。

(22)

將式(22)帶入式(14)～式(21)求解可得

(23)

令

(24)

將式(14)及式(22)～式(24)帶入式(15)～式(21)可得

(25)

式中，i∈Ν。

(26)

式中，j∈Ω。

(27)

式中，i, j∈Ν∪Ω。

(28)

式中，j∈Ν∪Ω。

(29)

式中，i∈Ν。

(30)

式中，j∈Ω。

(31)

式中，i, j∈Ν∪Ω。

式(25)～式(28)與傳統AGC控制的動態方程式(1)～式(4)一致。求解式(25)～式(31)可得式(8)～式(12)的最優解。即根據式(29)～式(31)可實現基于協調因子的AGC機組跨區最優協調控制。

2.2分布式最優協調控制器實現

(32)

圖2　AGC機組跨區分布式最優協調控制器Fig.2　AGC unit’s trans-regional and distributed optimal coordination controller

式中，εμi、 εμj為式(23)所示的常系數；εγij為決策因子，網調中心可根據電力系統運行的實際情況通過決策因子調節各區AGC機組的參與度。由式(32)可知協調因子Δγ僅需本控制區域的實時信息即可計算獲得。綜上，本文采用式(29)、式(30)和式(32)構造了基于最優協調特性的三區域分布式控制器。如圖2所示，各區計算本區的協調因子后，互相通信實現協調因子的互相交換。從物理角度，各區協調因子攜帶的是基于本區控制能力的功率可調節量信息，協調因子間相互通信實現各區調節量的相互協調和平衡。從控制角度，各區在協調因子的作用下實時修正ACE實現風電不平衡功率在全網中的協調分配，協調因子攜帶的是各區在平衡風電功率波動中的協調調節量信息。

3算例分析

在Matlab/Simulink中構建如圖1所示的三區域互聯電力系統作為測試算例，并采用圖2所示設計跨區分布式最優協調控制器。該互聯系統總的最大負荷為5 200 MW，常規裝機4 500 MW。各區由3條聯絡線連接，其聯絡線電抗分別為xAB=0.059 6 (pu)、xAC=0.038 6 (pu)、xBC=0.029 4 (pu)，網調AGC機組參數及系統各區情況如附表1和附表2所示。假設A區風電基地滿發出力的概率很小，全年風電出力超過風電銘牌容量64%的概率不足5%。在本仿真系統中考慮傳輸通道對風電消納的促進作用，風場出力按照銘牌出力的75%考慮。此外預留20%的聯絡線備用需求。風電出力具有典型的反調峰特性，因此，風電出力占總體負荷的比重在28%～72%，風電預測誤差設為20%。

3.1不同風電滲透率下的分布式最優協調控制

現考慮決策因子為1，風電滲透率在28%、50%及72%三種方案下的分布式最優協調控制，其風電波動量分別為276 MW、332 MW、479 MW。采用階躍響應作為風電波動輸入，其不同方案下的頻率偏差對比如圖3所示。在傳統AGC分省控制模式下，由于風電所在區域調節量不足，隨著風電滲透率的增加，頻率偏差越來越大。在AGC分布式最優協調控制下，即使風電滲透率增加到72%也能很好地保持頻率穩定。

圖3　不同風電滲透率下頻率偏差Fig.3　Frequency deviation in different wind power penetration

圖4為不同風電滲透率下各區協調因子變化情況。風電所在區域的協調因子與風電受端協調因子具有相反的變化趨勢且各時刻協調因子之和為零。

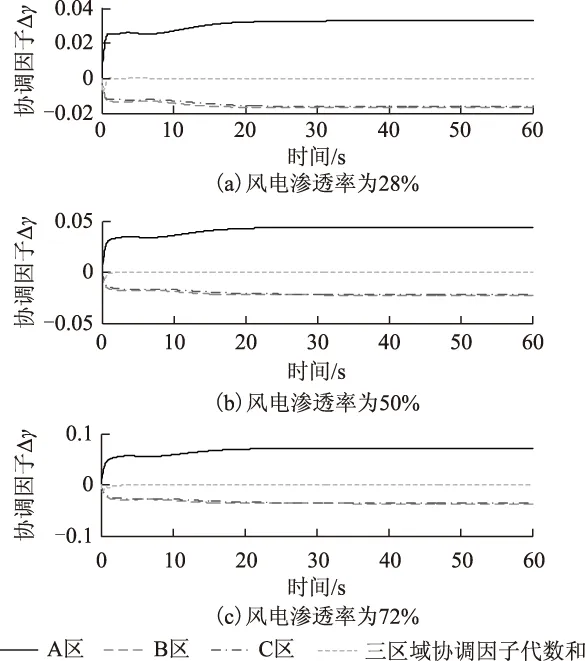
圖4　不同風電滲透率下各區域協調因子變化Fig.4　All regions coordination factor in different wind power penetration

圖5為各區AGC機組出力變化情況。A區AGC機組在不同風電滲透率下都已達到極限出力變化；若按傳統方法進行控制，此時風電所在區域無法調節該風電波動下的功率不平衡。但采用協調控制后，B區和C區協調參與了A區風電功率的波動控制，使得風電功率波動在全網范圍內得到了有效調節，對互聯電網的頻率穩定起到了重要的支撐作用。

圖5　不同風滲透率下各區域AGC機組出力Fig.5　All regions AGC output in different wind power penetration

3.2不同決策變量下的出力費用對比

表1為不同風電滲透率下各區AGC機組的出力及調節費用。在不同風電滲透率下A區的出力和調節費用不變，B區和C區的調節費用隨著滲透率的增加而增大。但隨著風電滲透率增加，B區和C區調節費用的比值一直穩定在0.86左右，沒有隨風電滲透率的增加而發生劇烈變化。

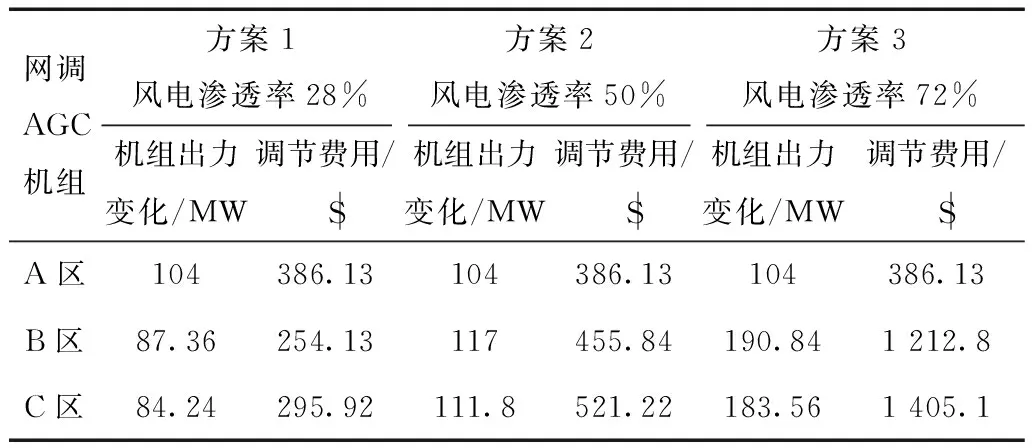
表1　不同方案的機組出力變化及調節費用

圖6為風電滲透率在50%時，不同決策因子條件下B區和C區調節費用的比值。

圖6　不同決策因子調節下B、C區調節費用比值Fig.6　B and C adjustment cost ratio in different decision factor

由圖6可知，隨著決策因子的增加，B區和C區的調節費用比值在不斷增加。以上分析表明，決策因子具有調節各風電受端區域調節費用的作用，網調中心可利用該特性合理調節決策因子，更經濟地確定各協調區域AGC機組的頻率調節出力。

3.3某地區典型凈負荷波動下的分布式最優協調控制

為驗證本文所提控制器在實際中的控制能力，選取某地區2013年某時段10 min凈負荷波動數據作為波動源，如圖7所示。

采用本文所提協調控制可得頻率偏差情況，如圖8所示。與傳統AGC控制方法相比，在風電功率波動期間，采用分布式協調控制的系統頻率偏差一直在0附近波動，且波動范圍一直保持在允許范圍之內。傳統AGC控制的頻率一直在-0.004 (pu)附近波動。即在傳統控制模式下無法提供充足的調節量來平衡風電功率波動，使得頻率偏差超出允許的范圍，給電網安全穩定運行帶來了較為嚴重的影響。

圖7　某地區某時段凈負荷波動Fig.7　A period of net load fluctuations in a region

圖8　不同控制方式下頻率偏差Fig.8　Frequency deviation in different control modes

圖9為本文所提控制方式下凈負荷波動時各區AGC機組出力變化。圖10為本文所提控制方式下負荷波動時各區域AGC機組出力變化。

圖9　凈負荷波動下各區域AGC機組出力Fig.9　All regions AGC output in net load fluctuation

圖10　負荷波動下各區域AGC機組出力Fig.10　All regions AGC output in load fluctuations

由圖9可知，在協調過程中協調因子優先協調風電波動區域AGC機組出力來調節風電波動，當風電波動區域出力達到極限時，協調因子加大協調區域的AGC機組出力。由圖10可知，風電所在區域負荷波動時，僅由本區域調節，協調因子的作用較小。協調因子所表現出的這種特性使分布式最優協調控制既能滿足傳統AGC控制下的頻率控制，又能在風電發生大規模波動時協調全網AGC機組進行跨區調節，具有較好的工程應用前景。

4結論

本文從跨區協調控制的角度，利用全網AGC機組，引入協調因子實現了基于網調AGC機組的分布式最優協調控制。采用仿真程序及實際波動數據對本文所提方法進行了驗證，所得結論如下：

1)提出了廣域協調因子的概念及利用全網范圍內AGC機組實現跨區協調抑制風電功率波動的思想。

2)設計了一種可以實現跨區協調的分布式最優協調控制器。在更廣范圍內研究了大規模風電并網情況下的AGC控制難題。

3)該分布式最優協調控制即能兼顧現有AGC控制模式，又能協調全網資源進行風電波動抑制。

4)本文未對省內AGC機組間的功率分配問題進行討論，也未對網調AGC機組和省調AGC機組在波動情況下的協調配合問題進行討論。這將是跨區協調控制實際運用過程中需要深入研究的問題。

附　　錄

附表2　系統容量

參考文獻

[1]薛禹勝，雷興，薛峰，等.關于風電不確定性對電力系統影響的評述[J].中國電機工程學報，2014，34(29)：5029-5040.

Xue Yusheng，Lei Xing，Xue Feng，et al.A review on impacts of wind power uncertainties on power systems[J].Proceedings of the CSEE，2014，34(29)：5029-5040.

[2]吳云亮，孫元章，徐箭，等.基于多變量廣義預測理論的互聯電力系統負荷-頻率協調控制體系[J].電工技術學報，2012，27(9)：101-107.

Wu Yunliang，Sun Yuanzhang，Xu Jian，et al.Coordinated load-frequency control system in interconnected power system based on multivariable generalized predictive control theory[J].Transactions of China Electrotechnical Society，2012，27(9)：101-107.

[3]蔡國偉，孔令國，潘超，等.風光儲聯合發電系統的建模及并網控制策略[J].電工技術學報，2013，28(9)：196-204.

Cai Guowei，Kong Lingguo，Pan Chao，et al.System modeling of wind-PV-ES hybrid power system and its control strategy for grid-connected[J].Transactions of China Electrotechnical Society，2013，28(9)：196-204.

[4]彭思敏，竇真蘭，凌志斌，等.并聯型儲能系統孤網運行協調控制策略[J].電工技術學報，2013，28(5)：128-134.

Peng Simin，Dou Zhenlan，Ling Zhibin，et al.Cooperative control for parallel-connected battery energy storage system of islanded power system[J].Transactions of China Electrotechnical Society，2013，28(5)：128-134.

[5]胡澤春，謝旭，張放，等.含儲能資源參與的自動發電控制策略研究[J].中國電機工程學報，2014，34(29)：5080-5087.

Hu Zechun，Xie Xu，Zhang Fang，et al.Research on automatic generation control strategy incorporating energy storage resources[J].Proceedings of the CSEE，2014，34(29)：5080-5087.

[6]王松巖，于繼來.含大規模風電系統的非AGC與AGC機組高峰協調控制策略[J].中國電機工程學報，2013，33(7)：156-163.

Wang Songyan，Yu Jilai.Coordinated dispatch regulation strategy between non-AGC units and AGC units with high wind power penetration[J].Proceedings of the CSEE，2013，33(7)：156-163.

[7]何成明，王洪濤，韋仲康，等.風電場與 AGC 機組分布式協同實時控制[J].中國電機工程學報，2015，35(2)：302-309.

He Chengming，Wang Hongtao，Wei Zhongkang，et al.Distributed coordinated real-time control of wind farm and AGC units[J].Proceedings of the CSEE，2015，35(2)：302-309.

[8]Zhao C，Topcu U，Li N，et al.Design and stability of load-side primary frequency control in power systems[J].IEEE Transactions on Automatic Control，2014，59(5)： 1177-1189.

[9]Mudumbai R，Dasgupta S，Cho B B.Distributed control for optimal economic dispatch of a network of heterogeneous power generators[J].IEEE Transactions on Power Systems，2012，27(4)：1750-1760.

[10]Zhao C，Mallada E，Drfler F.Distributed frequency control for stability and economic dispatch in power networks[C]//American Control Conference，Chicago，IL，2015：2359-2364.

[11]Zhang X，Li N，Papachristodoulou A.Achieving real-time economic dispatch in power networks via a saddle point design approach[C]//2015 IEEE Power & Energy Society General Meeting，Denver，CO，2015：1-5.

[12]滕賢亮，高宗和，朱斌，等.智能電網調度控制系統 AGC 需求分析及關鍵技術[J].電力系統自動化，2015，39(1)：81-87.

Teng Xianliang，Gao Zonghe，Zhu Bin，et al.Requirements analysis and key technologies for automatic generation control for smart grid dispatching and control systems[J].Automation of Electric Power Systems，2015，39(1)：81-87.

[13]焦春亭，管曉宏，吳江，等.考慮大規模風電跨區消納的電力系統調度[C]//第三十三屆中國控制會議，南京，2014：7549-7554.

[14]Chan M L，Dunlop R D，Schweppe F.Dynamic equivalents for average system frequency behavior following major distribances[J].IEEE Transactions on Power Apparatus and Systems，1972，PAS-91(4)：1637-1642.

[15]Kundur P.Power system stability and control[M].New York：McGraw-hill，1994.

[16]Li N，Chen L，Zhao C，et al.Connecting automatic generation control and economic dispatch from an optimization view[C]//American Control Conference (ACC)，2014：735-740.

[17]Bevrani H.Robust power system frequency control[M].New York：Springer，2009.

[18]Andreasson M，Dimarogonas D V，Johansson K H，et al.Distributed vs.centralized power systems frequency control[C]//European Control Conference (ECC)，Zurich，2013：3524-3529.

作者簡介

張磊男，1986年生，博士研究生，研究方向為電力系統優化運行與控制等。

E-mail：104602084@qq.com

羅毅男，1966年生，副教授，研究方向為電力系統優化運行與控制、電力系統安全運行監控和配電自動化等。

E-mail：luoyee2007@163.com(通信作者)

Trans-Regional and Distributed Optimal Coordination Control of AGC Units Under Large-Scale Wind Power Grid

Zhang Lei1Luo Yi1Xiao Yayuan1Ye Jing2Wang Gang3

(1.School of Electrical and Electronic EngineeringHuazhong University of Science and Technology Wuhan430074China 2.School of Electrical EngineeringWuhan UniversityWuhan430074China 3.State Grid Tianjin Power Economics Research InstituteTianjin300000China)

AbstractWind power resources in China are mainly concentrated in the west and north.Large-scale wind power delivery is an effective way to solve the problem of wind power consumption.But with the increase of wind power penetration，the uncertainty caused by the power fluctuation enables that the automatic generation control (AGC) under some regions or provinces appears more serious problems，e.g.insufficient adjustable resources and control.To solve the problem，this paper uses the AGC units distributed in the whole network to achieve the optimal coordinated and distributed control.First，this paper introduces the concept of the coordination factor to establish the optimal coordinated AGC control model.Second，by using the original dual gradient algorithm to transform the model and the linear transformation method，the optimal coordination controller based on a distributed coordination factor is constructed.The simulation examples show that the grid dispatching AGC units can control the frequency deviation in coordination with the increase of the wind power penetration and effectively balance the amount of power imbalance caused by wind uncertainty.

Keywords：Distributed optimal coordinated control，large-scale wind power，automatic generation control，frequency control

中圖分類號：TM734

收稿日期2015-04-09改稿日期2015-06-07