如何開展數學課堂的變式教學
胡連生
摘 要: 教學質量的高低,關鍵在課堂.對于九年級數學教學而言,課堂教學效率直接影響中考數學的成績.在課堂教學中,我們該如何開展教學活動呢?本文將通過一個片段,從“變式教學”這一角度,具體說明“變式教學”的優勢,以及如何開展“變式教學”.
關鍵詞: 數學 變式 相似 折疊
例題:如圖①,在矩形紙片ABCD中,AB=6,BC=8.將矩形紙片沿BD折疊,點A落在點E處,設DE與BC相交于點F,求BF的長.
點評:該題考察了幾何三大變換之一“折疊問題”,涉及了等腰三角形、勾股定理等知識點.
變式:若去掉條件中“AB=6,BC=8”,并將問題改為:
(1)如圖②,連接EC,證明:△BCE≌△DEC.
分析:由上題可知,AD=BC=DE,AB=BE=CD,EC=CE,
所以△BCE≌△DEC.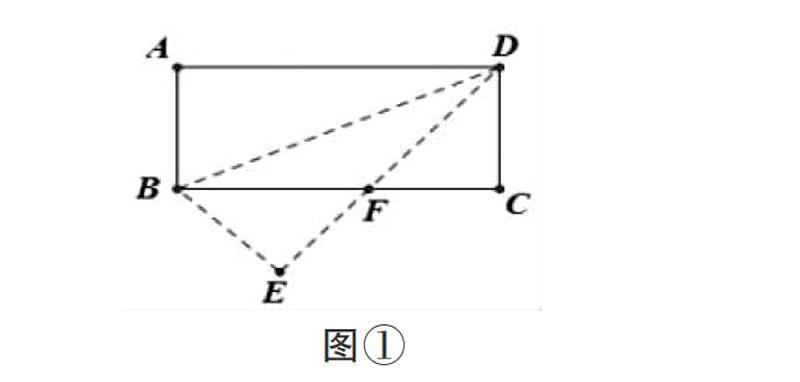
點評:考察了折疊的相關特性,以及全等的判定.
點評:對于這一問的解答,是基于上面幾個小問題的基礎之上提出的,層層遞進,符合學生的認知規律,方便學生總結解題思路和方法.
(4)如圖③,若AB=a(a為不為零常數),點P為BD上一點,過點P作PG⊥BC,PH⊥DE,垂足分別為G、H,求PG+PH.
分析:由題意得,∠ADB=∠BDE,
延長GP,交AD于K點,則PK⊥AD,
所以PK=PH,即PG+PH=PK+PH=a.
點評:在原題的基礎上,考察了角平分線的性質.
通過本文我們可以發現,合理運用“變式教學”,可以增大課堂容量,加強知識點之間的內在聯系,發散思維,提高學生綜合運用的能力.在這個片段中,我們容易發現,在“變式教學”中一定要注重盡可能地以原題為“母版”,變式的題目要注意梯度,層層遞進,切不可難度參差不齊.同時,還要注重變式題之間的銜接是否合理,知識點的運用是否到位,等等.相信如果在平時的課堂教學中,能夠做到以上幾點,再輔以一題多解,那么我們有理由相信,學生會發自內心地喜歡上數學,喜歡學數學.

