預設應然，道理釋然

陳六一　柯曉莉

筆者聆聽了某市優質課評比活動中的10節數學課，都暴露著一個同樣的教學尷尬問題：在相同教學內容的處理中，教師們自認為應是水到渠成的預設，學生卻不領情，始終走不進教案。為什么會出現如此的窘境？是學生的問題嗎？我們該怎樣反思與重構自己的課堂教學？

一、望：教學再現

【案例1】9加幾

教師出示問題：盒子里有9個蘋果，盒子外有4個蘋果。提問：一共有多少個蘋果？學生回答：9+4=13。教師追問：你是怎樣算出9+4等于13的？

生1：用腦袋算的。（聽課教師和學生都笑了。）

師：能說說你是怎樣用腦袋算的嗎？

生1：用腦袋使勁算的。（聽課教師和學生笑得更歡了。）

師：有不一樣的算法嗎？

生2：9+4，就是往9的后面數4個，10、11、12、13。

師：還有不一樣的想法嗎？

生3：9+1=10，4-1=3，10+3=13。

生4：我用小棒代替蘋果，先數9根，再數4根，一起數就是13根。

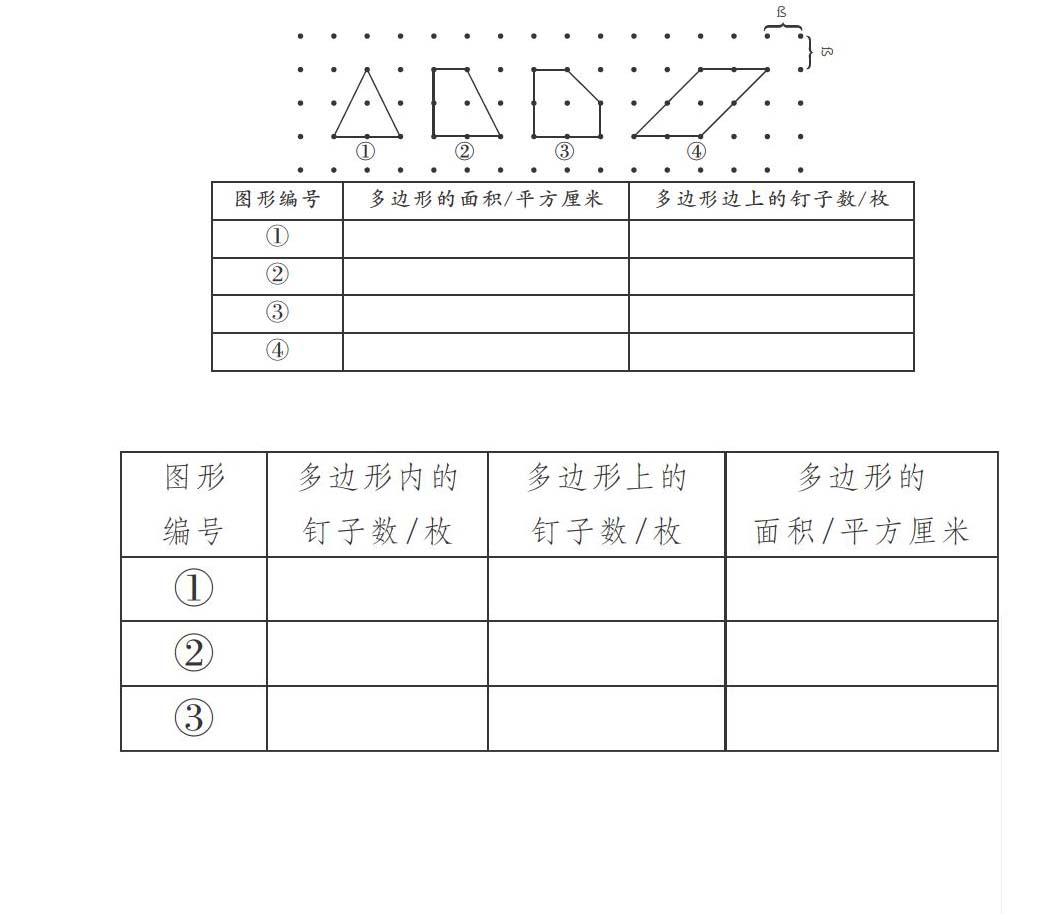
【案例2】釘子板上的多邊形

當學生完成上圖任務后，教師問：你們發現了什么樣的規律？學生異口同聲：多邊形的面積=多邊形邊上的釘子數÷2。教師引導小結：當a=1時，S=n÷2。接著出示內部釘子數為2枚的圖形，并完成如下表格。

學生填寫完畢，教師再次提問：你們發現了什么樣的規律？

生：當a=2時，S=n÷2+a-1。（教師有點意外，頓時不知所措。）

二、問：教師答疑

縱觀以上兩個教學片段，教師預設目標非常明確，“9加幾”希望學生能說出“湊十法”，“釘子板上的多邊形”則期望學生能看出“S=n÷2+1”的規律，可事與愿違。于是，賽課結束，筆者問道：憑什么認為你的預設一定生成？

教師的答案有這幾種：第一，這是教材內容的呈現方式，同時也是教學目標。第二，自己回答這些問題，感覺“湊十法”和“S=n÷2+1”是最佳答案。而且教低段學生的教師指出，在新授課之前，有計算比賽，學生算8加幾、7加幾比算10加幾要慢，那么10加幾的快捷應該會在新知識的學習中有所遷移；教高段學生的教師也表示，當多邊形內部為一枚釘子時，學生能一起發現S=n÷2的規律，那么當多邊形內部為兩枚釘子時，面積S= n÷2+1是最容易遷移的規律，學生不應該舍近求遠。

教師們似乎有理有據，但案例中的教學目標畢竟沒有達成。原來，課堂教學的藝術孕育于教學的科學，學生沒有走進教師的預設，一定有一個為什么。

三、聞：應然診斷

1.簡單計算是語言的提取。 教育心理學發現：20以內的加減法計算通常是語言的提取。也就是說，算9加幾的結果，學生無需用上邏輯推理，而是技能自動化之后的語言記憶。所以“案例1”中教師問學生：“你是怎樣算出9+4的？”學生回答“用腦袋算的”是真切的體現。至于生2和生4是被教師逼問，才有了解題的下策；盡管生3的回答最能體現“十進制”的優越性，且符合“多位數加減法其實是計數單位個數相加減”的本質，可是不屬于先湊十再相加的既定套路，所以課堂中也就被“還有不一樣的想法嗎”和“請下一個同學回答”一筆帶過了。教學尾聲，教師們一般都會讓學生觀察“9+2、9+3、9+4……9+9”中個位數字與算式中后一個加數的規律，以幫助學生快速得出答案，其實也是為了實現脫口而出的計算效果。只是，在教學的起始階段，學生已經脫口而出了，教師卻不做肯定，還讓學生被動經歷一個操作、觀察、語言表達以及計算湊十的過程，再要求學生達到課堂開始的脫口而出，學生反而已被一個個“你是怎么想的”弄糊涂了。

2.缺乏圖形支架容易滋生多種表象圖式。“案例2”中學生沒有得出教師認為的最容易的規律S=n÷2+1，其實都是數據惹的禍。由于缺乏動態圖形的直觀幫助，學生不易發現面積變化的本質：由于內部釘子數的增加，帶來了面積的改變。這樣只觀察靜態表格中“2、5、3.5”“ 2、6、4”“ 2、9、5.5”，學生自然會想到要把每組數據中的三個數字都要用上，所以就有了S=（n+a）÷2的結論。當然，用“下一個”“再下一個”的方式，也一定會有學生說出S=n÷2+1。不過，當有學生答出S=n÷2+a-1時，說明這個學生已經建構了“當a=2時，S=n÷2+1”的模型，甚至類比出了當a=3時，S=n÷2+2；當a=4時，S=n÷2+3……從而抽象概括出了面積S的通項公式。顯然，學生已經走得很遠了，而我們的教學還停留在上一個階段。

四、切：重構釋然

1.怎樣教基于怎樣學

【重構1：9加幾】

師：我怎么覺得9+4=12，是我算錯了，還是你們錯了？

生1：老師，你看，9+4，就是往9的后面數4個，10、11、12、13。

師：看來是我算錯了，我最近老是算錯，誰有什么辦法幫幫我呀？

生2：把9看作10，然后把4少看1個，10+3你肯定不會算錯的。

師：怎么10+3就不會錯了？

生3： 10加幾就是十幾呀。

生4：9+1=10，4-1=3，10+3=13。

師：生2和生4都是想老師把9加4變成……

生5：10+3。

師：那我得到一個啟發，是不是可以將9+5變成……

生6：10+4。

師：9+6？

生7：10+5。

師：哪來的10呀？

生8：從4、5、6里分一個給9就是10呀。

教師知道學生會算9+4=13，但是故意出錯，誘導學生幫助教師改錯，這樣數數、擺小棒便不是案例1中無趣的動手，而是數學證明。“誰有什么辦法幫幫教師呀”不是語言提醒就能實現的任務，需要一定的道理，“湊十”的預設也就得以實現。也許你覺得原本的教學片段和重構中的教學片段學生有相近的回答。不錯！可是，一個是被動，一個是主動，一個操作是無奈的，一個操作是展示智慧的平臺；更重要的，看似學生在幫助老師，其實是在無痕地給反應慢的、沒有很好方法的學生一些示范；那些速度快的同學在教師“哪來的10呀”的問話中再做深層次的思考，這樣“不同的學生在數學上得到不同的發展”。

2.合情推理基于演繹推理

【重構2：釘子板上的多邊形】

師：我們把剛才研究的三角形再請回來。

生：三角形邊上的釘子數沒有增加，但是面積變大了，面積大了1平方厘米。

師：面積增加的地方在哪里？怎么就知道是1平方厘米？

生：面積增加在兩個“翅膀”上，由于內部釘子數增加了1，那么“翅膀” 上的兩個三角形底是1，高也是1，增加的面積就是（1×1÷2）×2=1平方厘米。

師：原來的面積可用S=n÷2+a-1表示，那現在的面積呢？

生：當a=2時，S=n÷2+1。

因為歸納推理是從特例出發，所以往往引發多種邏輯取向；如果在歸納的時候，輔以簡單演繹，例如在重構2中，教師引導學生觀察圖形的變化，學生直觀感知了面積在增加，而且內部每增加1枚釘子，圖形邊上的釘子數不變的時候，面積逐步增大了1平方厘米。于是，多維猜測就變成了唯一可能。之后，整合S=n÷2+1，S=n÷2+2，S=n÷2+3……學生不但會類比出S=n÷2+a-1，還可以借助于圖形說出a=1時，即當圖形內部釘子數為1時，面積是S=n÷2，然后每增加一枚釘子，面積要增加1平方厘米。

3.教學有效基于數學本身

“不是教教材，而是用教材教”的理念已經深入人心，雖是至理，只是對數學文本的解讀，不僅是對某一個教材例題知識點進行詮釋，而且是教師要深度理解這一個知識點的“前世”和“未來”，以及在“前世”“當下”和“未來”的這條線中，哪一個點才是核心。

例如“9加幾”的“前世”是數數，“未來”是多位數加減法的算理和加法結合律，其核心點確實是“湊十”。不過，這里的“十”并不是簡單的十個“一”，而是一個不同于“一”的計數單位， 9加幾的學習，其“湊十”的實質是“滿十進一”，將多個1用兩種計算單位組合，是計數的擴張，即數學本身發展的需求。再例如“釘子板上的多邊形”，其“前世”是多邊形面積計算，“未來”是“格點上的面積”，即皮克定理，其核心點是面積規律的逐步概括。但是，這個規律對于其最初的發現者皮克來說，是一個智力游戲；對于小學生來說，“釘子板上的多邊形”的學習是讓學生用數學的眼光觀察世界。

總之，盡管本文的兩個教學案例并不屬于同一個維度，但是帶給教師的教學困惑是一樣的，學生的理解與回答，與教師的所謂精心預設不合拍。當然，由于是不同的教學內容，所以“不合拍”的具體理由自然也是不一樣的，卻帶給了我們相似的啟發：教學預設要講道理；數學教學的有效性離不開數學本身。