雙軸汽車制動力分配因數的優化設計

衛文濤，高　峰

(北京航空航天大學 交通科學與工程學院,北京 100191)

?

雙軸汽車制動力分配因數的優化設計

衛文濤，高峰

(北京航空航天大學 交通科學與工程學院,北京 100191)

摘要：根據制動時整車的受力模型，確定了整車同步附著因數、利用附著因數和制動效率的計算方法。將制動力分配因數作為優化變量，滿載與空載的使用頻率、實際利用附著因數作為考慮因素，提出了一種使整車具有良好制動性的優化方法，得到的優化結果既符合聯合國歐洲經濟委員會(ECE)制動法規的要求，又能保證制動效率不小于70%。本文以某輕型貨車作為分析實例并進行了優化設計，優化結果顯示：在法規要求的速度條件下，制動距離有明顯的減小。

關鍵詞：ECE法規；制動力；分配因數；優化設計

0引言

在車輛制動系統的設計過程中，首先要考慮的就是制動性能。制動系統必須盡可能快地使汽車減速或停止，并且維持汽車在路面上行駛時方向的穩定和可操控[1-4]。前后制動力分配是汽車制動性能很重要的影響因素。文獻[5-6]根據聯合國歐洲經濟委員會(ECE)制動法規求出了前后軸制動力分配比的取值范圍，但結果僅僅滿足了制動法規的要求，并未實現制動性能的最優。文獻[7-9]雖然提出了一種考慮滿載和空載使用頻率的情況下，滿足整車具有良好制動性能的優化方法，但沒有考慮到同步附著因數對于前后軸車輪利用附著因數的影響。實現制動力的合理分配，既要考慮不同載荷的使用頻率，也要考慮同步附著因數對汽車實際使用附著因數的影響。在充分考慮以上兩種影響因素的情況下，本文提出了一種能夠使整車具有良好制動性能的前后制動力分配方法。

1模型的建立

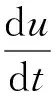
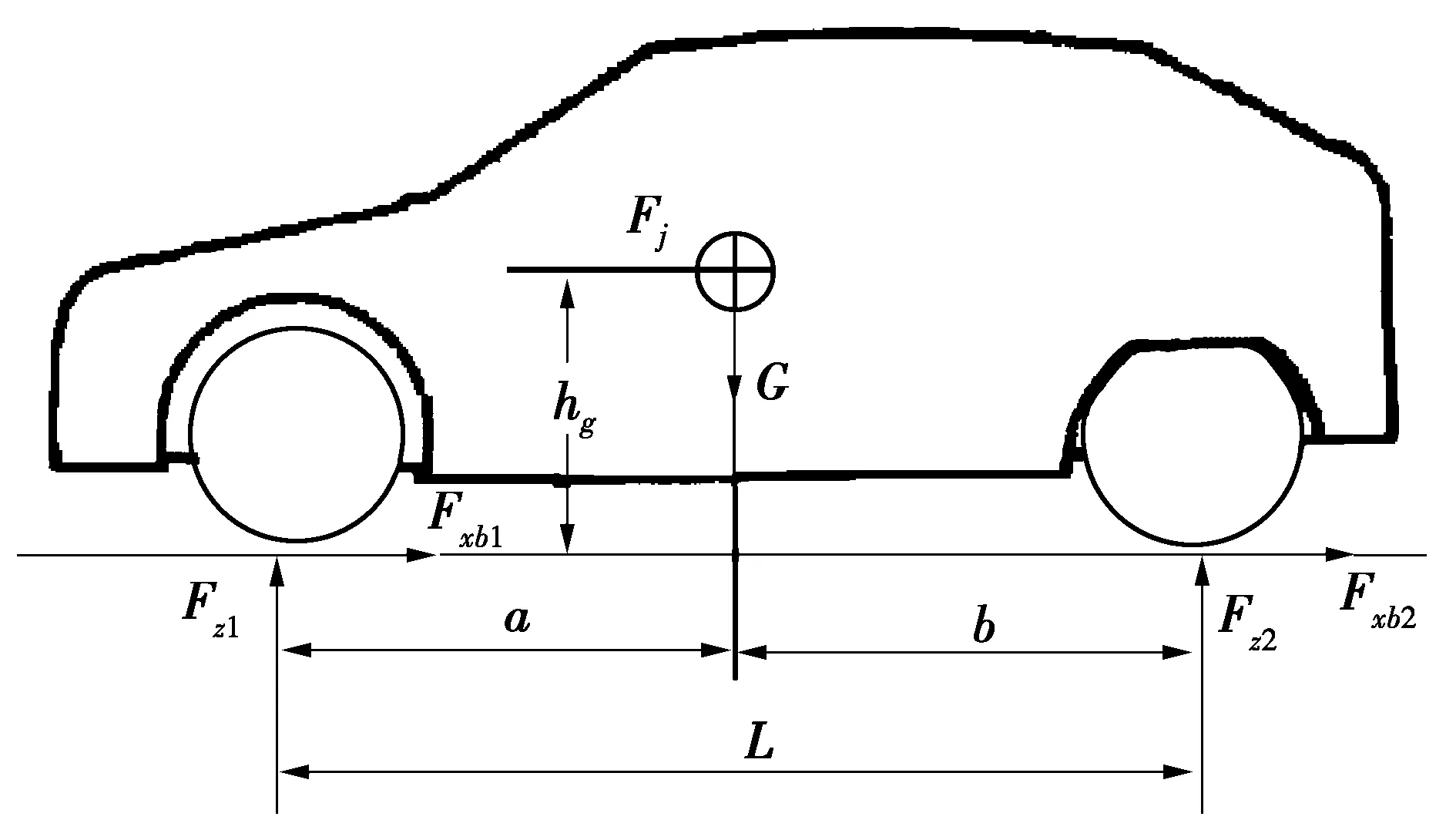
圖1　制動時汽車受力圖

理想制動器制動力分配曲線與實際制動器制動力分配曲線交點處的附著因數稱為同步附著因數，用φ0表示，可得：

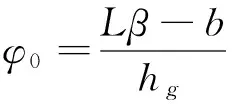
(1)

其中：β為制動力分配因數。

用φi表示汽車的利用附著因數，z表示地面附著因數，則前后軸的利用附著因數分別為：

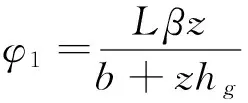
(2)

(3)

制動效率通常也用來描述地面附著因數的利用程度，其值可用來說明制動力分配的合理性。前軸的制動效率為：

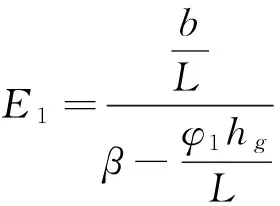
(4)

后軸的制動效率為：

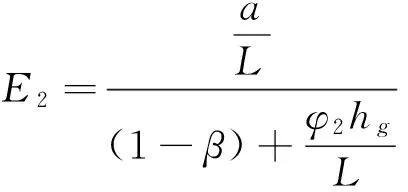
(5)

2制動力分配的優化設計

2.1優化變量的選取

對汽車進行制動時，汽車產生總的制動力，通過前后制動力分配因數β在前后軸之間進行分配。制動力分配因數對前后軸制動力的取值以及制動效率有決定性的影響，因此在優化過程中將β作為變量。

2.2目標函數的確定

汽車以一定的減速度進行制動時，不發生車輪抱死所要求的最小路面附著因數總大于其制動強度(制動強度與地面附著因數相等時除外)。附著因數與制動強度越接近，地面的附著性能發揮得越充分，則汽車的制動力分配合理程度越高[10]。因此，在制動強度范圍內(z=0.15～0.80)，汽車的利用附著因數在盡可能接近車輪剛要抱死需要的利用附著因數時，地面的附著條件發揮得越充分，汽車軸間制動力分配越合理。

在實際設計過程中，考慮到汽車在不同載荷工況下的使用概率存在差異，分別為滿載與空載工況賦予相應的權值，從而實現對不同工況的綜合考慮。在目標函數的實際中，滿載工況的權值設定為w，那么相應的空載工況的權值為(1-w)。

設汽車行駛時的同步附著因數為φ0，則進行制動的路面上φ<φ0時，前輪提前抱死，則在這個范圍內后軸的利用附著因數φ2曲線無意義。因此在φ<φ0時，汽車的利用附著因數曲線應取φ1所確定的曲線。在φ>φ0的路面上制動時，情況正好相反，即φ1曲線無意義。因此φ>φ0時，汽車的利用附著因數應取φ2所確定的曲線[12]。

綜合考慮以上因素，以制動減速度因數z為被積函數的自變量，z的取值范圍為被積函數的積分區間。當φ<φ0時，以汽車前軸實際利用附著因數曲線與理想線間差值的平方和為被積函數；當φ>φ0時，以汽車后軸實際利用附著因數曲線與理想線間差值的平方和為被積函數。以β為優化變量，分別考慮滿載與空載，建立目標函數。通過對目標函數進一步分析，當目標函數取最小值時，所求得β為最優值。

只考慮滿載時的目標函數為：

(6)

只考慮空載時的目標函數為：

(7)

考慮到實際的裝載情況，最終確定的目標函數為：

F(β)=w×P1+(1-w)×P2。

(8)

式(6)～式(8)中：w為滿載工況的權值；φ01和φ02分別為滿載和空載時同步附著因數；φ11和φ21分別為滿載時前、后軸車輪利用附著因數；φ12和φ22分別為空載時前、后軸車輪利用附著因數。

2.3約束條件

(Ⅰ)為了保證制動時汽車的方向穩定性和有足夠的制動效率，ECE R13 制動法規[13]對雙軸汽車前、后輪制動器制動力提出了明確的要求，因此將ECE制動法規作為約束條件。

(Ⅱ)整車的最小制動效率應滿足Emin>70%[7]。

2.4對ECE制動法規的分析

ECE制動法規對各類兩軸車輛的規定[13-14]如下：

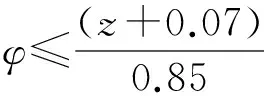
對除M1、N1類型以外車輛有如下規定：(Ⅰ)制動強度z=0.10～0.61，滿足于附著因數φ≤(z+0.07)/0.85。(Ⅱ)當制動強度z=0.15～0.30，若各軸利用附著因數曲線位于由φ=z+0.08和φ=z-0.08確定的兩條平行于理想利用附著因數曲線之間，則認為滿足要求；當z≥0.03時，后軸利用附著因數要滿足φ≤(z-0.02)/0.74。

經過化簡并將滿載和空載情況下的各參數代入以上各種情況，便可初步確定β的取值范圍。

3優化模型的求解及結果

將某輕型貨車作為研究對象，進行制動力分配的優化設計。表1為該車型相關的技術參數[7]。

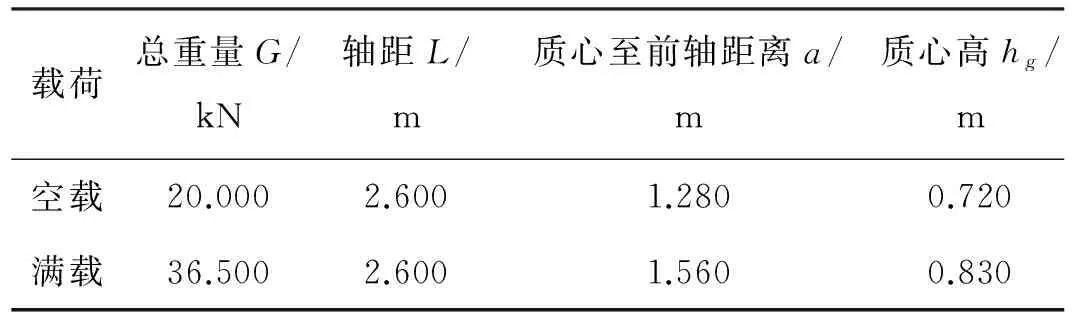
表1　某輕型貨車相關技術參數

利用表1中的數據建立該車的數學模型，根據前面所敘述的方法對該輕型貨車的制動力分配進行優化設計。本文采用的是美國PTC公司旗下的一款工程計算軟件mathCAD，利用mathCAD環境中的求解與優化擴展庫，求解在約束條件下的最優解問題。

由于該車屬于N2類汽車，將相應約束條件代入可得：空載時汽車制動力分配因數的取值為0.576≤β≤0.700；滿載時制動力分配因數的取值為0.469≤β≤0.628。因此，綜合考慮兩種工況，汽車制動力分配因數的約束條件為：0.576≤β≤0.628。

由于在這個制動力分配因數取值范圍內，滿載和空載的同步附著因數均位于區間[0.15，0.80]，從而可通過式(6)和式(7)確定P1、P2的取值，將P1與P2的值代入式(8)可得最終目標函數的形式為：

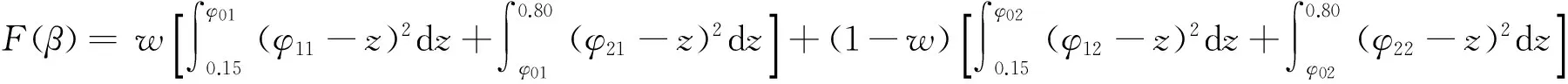
(9)

設定考慮滿載的權重分別為0，0.2，…，1.0，對目標函數的變化趨勢進行分析，將目標函數與制動力分配因數的關系繪制成曲線，如圖2所示。

圖2　目標函數隨制動力分配因數變化曲線

圖2中，在較小滿載權重w的情況下，目標函數的曲線是單調遞減的，因而有單一的最小值，目標函數取最小值時，自變量取上限值為優化結果，此時β=0.628。在較大滿載權重的情況下，目標函數的變化趨勢為一凹形曲線，因此有單一的最小值，在最小值時所對應的制動力分配因數是優化結果。經計算，當w≤0.848時，目標函數為一單調遞減的曲線；當w>0.848時，目標函數為一凹形曲線。因而，使得目標函數達到最小值的優化變量取值如下：當w≤0.848時，使目標函數F(β)取得最小值，所對應的β為0.628；當w=0.900時，使目標函數F(β)取得最小值，所對應的β為0.621；當w=1.000時，使目標函數F(β)取得最小值，所對應的β為0.607。

4結果驗證

4.1ECE制動法規驗證

為了驗證所得的結果是否符合ECE制動法規的要求，將ECE制動法規的曲線和滿載與空載時整車利用附著因數曲線進行對比，其結果見圖3～圖5。經過對比發現：在w取不同值的情況下，滿載與空載優化后的利用附著因數曲線均在ECE制動法規所要求的范圍之內。

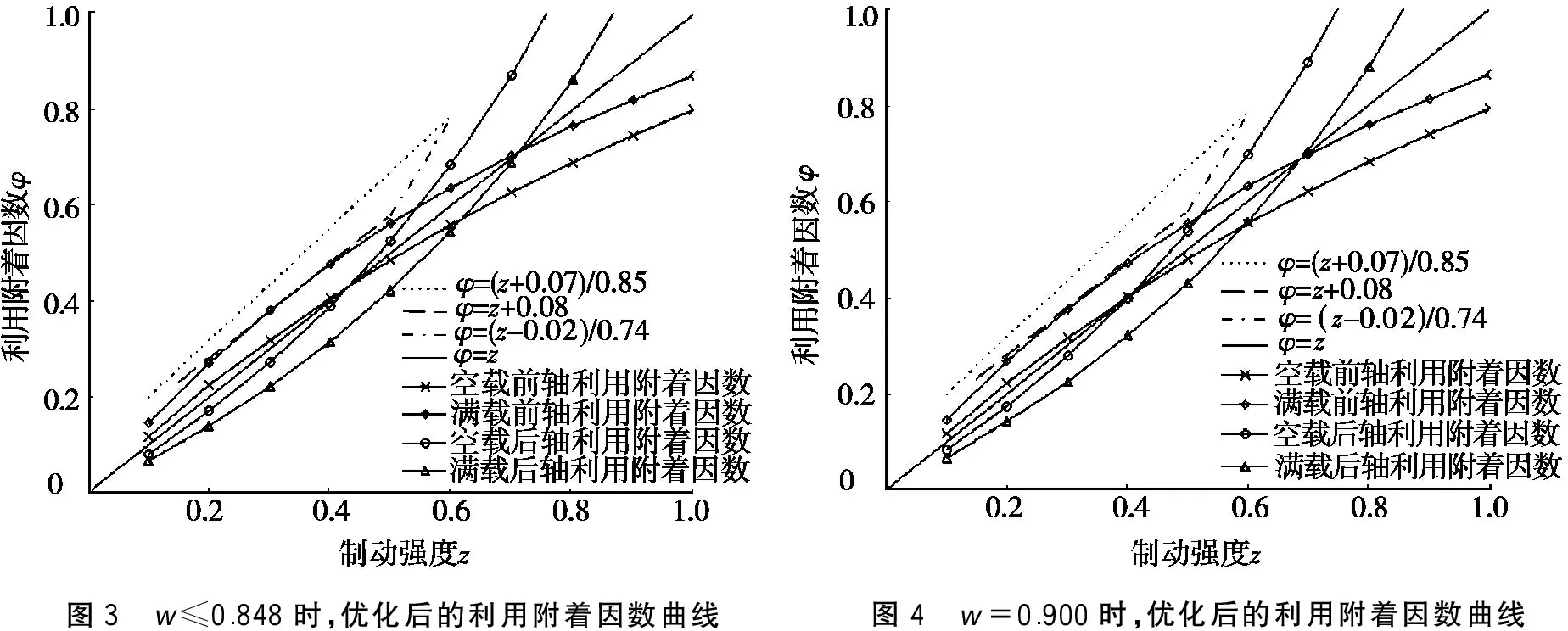
圖3 w≤0.848時,優化后的利用附著因數曲線圖4 w=0.900時,優化后的利用附著因數曲線

4.2制動效率驗證

當w取不同值時，整車的制動效率隨地面附著因數變化見表2～表4。由w取不同值時，所求得的前后軸制動力分配因數β也完全不一樣。由優化后制動效率與地面附著因數的關系可知：w取不同值時，整車滿載與空載狀況時的制動效率均大于70%，達到了約束條件對制動效率的要求。

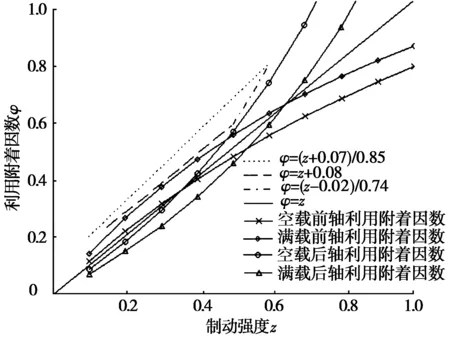
圖5　w=1.000時，優化后的利用附著因數曲線

4.3制動距離驗證

制動距離是制動效能的評價指標。根據制動效率與地面附著因數的關系來確定汽車所能達到的最大減速度，按照下式進行制動距離的計算[15]：

(10)

表2　w≤0.848時，各地面附著因數情況下整車制動效率

表3　w=0.900時，各地面附著因數情況下整車制動效率

表4　w=1.000時，各地面附著因數情況下整車制動效率

為了證明本文優化后的效果，與文獻[7]中的優化后制動距離進行比較，對比結果如表5所示。

表5　優化后制動距離的對比

由表5可知：當w=0.500時，本文優化后制動距離較文獻[7]提出的優化方法，滿載時縮短了0.1 m，空載時縮短了0.3 m。當w=0.750時，本文優化后制動距離較文獻[7]提出的優化方法，滿載時縮短了0.1 m，空載時縮短了0.7 m。當w=1.000時，本文優化后制動距離較文獻[7]提出的優化方法，滿載時縮短了0.3 m，空載時縮短了0.2 m。

通過與文獻[7]中優化方法所得的制動距離的對比，w取不同值時，在法規規定的路面上優化后，該輕型貨車制動距離均小于文獻[7]中優化后所得的制動距離。因此，該車在充分考慮滿載與空載的情況下，優化設計制動效能與整車行駛安全性均能得到提高。

5結論

(1)提出了使各類雙軸車輛制動效能達到最優值時，制動力分配因數β的求解方法。

(2)以某一車型為例進行計算，得到了優化設計的結果，驗證了優化結果既滿足ECE制動法規，也滿足制動效率的要求。

(3)為了驗證所得到的結果是否可以使整車具有更好的制動效能，將優化后的制動距離與文獻[7]所提出方法的優化結果進行對比，表明本文優化方法具有更高的優化效果。

參考文獻：

[1]胡愛軍,王朝暉.汽車主動安全技術[J].機械設計與制造,2010(7):97-99.

[2]BUSCHMANN G,HANS T,KUHN W.Electronic brake force distribution control-a sophisticated addition to ABS[J].SAE paper,1992:920646.

[3]LIMPERT R.Brake design and safety[M].2nd ed.Warrendale:Society of Automotive Engineers,1999.

[4]KIMBROUGH S,ELWELL M.An advanced braking and stability controller for two vehicle and trailer combinations[J].SAE paper,1993:931878.

[5]張立軍,朱博,賈云雷.依ECE法規進行汽車制動力分配新方法[J].遼寧工程技術大學學報,2005,24(2):276-279.

[6]楊啟梁.低速貨車制動力分配因數研究[J].拖拉機與農用運輸車,2006,33(2):65-67.

[7]王亞晴,張代勝,沈國清.汽車制動力分配比的優化設計與仿真計算[J].合肥工業大學報(自然科學版),2005,28(11):1393-1396.

[8]汪文國.農用運輸車制動系優化設計與仿真計算[J].農業機械學報,1998,14(1):108-111.

[9]陳春生.商用車聯合制動系統制動力分配因數的優化[J].機電技術,2013(2):115-118.

[10]余志生.汽車理論[M].北京:機械工業出版社,2001:89-129.

[11]LIAN Y F,TIAN Y T,HU L L,et al.A new braking force distribution strategy for electric vehicle based on regenerative braking strength continuity[J].Journal of central south university,2013,12(20):3481-3489.

[12]劉惟信.汽車制動系的結構分析與設計計算[M].北京:清華大學出版社,2004:44-48.

[13]歐洲經濟委員會.有關M、N和O類車輛制動認證的統一規定[S/OL].2001.http://www.docin.com/p-986856722.html.

[14]方泳龍.汽車制動理論與設計[M].北京:國防工業出版社,2005:32-37.

[15]王宣鋒,應國增,黃朝勝.某微型客車制動力分配優化設計[J].汽車技術,2009(9):1-5.

[16]中國國家標準化管理委員會.機動車運行安全技術條件:GB 7258—2004[S].北京:中國標準出版社,2012:19.

基金項目：國家自然科學基金項目(51275019)

作者簡介：衛文濤(1991-),男,河南項城人,碩士生;高峰(1955-),男,河南洛陽人,教授,博士，博士生導師，主要從事智能車輛/特種車輛及車輛非常規行走機構等方面的研究.

收稿日期：2016-01-30

文章編號：1672-6871(2016)04-0020-06

DOI:10.15926/j.cnki.issn1672-6871.2016.04.005

中圖分類號：U461.3

文獻標志碼：A