灰線性加權非等距GM(1,1)形變預測模型

李克昭　李志偉　丁安民　孟福軍

1　河南理工大學測繪與國土信息工程學院，焦作市世紀路2001號，454000 2　北斗導航應用技術協同創新中心，鄭州市科學大道62號，450001 3　塔里木大學水利與建筑工程學院，阿拉爾市虹橋南路705號，843300

?

灰線性加權非等距GM(1,1)形變預測模型

李克昭1,2李志偉1丁安民1孟福軍3

1河南理工大學測繪與國土信息工程學院，焦作市世紀路2001號，454000 2北斗導航應用技術協同創新中心，鄭州市科學大道62號，450001 3塔里木大學水利與建筑工程學院，阿拉爾市虹橋南路705號，843300

摘要：結合加權非等距GM(1,1)模型與線性回歸理論，構建灰線性加權非等距GM(1,1)預測模型，并給出對模型預測精度起決定性作用的灰指數v和參數m的優化方法。與加權非等距GM(1,1)模型和線性回歸預測模型相比，灰線性加權非等距GM(1,1)預測模型的精度更高，預測有效時間更長，模型的穩定性更好。優化v和m后，灰線性加權非等距GM(1,1)預測模型的實用性、穩定性進一步提高。

關鍵詞：加權非等距GM(1,1)；線性回歸；灰指數v；參數m；變形監測

灰色系統理論可為實測數據有限的建筑物的變形不確定性問題提供新的預測理論支持。用于沉降變形監測的傳統灰色預測模型主要有灰色GM(1,1)模型[1]、優化的灰色GM(1,1)模型[2-3]、灰色人工神經網絡模型[4]、灰色-馬爾科夫預測模型[5]以及灰色組合模型[6-8]等。這些模型都是基于等距時間序列建立的，但在實際的變形監測工作中，時間序列往往是非等距的。基于此，一些學者構建了非等距灰色預測模型，并取得了一定的成果[9-11]。非等距灰色預測模型的預測精度有大幅提高，但依然易受建模數據隨機擾動的影響，且模型的穩定性較差。線性回歸預測模型對短中期的預測能夠取得非常好的效果，具有一定的抗擾動能力。本文從加權非等距GM(1,1)的建模原理入手，結合線性回歸理論建立灰線性加權非等距GM(1,1)預測模型，并將其應用于某建筑物變形監測中，進行預測驗證與比較分析。

1基于加權非等距GM(1,1)和線性回歸理論的預測模型

1.1加權非等距GM(1,1)模型

假設一組非負原始數據序列，記為X(0)：

(1)

式中，tn為觀測時刻，X(0)(tn)為tn時刻的觀測值。

對原始數據X(0)序列進行一次累加，生成的累加數據序列記為X(1)：

(2)

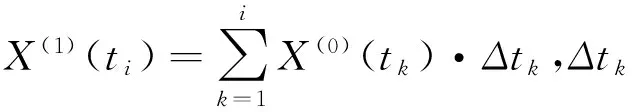
參考文獻[9-11]，利用最小二乘原理計算可得加權非等距GM(1,1)的預測方程為： [7-8]，由灰色GM(1,1)預測方程可得：

(3)

最后，恢復時間序列，還原預測值：

(4)

1.2灰線性加權非等距GM(1,1)預測模型

(5)

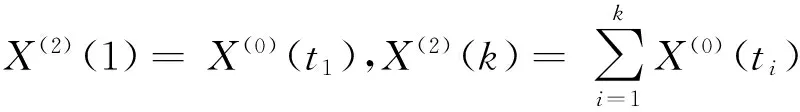
(6)

式中，a1為發展系數，b1為灰作用量。式(6)可記為：

(7)

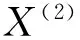
(8)

式中，參數v、m1、m2、m3為待定系數，為確定的4個參數。設參數序列：

(9)

由式(9)可求得參數v的解為：

v=ln(Ym(t+1)/Ym(t))

(10)

(11)

將式(11)的計算結果進行一次累減，還原時間序列，生成原始序列X(0)的擬合值和預測值。由式(11)可知，當m1=0時，該預測方程為線性回歸方程；當m2=0時，該預測方程為傳統的GM(1,1)預測方程。灰線性加權非等距GM(1,1)模型使加權非等距GM(1,1)模型中不含線性因素以及線性回歸中不含指數增長趨勢的情形得

到很好的改善。

2實例計算與分析

以文獻[8]中居民樓1棟CJ1沉降點的沉降累計觀測數據為例(表1)，利用前8期沉降數據構建灰線性加權非等距GM(1,1)預測模型，預測第9～13期沉降數據，并與加權非等距GM(1,1)預測模型、線性回歸預測模型進行比較(表2)。

2.1數據計算與分析

從表2可以看出，灰線性加權非等距GM(1,1)預測模型的預測值殘差中誤差遠小于加權非等距GM(1,1)和線性回歸預測模型。加權非等距GM(1,1)和線性回歸預測模型在短期內預測效果較好，但隨著預測時間的增加，預測效果越來越來差。相比而言，灰線性加權非等距GM(1,1)預測模型精度更高，穩定預測時間更長。

2.2m、v取值對模型預測精度的影響

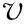
由表4和表5可知，對于建模數據n=7，當m=1，2，3，4時，該模型的預測擬合值精度最優；對于n=8，當m=1,2,3,4,5時，該模型的預測擬合值精度最優。m的取值隨著建模數據維數的不同而變化，但并非m值越大，模型的預測精度就越高。由于各個建模數據具有一定的隨機擾動性，因此，在實際建模過程中，應根據建模數據的不同進行討論，并計算出最優的預測模型。

2.3預測結果分析

n值不同，模型的預測精度也不相同，預測精度的不同是因為不同的建模條件對模型系統特征的影響不同。由表4和表5可知，當n=7,m=1，2，3，4時，該模型在n=7條件下預測精度最優；當n=8,m=1,2,3,4,5時，該模型在n=8條件下預測精度最優。將兩種模型都進行5期預測，結果見表6。

從表6看出，當n=8,m=1,2,3,4,5時，該模型最適合原始的建模數據，模型的預測精度最高，殘差中誤差為1.900 5 mm，同時證明了該預測模型具有預測精度高、預測周期長的優勢。所以，在模型建立時，應根據建模數據的不同進行討論，建立最優的預測模型。

3結語

[1]李年奇,張俊中. GM(1，1)模型在建筑物變形監測中的應用[J]. 測繪與空間地理信息,2013,36(8):258-260(Li Nianqi, Zhang Junzhong. Application of GM(1,1) Forecast in the Deformation of Building[J]. Geomatics & Spatial Information Technology, 2013,36(8):258-260)

[2]袁德寶, 崔希民, 高寧. 同時利用x(1)(1)和x(1)(n)為GM(1,1)建模初始條件的預測方法研究[J]. 大地測量與地球動力學, 2013, 33(3):79-82 (Yuan Debao, Cui Ximin, Gao Ning. A Forecast Method Combiningx(1)(1) withx(1)(n) as Initial Value of GM(1,1) Model[J]. Journal of Geodesy and Geodynamics, 2013, 33(3):79-82)

[3]王康, 周世健. 初始條件改進全概括灰色理論預測模型研究[J]. 測繪科學, 2014, 39(12):29-32(Wang Kang, Zhou Shijian. Study on Gray Prediction Model of Summarizing All the Initial Condition Improvements[J]. Science of Surveying and Mapping, 2014, 39(12):29-32)

[4]郭蘭蘭,鄒志紅,安巖.基于灰色神經網絡模型的水質預測應用研究[J].數學的實踐與認識,2015,45(5):89-93(Guo Lanlan, Zou Zhihong, An Yan. Study on Grey Model Combined with Artificial Neural Networks Model for Water Quality Forecast[J]. Mathematics in Practice and Theory, 2015,45(5):89-93)

[5]沈哲輝,黃騰,唐佑輝.灰色-馬爾科夫模型在大壩內部變形預測中的應用[J].測繪工程,2015,24(2):69-74(Shen Zhehui, Huang Teng, Tang Youhui. Application of Grey Markov Model in Dam Internal Horizontal Displacement Prediction[J]. Engineering of Surveying and Mapping, 2015,24(2):69-74)

[6]文鴻雁,周呂,韓亞坤,等. 基于卡爾曼濾波的GM(1,1)模型在高鐵隧道沉降變形分析中的應用[J]. 大地測量與地球動力學,2014,34(1):88-91(Wen Hongyan, Zhou Lü, Han Yakun, et al. Application of GM(1,1) Model Based on Kalman Filter to the Subsiding Analysis of High-Speed Railway Tunnel[J]. Journal of Geodesy and Geodynamics, 2014,34(1):88-91)

[7]高寧,崔希民,高彩云.高層建筑物沉降變形的灰線性預測[J].測繪科學,2012,37(3):96-98(Gao Ning, Cui Ximin, Gao Caiyun. Application of GM(1,1) and Line Regression for Predicting Subsidence and Deformation High Building[J]. Science of Surveying and Mapping, 2012, 37(3):96-98)

[8]張俊中,雷偉偉,王睿,等.灰線性回歸模型在建筑物沉降分析中的應用[J].河南科學,2015,33(3):416-420(Zhang Junzhong, Lei Weiwei, Wang Rui, et al. Application of GM(1,1) and Line Regression Model in the Deformation of Building[J]. Henan Science,2015,33(3):416-420)

[9]成樞,李強.基于非等間隔GM(1,1)模型的沉降預測[J].測繪與空間地理信息,2015,38(4):33-35(Cheng Shu, Li Qiang. Based on Non-GM(1,1) Model Settlement Prediction Intervals in Foundation Ditch[J]. Geomatics & Spatial Information Technology, 2015,38(4):33-35)

[10]陳鵬宇,段新勝. 建筑物沉降的非等間隔GM(1,1)模型的建立與改進[J]. 工程勘察,2010,38(3):77-80(Chen Pengyu, Duan Xinsheng. Establishment and Improvement of Non-Equal Interval GM(1,1) Model of Building Subsidence[J]. Geotechnical Investigation & Surveying, 2010,38(3):77-80)

[11]李軍亮,肖新平,廖銳全.非等間隔GM(1,1)冪模型及應用[J].系統工程理論與實踐,2010,30(3):490-495(Li Junliang, Xiao Xinping, Liao Ruiquan. Non-Equidistance GM(1,1) Power and Its Application[J]. Systems Engineering-Theory & Practice, 2010,30(3):490-495)

Foundationsupport:NationalNaturalScienceFoundationofChina,No. 41202245, 41272373;BackboneTeacherFoundationofHenanPolytechnicUniversity,No.72105/090.

Aboutthefirstauthor:LIKezhao,PhD,associateprofessor,majorsinsatellitepositioningandvisionnavigationtheory,E-mail:lkznwpu@126.com.

Deformation Prediction Model of Gray Line Weighted Non-Equidistance GM(1,1)

LIKezhao1,2LIZhiwei1DINGAnmin1MENGFujun3

1School of Surveying and Land Information Engineering, Henan Polytechnic University, 2001 Shiji Road, Jiaozuo 454000, China 2Collaborative Innovation Center of BDS Research Application, 62 Kexue Road, Zhengzhou 450001, China 3College of Water Resources and Architectural Engineering, Tarim University, 705 South-Hongqiao Road, Alar 843300, China

Abstract:On the basis of weighted non-equidistance GM(1,1) and line regression theories, we combined a weighted non-equidistance GM(1,1) model with line regression theory organically, and propose

thegraylinearweightednon-equidistanceGM(1,1)model.Thentheoptimizationmethodofthegrayindexvandthevalueofparameterm,whicharevitaltothemodelpredictionaccuracy,isgiven.Incomparisonwiththeweightednon-equidistanceGM(1,1)andlineregressionmodels,thegraylinearweightednon-equidistanceGM(1,1)modelhasadvantages,suchashigherpredictionaccuracy,morevalidpredictiontime,andmorestablepredictionability.Whenvandmareoptimized,theapplicabilityandstabilityofthegraylinearweightednon-equidistanceGM(1,1)modelisfurtherimproved.

Keywords:weightednon-equidistanceGM(1,1);lineregression;greyindexv;parameterm;deformationmonitoring

收稿日期：2015-09-22

第一作者簡介：李克昭，博士，副教授，主要從事衛星定位和視覺導航的理論研究，E-mail: lkznwpu@126.com。

DOI：10.14075/j.jgg.2016.06.010

文章編號：1671-5942(2016)06-0513-04

中圖分類號：P258

文獻標識碼：A

項目來源：國家自然科學基金(41202245，41272373)，河南理工大學骨干教師資助項目(72105/090)。