基于雙曲線模型的卡爾曼濾波法在建筑物沉降預測中的應用

陸付民　蔣廷耀

1　三峽大學三峽庫區地質災害教育部重點實驗室，宜昌市大學路8號，443002 2　中國礦業大學國土環境與災害監測國家測繪地理信息局重點實驗室， 徐州市大學路1號，221116 3　三峽大學計算機與信息學院，宜昌市大學路8號，443002

?

基于雙曲線模型的卡爾曼濾波法在建筑物沉降預測中的應用

陸付民1,2蔣廷耀3

1三峽大學三峽庫區地質災害教育部重點實驗室，宜昌市大學路8號，443002 2中國礦業大學國土環境與災害監測國家測繪地理信息局重點實驗室， 徐州市大學路1號，221116 3三峽大學計算機與信息學院，宜昌市大學路8號，443002

摘要：利用最小二乘法求出雙曲線模型的模型參數，將此參數看作帶有動態噪聲的狀態向量，建立基于雙曲線模型的卡爾曼濾波模型，對建筑物的沉降量進行預測。卡爾曼濾波過程中，模型的參數不斷發生變化，增強了其適應觀測數據的能力，從而減小了擬合誤差。計算表明，用基于雙曲線模型的卡爾曼濾波模型對建筑物的沉降量進行預測，誤差較小，效果較為理想。

關鍵詞：雙曲線模型；卡爾曼濾波；動態噪聲；沉降；預測

為了保證建筑物的安全運營，需要定期對建筑物進行沉降觀測，獲取沉降觀測數據，建立擬合精度及預測精度較高的預測模型。雙曲線模型將模型參數作為定值，在一定程度上限制了其適應觀測數據的能力，因此擬合誤差較大，預測效果不太理想。為了提高模型的擬合精度及預測效果，將雙曲線模型的模型參數作為帶有動態噪聲的狀態向量，建立基于雙曲線模型的卡爾曼濾波模型，并以此為基礎對建筑物的沉降量進行預測。算例表明，本文模型擬合誤差較小，預測效果也較為理想。

1雙曲線模型

雙曲線模型可以寫為[1]：

(1)

式中，S0為建筑物的初期沉降量，t 為觀測時刻，a和b為雙曲線模型的模型參數，St為t時刻建筑物的沉降量。

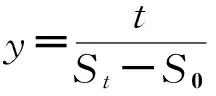
y=a+bt

(2)

根據沉降觀測序列，由最小二乘法即可求出模型參數a和b，進而對建筑物的沉降量進行預測。

2卡爾曼濾波模型

離散線性系統的卡爾曼濾波模型的狀態方程和觀測方程分別為[2-10]：

(3)

(4)

式中，Xk和Lk分別為tk時刻的狀態向量和觀測向量，Φk+1,k為tk時刻至tk+1時刻的狀態轉移矩陣，Bk+1為tk+1時刻的觀測矩陣，Ωk和Δk分別為tk時刻的動態噪聲和觀測噪聲。

卡爾曼濾波模型的隨機模型為[2-10]：

(5)

式中，E(Ωk)為Ωk的數學期望，E(Δk)為Δk的數學期望，cov(Ωk,Ωj)為Ωk與Ωj的協方差，DΩ(k)為Ωk的方差，cov(Δk,Δj)為Δk與Δj的協方差，DΔ(k)為Δk的方差，cov(Ωk,Δj)為Ωk與Δj的協方差，E(X0)為X0的數學期望，var(X0)為X0的方差，cov(X0,Ωk)為X0與Ωk的協方差，cov(X0,Δk)為X0與Δk的協方差。當j=k時，δkj=1 ；當j≠k時，δkj=0。

由狀態方程、觀測方程和隨機模型，即可推出如下卡爾曼濾波方程[2-10]：

(6)

式中，I為單位矩陣，且

(7)

3基于雙曲線模型的卡爾曼濾波模型

為了提高雙曲線模型的擬合精度，將雙曲線模型的參數a和b作為帶有動態噪聲的狀態向量，用卡爾曼濾波法進行濾波，求出狀態向量的最佳估值，最后進行建筑物沉降量的預測。為此，建立如下模型：

(8)

則式(8)變為：

(9)

式(9)即為相應的觀測方程。為了便于卡爾曼濾

波，將Xk看作包含有動態噪聲的狀態向量，則有Xk+1=Xk+Ωk,即

(10)

式中，Φk+1,k=I，即Φk+1,k為單位矩陣。根據式(9)和式(10)，得出卡爾曼濾波模型的狀態方程和觀測方程：

(11)

根據式(11) 并顧及式(5)，由式(6)即可求出tk時刻a和b的濾波值，由a和b即可求出卡爾曼濾波模型的擬合值，進而求出沉降量的擬合值。

4算例

注：殘差為模型的擬合值與觀測值之差。

由表1可以看出，雙曲線模型的殘差相對較大，最大為0.924 mm，最小為-0.027 mm。而本文模型殘差均小于0.33 mm，最大殘差為0.328 mm，最小殘差為0.004 mm，表明本文模型擬合精度較高。另外，本文模型正負殘差基本各占一半，表明其具有隨機性。

雙曲線模型預測J6點2013-12的沉降量為23.608 mm，而J6點2013-12的沉降觀測值為 24.03 mm，預測誤差為-0.422 mm，預測誤差相對較大；本文模型預測J6點2013-12的沉降量為24.211 mm，預測誤差為0.181 mm，預測誤差相對較小，預測效果較好。

5結語

本文將雙曲線模型的模型參數作為狀態向量，建立基于雙曲線模型的卡爾曼濾波模型，并將該模型用于建筑物的沉降預測。結果表明，本文模型的適應性較強，建模精度及變形預測精度較高，預測效果較為理想。

參考文獻

[1]陳剛. 建筑物沉降變形監測數據處理與預測方法研究[D].贛州:江西理工大學，2011(Chen Gang. Study about Data Processing and Forecast Method for Settlement Deformation Monitoring of Buildings[D]. Ganzhou：Jiangxi University of Science and Technology，2011)

[2]周樂韜，黃丁發，袁林果，等.網絡RTK參考站間模糊度動態解算的卡爾曼濾波算法研究[J].測繪學報，2007，36(1)：37-42(Zhou Letao，Huang Dingfa，Yuan Linguo，et al. A Kalman Filtering Algorithm for Online Integer Ambiguity Resolution in Reference Station Network[J]. Acta Geodaetica et Cartographica Sinica，2007，36(1)：37-42)

[3]崔希璋，於宗儔，陶本藻，等.廣義測量平差[M].北京：測繪出版社，1992(Cui Xizhang，Yu Zongchou，Tao Benzao，et al. General Surveying Adjustment[M]. Beijing: Surveying and Mapping Press，1992)

[4]王正明，易東云. 測量數據建模與參數估計[M].長沙：國防科技大學出版社，1997(Wang Zhengming，Yi Dongyun. Modeling of Surveying Data and Parameter Estimation[M]. Changsha: National Defense Science and Technology University Press，1977)

[5]陸付民，何薪基.基于模型篩選法的卡爾曼濾波法在大壩變形分析中的應用[J].水電自動化與大壩監測，2003，26(4)：55-57(Lu Fumin，He Xinji. Application of Model Screening Based on Kalman Filter Method to Dam Deformation Analysis[J]. Hydropower Automation and Dam Monitoring，2003，26(4)：55-57)

[6]陸付民.模型優化法在滑坡變形分析中的應用[J].勘察科學技術，2003，21(2)：48-51(Lu Fumin. Application of the Model Optimization Method in the Landslide Deformation Analysis[J]. Investigation Science and Technology ，2003，21(2)：48-51)

[7]陸付民，李勁.顧及時間及開挖深度的卡爾曼濾波模型在建筑物變形分析中的應用[J].測繪通報，2012(2)：59-61(Lu Fumin，Li Jin. Application of Kalman Filter Model with the Time and Excavation Depth to Building Deformation Analysis[J]. Bulletin of Surveying and Mapping，2012(2)：59-61)

[8]陸付民. 基于AR(n)模型的卡爾曼濾波模型[J].數學的實踐與認識，2007，37(19)：6-11(Lu Fumin.Kalman Filter Model Based on AR(n) Model[J]. Mathematics in Practice and Theory，2007，37(19)：6-11)

[9]徐亞明，劉冠蘭，柏文峰.顧及基坑施工影響的地鐵區間隧道結構卡爾曼濾波預測模型[J].武漢大學學報:信息科學版，2013，38(11) ：1 322-1 325(Xu Yaming，Liu Guanlan，Bai Wenfeng. Kalman Filter Model Considering Pit Construction Simulation Evaluation for Tunnel Deformation Prediction[J]. Geomatics and Information Science of Wuhan University，2013，38(11) ：1 322-1 325)

[10]高雅萍，馮曉亮. 離散性卡爾曼濾波在GPS變形監測數據處理中的應用[J].工程勘察，2006(7)：55-57(Gao Yaping，Feng Xiaoliang. Application of Discrete Kalman Filter in GPS Deformation Monitoring Data Processing[J]. Journal of Geotechnical Investigation and Surveying，2006(7)：55-57)

Foundation support:National Natural Science Foundation of China, No.41172298；Open Fund of Key Laboratory of Land Environment and Disaster Monitoring, NASMG, No.LEDM2013B03.

About the first author:LU Fumin，professor，majors in deformation monitoring and data processing，E-mail：lfm640929@ctgu.edu.cn.

Application of Kalman Filter Method Based on Hyperbolic Curve Model in the Settlement Forecast of Building

LUFumin1,2JIANGTingyao3

1Key Laboratory of Geological Hazards on Three Gorges Reservoir Area of Ministry of Education， hree Gorges University，8 Daxue Road，Yichang 443002，China 2Key Laboratory of Land Environment and Disaster Monitoring，NASMG,China University of Mining and Technology，1 Daxue Road，Xuzhou 221116，China 3Computer and Information College，Three Gorges University，8 Daxue Road，Yichang 443002，China

Abstract:We construct the hyperbolic curve model and then use the least square method to obtain its parameters. These parameters are regarded as state vectors to contain dynamic noises to erect a Kalman filter model based on the hyperbolic curve model. On the basis of this model we forecast settling amounts of the building. Since the parameters of the Kalman filter model change continuously, its ability to suit the observation data is increased, and the fitting error of the model is reduced. An example of calculation shows that the forecast error is small, and this suggests that it is best to use the Kalman filter model based on the hyperbolic curve model to forecast settling amounts of the building.

Key words:hyperbolic curve model; Kalman filter; dynamic noises; settlement; forecast

收稿日期：2015-06-11

第一作者簡介：陸付民，教授，主要從事變形監測及其數據處理研究，E-mail：lfm640929@ctgu.edu.cn。

DOI：10.14075/j.jgg.2016.06.011

文章編號：1671-5942(2016)06-0517-03

中圖分類號：P258

文獻標識碼：A

項目來源：國家自然科學基金(41172298)；國土環境與災害監測國家測繪地理信息局重點實驗室開放基金(LEDM2013B03)。