高中物理教學中臨界思維的培養

董存生

“狀態”認識是研究物理規律的首要任務，對高中學生而言，狀態分析是正確解題的前提，也是體現新課程理念下學生自主解決問題的基本能力。臨界思維在物理學思維訓練中相對困難，因為涉及到研究對象微妙狀態的抽取，而且需將該“微妙”狀態與基本理論相結合，找到能夠定量求解的途徑。高中物理教學中臨界思維的培養必須以構建臨界狀態為基礎，尤其對于高中力學、運動學章節而言，狀態問題直接與受力問題相關，因此對臨界點的把握至關重要。具體而言，物理教學中臨界思維的培養是將物理問題微觀化，進而將某個特定的物理過程轉化為數學問題，進而能夠將抽象的物理現象轉化為具體的數學方程進行求解。

一、高中物理中典型的臨界思維

臨界思維的應用基礎在于臨界狀態的認識，通俗地講，臨界狀態也稱為邊界狀態，是指研究對象在某個力的作用下從一種狀態即將過渡到另一種狀態，該“臨界點”處研究對象具有典型的物理規律，通常能夠將該狀態與教材基本理論發生對應，進而列出具體的理論公式。某種意義上，臨界思維的運用對解題起到承前啟后的作用，因此所對應的物理規律具備連續性，亦即該狀態所具備的能量、速度、受力情況以及對應的動力學、靜力學、運動學等規律具備前后連續性，為成功解題提供了諸多已知元素。

1.復雜力學場中臨界思維的運用

電磁場涉及到的運動學是高中物理學中難度較大的章節，成功解題的前提要求學生掌握全面的電磁學以及力學綜合知識，然而對該類綜合性力學場問題的求解必須通過恰當的物理思維進行梳理，通常臨界思維是解決復合場問題的有效途徑。

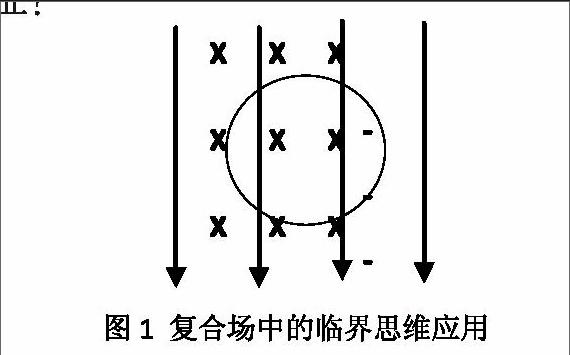
例如，如圖1存在豎直向下的電場，其強度為E；同時，存在垂直紙面向里的勻強磁場，磁感強度為B。一帶電小球m在該復合場中運動，如果該小球在垂直于磁場的豎直平面內做恰好勻速圓周運動，軌道半徑為R。則該小球帶何種類型的電荷？試描述其運動特征？

分析：本題中屬于典型的復雜受力模型，未知電性的帶電小球至于其中能夠“恰好”做勻速圓周運動，是本題應用臨界思維的突破口。首先，使得小球在豎直平面做勻速圓周運動的前提是豎直向上的方向上存在作用力，并且該作用力與重力平衡。根據題設已知豎直方向上存在勻強電場，因此電場力與重力平衡后使得小球僅在洛倫茲力的作用下勻速圓周運動。據此在結合小球的運動軌跡不難判斷出小球帶負電。

本題中，臨界狀態可以視為“恰好”做勻速圓周運動，可以根據圓周運動進行確立，亦即帶負電的小球做圓周運動的軌跡特征取決于洛倫茲力的方向和大小，進而列出力學方程。由于帶負電，電場方向豎直向下，因此可以根據左手定則確定只有當電子順時針運動時才能產生如圖所示的圓周軌跡。

2.斜面受力模型中的臨界思維

高中物理學科中的邊界問題通常涉及力學、運動學知識，通常解題技能的高低取決于對力學模型的自我總結與歸納。其中斜面上力學問題是高中物理中最常見的受力分析模型之一。該模型中主要以力學受力分析為主線，應用到力在不同方向的正交分解等。然而復雜的斜面問題往往將研究對象的狀態復雜化，譬如涉及到動態的斜面問題時，傳統的受力分析很難找到有效的定量關系，此時臨界思維能夠發揮有效作用。眾所周知，物體狀態由所受的外力情況決定，因此臨界問題歸根結底是研究物體受力的臨界情況，主要是體現物體受力平衡的情況即將被破壞或者即將不被破壞的微妙狀態。從力學角度分析臨界狀態能夠很直觀的列出受力平衡方程，借助常規的數學處理技巧即可較為容易的完成力學問題的求解。

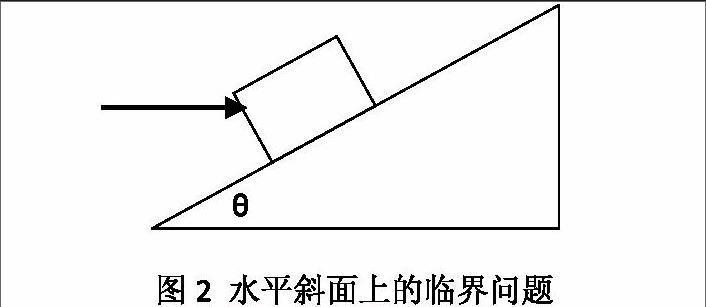
例如，傾角為θ的粗糙斜面上（動摩擦因數為μ

分析：本題中的臨界狀態應該抓住關鍵字眼“恰好”靜止于斜面，意味著推力F的施加與其他未知力的綜合效果使得物理靜止于此。然而，此時物體靜止并非不具備運動的趨勢，如果能夠從此臨界狀態中探究出運動趨勢與F滿足的條件存在關系，就能夠使得臨界思維發揮最大的效用。

靜止意味著物體可能具備沿斜面向上的運動趨勢，也可能具備沿斜面向下的運動趨勢，根據不同方向的運動趨勢可以確定推力F的范圍，在具體求解中可以沿著斜面進行F的正交分解，再根據臨界狀態所要求的力學平衡，沿斜面方向上受力平衡，并且該臨界狀態下斜面產生的最大靜摩擦力可以認為等于滑動摩擦力，繼而列出力學平衡方程即可。

顯然，該題對于斜面問題的臨界狀態是圍繞平衡力展開，然而，對靜止的物體運動趨勢的判斷中，有效采用了臨界思維，使得對物體潛在運動趨勢的分析更加全面，充分挖掘出了“恰好”靜止在斜面上的隱含信息，進而有效提升了學生自主解決問題的能力。

二、結語

臨界思維的培養是新課程理念下技能培養的有效途徑，通過臨界思維能夠挖掘題目隱含的物理學規律，是成功解題的中樞紐帶。高中物理教學中典型復合場問題以及斜面問題處理是鍛煉學生邊界思維的有效模型，通過對特殊狀態的抽取，尋找定量的力學方程，進而使得臨界問題成為解題的突破口。

（作者單位：江蘇省漣水中學）