《離散型隨機變量及其分布列》教學再認識

馮 法

（新疆維吾爾自治區烏魯木齊市外國語學校第十二中學，新疆烏魯木齊 830006）

一、離散型隨機變量的分布列的概念

概念的內涵指的是概念所反映對象的本質特征。

數學概念的教學應從創設概念生長點的問題情境切入探究。“問題是數學的心臟”，數學活動是由“情景問題”驅動的，“問題解決”是其主要的活動形式，創設可以連續變式的正多面體的問題情境，提出從低緯度向高緯度發展的問題是歷經數學概念再創造的好的開始。層層遞進的過程中，逐步豐富和建構對概念中位數本質意義的理解，即將“促進學生理解”始終貫串在整個課堂中。

引入隨機變量的概念，是把對隨機現象統計規律的研究數學化，從而可以利用數學方法研究隨機現象的規律性。其中對隨機變量的概率分布的研究是實現這種轉化的關鍵。

本節的內容“分布列”是一種列舉方式，是將試驗結果整理的過程。在這個表格中，我們可以直觀的找到某一事件所對應的片段，進而對整個試驗有較為完整的認識。

例如：一袋中裝有5只球，編號為1，2，3，4，5，在袋中同時取3只，以ξ表示取出的三只球中的最小號碼，寫出隨機變量ξ的分布列.

首先，明確試驗結果的可能性，然后再給予隨機變量的取值。其中第一行中每個數字的含義給出更為具體的解釋，如：“4”表示最小號碼為4。在此基礎上，根據隨機變量相應的取值，求對應的概率。

對應練習：

判斷下列表格是否可以作為分布列：

?

?

?

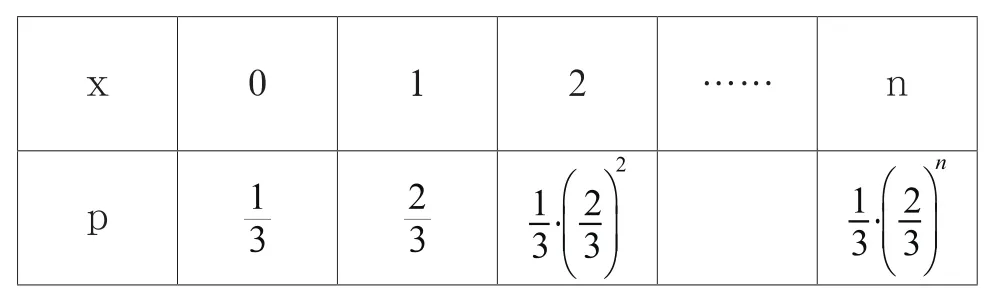
二、對分布列的應用探究

概念的外延指的是概念所反映的本質屬性的對象，概念的內涵是質的方面，概念的外延是概念量的方面，它說明概念所反映的事物有哪些。

離散型隨機變量的分布列的性質是概念的外延，而離散型隨機變量的概率分布列的內涵是一個必然事件分解成有限個互斥事件的概率的另一種表示形式，更主要的是應在概念的生成中形成解決問題的思維方法。

借助于“引導式”教學、采用“剝洋蔥皮”的方式從概念的外延出發探尋其內涵。循序漸進，逐層推進。基于此，設置問題，引發學生的思考。

問題1：通過簡單的離散型隨機變量的分布列，學生交流歸納并驗證分布列具有哪些性質。

其中，性質2的理解是本節課的一個難點，結合實例，設置如下問題串：

道路因素實際上是目前車載導航主要考慮的方面。車載導航通過內置的地圖匹配，即map matching功能，將實時定位的電動汽車位置與實際道路相匹配，便可獲取車輛當前行駛道路的信息，從而完成實時路徑規劃[9]。事實上，在對電動汽車出行路徑進行規劃時，道路實時條件是出行時間的一大組成部分。

例：若某隨機變量ξ的分布列如表所示

3456

問題2：性質2的含義是什么？

問題3：每一個分布列有多少個隨機事件？

問題4：隨機事件之間是什么關系？

問題5：這些隨機事件構成的復雜事件又表示什么事件？

問題6：在擲一枚硬幣的隨機試驗中，令如果正面向上的概率為P，隨機變量X的分布列應該怎么表示？

對應練習：

1.隨機變量ξ的分布列為

（1）求常數a；

（2）求P(1＜ξ＜4)

2.拋擲兩枚骰子，點數之和為X，請列出變量分布表，并求點數之和為3的倍數的概率。

3.某城市有甲、乙、丙3個旅游景點，一位客人游覽這3個景點的概率分別是0.4，0.5，0.6，且客人是否游覽哪個景點互不影響.設ξ表示客人離開該城市時游覽的景點數與沒有游覽的景點數之差的絕對值.

(1)求ξ的分布列及數學期望；

(2)記“函數 在區間(2，＋∞)上單調遞增”為事件A，求事件A的概率.

三、教學上要做整體的把握，應該從基本點出發，形成交匯點，進而達到制高點

教學的基本點就是“雙基”：數學基礎知識和基本技能。從雙基出發，使得基礎知識形成網絡、基本技能形成規律。制高點是重點，是可以達到必要深度的部分，但又不僅僅是重點。重點只是數學的結果，不指向如何應對；而制高點致力于探尋問題解決的基本思路，形成解決問題的方法和規律。站在制高點上進行教學設計，就是首先要準備貫徹什么樣的教學理念、采用什么樣的教學方法為支撐下的教學設計。所以在教學時應重視情境預設、更重視思維的發展歷程，關注知識的內化、更關注形成知識的方法的理性建構，努力對課堂教學不斷地進行積極的、有意義的開發與探索。

[參考文獻]

[1] 中華人民共和國教育部.普通高中數學課程標準[S].北京：人民教育出版社，2003.

[2] 廖金祥，朱晴晴.“直線的一般式方程”的教學分析及教學思考[J].中學數學教學參考，2015，19：29-31+34.

[3] 方厚良，羅燦.泰勒的思維“六步驟”范式及其應用[J].中學數學教學參考，2015，28：29-31.

[4] 田載今.“離散型隨機變量”的教學設計之我見[J].中小學數學(高中版)，2010，04：37-39.