空間繩網二級發射模式動力學分析

高慶玉，唐乾剛，張青斌，豐志偉（國防科學技術大學航天科學與工程學院，湖南長沙410073）

?

空間繩網二級發射模式動力學分析

高慶玉，唐乾剛，張青斌，豐志偉
（國防科學技術大學航天科學與工程學院，湖南長沙410073）

摘要：借鑒降落傘“先拉出、后展開”思想，提出一種空間繩網二級發射模式，并建立了數值仿真模型。該發射模式將繩網拉出展開過程分解為拉出和展開兩個步驟，進行分步控制，保證了繩網規則、有序地拉出，避免了繩網拉出展開過程中的纏繞、穿透和打結等問題。將數值仿真結果與地面試驗數據進行對比，驗證了該模型的有效性和可用性。空間繩網二級發射模式的提出與仿真模型的建立為空間繩網發射優化設計提供了一種參考途徑。

關鍵詞：飛行器發射與回收、飛行技術；空間繩網；動力學建模；二級發射；數值仿真；優化設計

高慶玉（1985—），男，博士研究生。E-mail：gao. qing. yu@163. com

0 引言

空間繩網技術利用柔性繩網捕獲目標的方法回收廢棄的航天器及碎片，是伴隨著空間技術的發展而出現的一項新技術［1］。目前歐洲太空局［2 -3］、美國［4］、英國［5 -7］、日本［8 -9］以及國內的一些研究機構［10 -13］正在積極開展相關方面的研究。雖然關于空間繩網的公開資料十分有限，但是可知某些相關支撐技術（如空間繩系動力學、材料和釋放控制技術）已經通過了空間飛行試驗考核。對于繩網發射展開程序方法，目前所公布的技術資料中主要提及以下兩種模式：

1）發射準備前，繩網收納于可旋轉軸內部，4個頂點分別與質量塊相連接。動量輪加速中心轉軸及質量塊，在一定的旋轉速度下釋放質量塊，繩網在質量塊離心力的作用下實現旋轉展開，稱之為旋轉展開模式［6］。

2）發射準備前，繩網折疊收納于網艙內，4個頂點分別與質量塊相連接。發射器點火后，火藥推動質量塊以特定的角度、速度發射，繩網在質量塊的牽引下完成拋射過程，并逐步展開。繩網發射展開僅由一次發射即可完成繩網的拉出展開，稱之為一級發射模式［12 -16］。

目前旋轉展開模式在國外尚處在起步階段，技術相對復雜，對系統結構設計技術以及相關控制技術要求高，國內鮮有涉及。國內研究多采用一級發射模式，但在這種發射模式下，發射過程中網體接觸面積大、質量塊速度高，容易發生纏繞、穿透和打結等現象。

本文借鑒降落傘“先拉出、后展開”思想，針對空間繩網抓捕系統提出一種二級發射模式，并采用離散化的建模思路建立了系統的多體系統動力學模型，通過試驗對比驗證模型的有效性；對二級發射模式下的發射參數對繩網展開性能的影響進行了研究。

1 空間繩網二級發射模式

空間繩網的發射過程與降落傘的開傘過程具有一定相似性，但由于涉及穿透現象，問題更為復雜。降落傘的開傘過程按時序可分為拉直階段和充氣階段，通過按時序分階段控制提高了系統的可靠性和有效性，目前技術已經趨于成熟。本文借鑒降落傘的這種“先拉出后展開”思想提出了空間繩網的二級發射模式。

1. 1 系統組成

如圖1所示，空間繩網二級發射展開裝置由網艙、網艙蓋、一級發射裝置、二級發射裝置、質量塊（4個）組成。

1. 2 工作過程

二級展開模式下繩網的展開過程分為一級拉出和二級展開兩個過程。

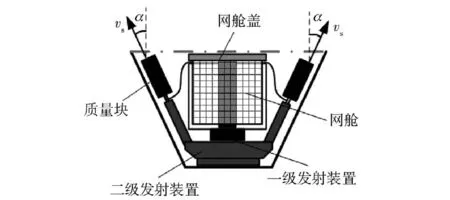
圖1 空間繩網二級發射裝置Fig. 1 Two-stage projection mechanism of space nets

空間繩網的一級拉出過程如圖2所示。網艙蓋在一級發射裝置的作用下獲得彈射速度υf，實現彈射分離。網包隨網艙蓋彈出，繩網在網艙蓋的帶動下從網包內依次“倒序”拉出。

圖2 一級拉出過程Fig. 2 The first-stage of outstretching course

空間繩網的二級展開過程如圖3所示。在繩網拉直到設定延時點火長度Ls瞬間，二級發射裝置點火推動4個質量塊按照設計發射速度υs、發射張角α運動（發射張角α定義為質量塊速度方向與網艙軸線間的夾角，如圖1所示）。在質量塊的牽引下，繩網由后向前逐步展開，并最終達到張滿狀態。

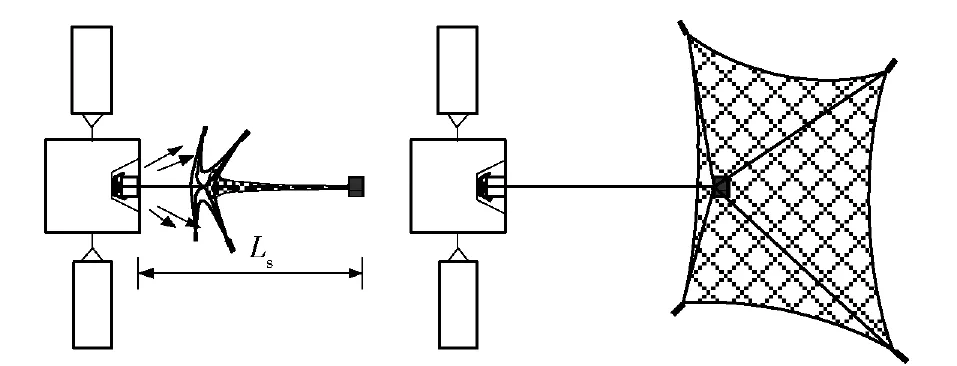
圖3 二級展開過程Fig. 3 The second stage of opening course

經過大量地面試驗驗證發現，無論是一級發射模式還是二級發射模式，繩網間的摩擦糾纏都無法完全避免，具有一定的不確定性。但二級發射模式將繩網拉出展開過程分離為拉出和展開兩個步驟，進行分步控制，保證了繩網規則、有序拉出，減弱了繩網拉出展開過程中的纏繞、穿透和打結等問題。

2 動力學模型

以集中質量阻尼彈簧方法［1，16］為基礎，在一定假設的前提下，建立空間繩網二級拉出模式的動力學模型。模型分為一級拉出模型和二級展開模型兩個部分。

2. 1 一級拉出模型

2. 1. 1 模型假設

在繩網一級拉出過程中，每一繩網束連續地從網包內拉出，未拉出的所有繩網固定在網包內，與網包和網艙蓋一起運動。為便于建立模型，進一步做如下假設：

1）網束從頂點到底端質量均勻增加；

2）網束拉出過程中，拉出中心點位置保持不變；

3）網束從網包內按序逐段拉出，不存在兩段或多段同時拉出，即不存在所謂突然“抖出”現象。

如圖4所示，在上述假設前提下，將已拉出的網束劃分為n個節點，n -1個繩段。每個繩段處理為質量集中在兩端節點上的阻尼彈簧，節點i的質量記為mi，連接節點i、j的繩段單元記為sij.

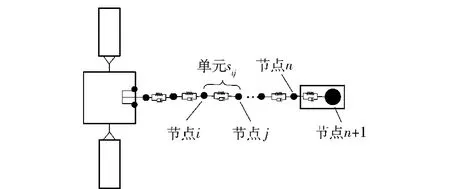
圖4 拉出過程的離散化模型Fig. 4 Discretization model of outstretching course

空間繩網系統簡化為由已拉出的網束單元sij、正在拉出的網束節點n以及網艙蓋節點n +1組成的多體系統。

2. 1. 2 已拉出節點動力學方程

已拉出繩段節點的運動由相應繩段上的繩索張力、氣動阻力和重力來決定。

繩段單元sij的繩索張力Tij近似為線彈性與線性阻尼之和，可由（1）式進行計算：

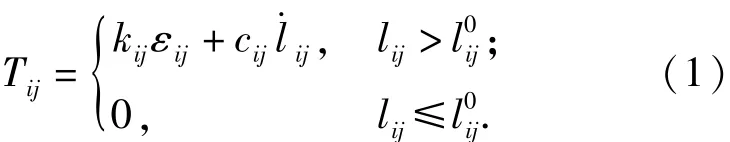
如圖5所示，在慣性系下節點i、j的位置矢量分別為r、r，則繩段s的實際長度l及其變化率為

ijijij

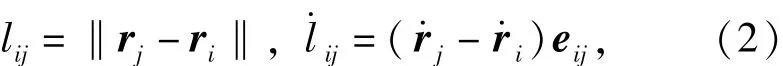
式中：eij為由節點i指向節點j的單位矢量，即

圖5 繩段單元質量阻尼彈簧模型Fig. 5 Semi-spring damper model of tether segment

繩段sij的等效彈性系數kij為

式中：E為楊氏模量，由材料屬性決定；Aij為繩段sij的橫截面積。

繩段sij的等效阻尼系數cij為

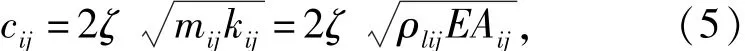
式中：mij為繩段sij的質量；ζ為繩索阻尼比，該參數取決于繩索的材料和編織方式。

作用于繩段的外力主要包括重力和氣動力，氣動力可以分解為氣動阻力和氣動升力，如圖6所示。作用于繩段sij的外力F為

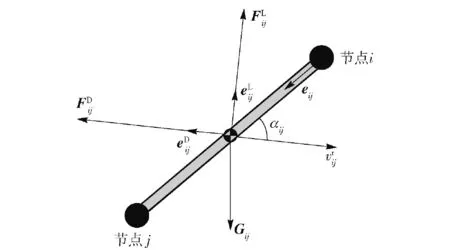
圖6 地面環境下作用于sij的外力Fig. 6 Aerodynamic force applying on cable

設地面重力加速度為g，方向豎直向下，則重力Gij可表示為

式中：ρlij為sij的線密度。

式中：ρair為大氣密度；dij為繩段的直徑；v為繩段相對于風的速度，設地面風速為vwind，則

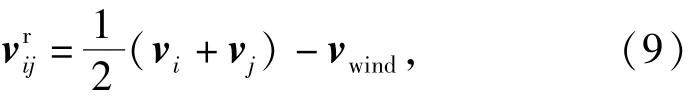
vi和vj分別為節點i和節點j的速度；e為氣動阻力方向單位矢量，與方向相反；e為氣動升力方向單位矢量，有

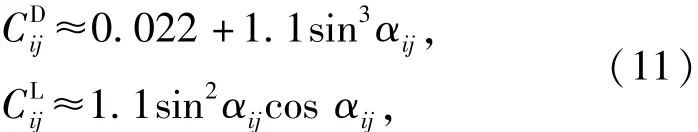
αij為sij的攻角。

定義conn｛i｝為共用節點i的所有單元的集合，在地心慣性系下，已拉出繩段節點i的動力學方程可以表示為

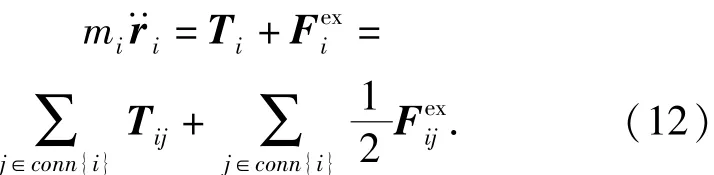
2. 1. 3 正在拉出繩網束結點的動力學方程

正在拉出的網束采用變質量動力學模型，以避免拉出過程中繩網束張力的劇烈波動。如圖4所示，在模型中認為正在拉出繩段的質量集中在第n個繩段結點上，即第n個結點是變質量點。則其動力學方程具有如下形式：

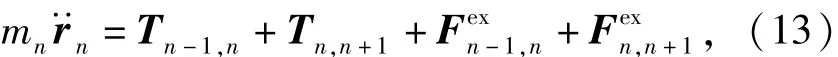
式中：Tn -1，n、F分別可有（1）式和（6）式求得；F可將（6）式～（8）式中的繩段自然長度替換為繩段拉出長度ln，n +1求得；Tn，n +1可根據動量守恒定律表示為

2. 1. 4 網艙蓋的動力學方程

在本模型中網艙蓋、網包以及未拉出的繩段一起運動，將其質量記為mn +1.則其動力學方程為

式中：vb為網艙蓋的速度；Qn +1為網艙蓋的氣動力。

聯立由（12）式、（13）式和（17）式得到空間繩網拉出過程中的多體系統動力學方程組。

初始時刻，所有繩網束節點及網艙蓋節點重合于坐標（0，0，0）點，網束第1節點與網艙固連，網艙蓋及網包內的繩網節點獲得非零常值初始速度v0b.對方程組進行數值求解即可得到空間繩網拉出過程中各節點的運動狀態。

2. 2 二級展開模型

如圖7所示，對于二級展開過程采用離散化的建模思路［12］，將繩索單元處理為質量阻尼彈簧單元，繩網則簡化為通過繩索單元連接的多體系統動力學模型。在建模過程中，首先計算各單元張力，再計算各單元所受外力，然后將其等效到關聯節點上；最后聯立各節點動力學方程，得到繩網系統的動力學方程。方程的初始邊界條件由一級拉出方程的計算結果映射得到。

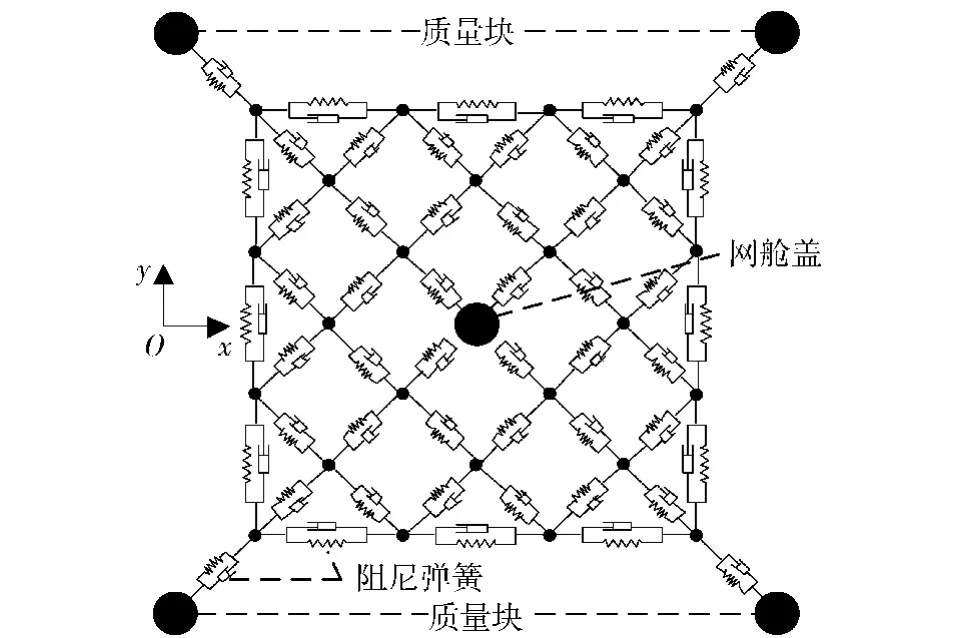
圖7 繩網多體系統示意圖Fig. 7 Multibody system model of flexible net

2.2.1 基本假設

繩網二級展開動力學模型的基本假設如下：

1）繩索可拉不可壓，有縱向的彈性和阻尼；

2）忽略繩索結構中的彎曲撓性。

2. 2. 2 網格離散

設L為繩網邊長，Nd為正方形繩網每條邊劃分的段數，Lmesh為網目尺寸，則對于四邊形菱型網，有

設N為繩網劃分的總節點數，則對于正方形網目的繩網，有

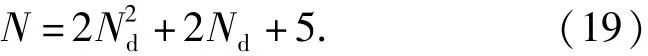
設Ns為繩網劃分的總繩段數，則對于正方形網目的繩網，有

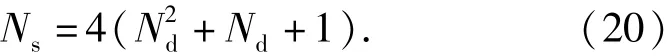
假設繩段的質量集中均分于兩端點，則節點的質量等于與之相鄰的繩段的質量之和的一半。節點i的質量mi為

另外，對于4個質量塊節點，還需在（21）式右側加上質量塊的質量ms.

2. 2. 3 系統節點動力學方程

節點內力為繩段中的張力，將繩段單元等效為“半彈簧阻尼”單元，繩段中的張力由（1）式計算得到。

節點外力包括重力和氣動力，分別由（7）式和（8）式計算得到。

求得節點內力和外力后得到系統動力學方程，具體形式見（12）式。

2. 2. 4 初始邊界條件傳遞

二級展開模型中各節點的初始位置和速度的x、y向分量由網格離散得到，z向分量由一級拉出模型的計算結果映射得到。

設由一級拉出過程結束時計算得到的網束節點位置和速度的z向分量分別為r和，二級展開模型中各節點的初始位置和速度的z向分量分別為r和，則在如圖8所示的映射點上滿足如下關系：

3 地面試驗與仿真

為驗證空間繩網二級拉出模式及其動力學模型，設計并開展了空間繩網地面試驗。試驗針對一級發射模式和二級發射模式分別建立了兩種試驗工況。

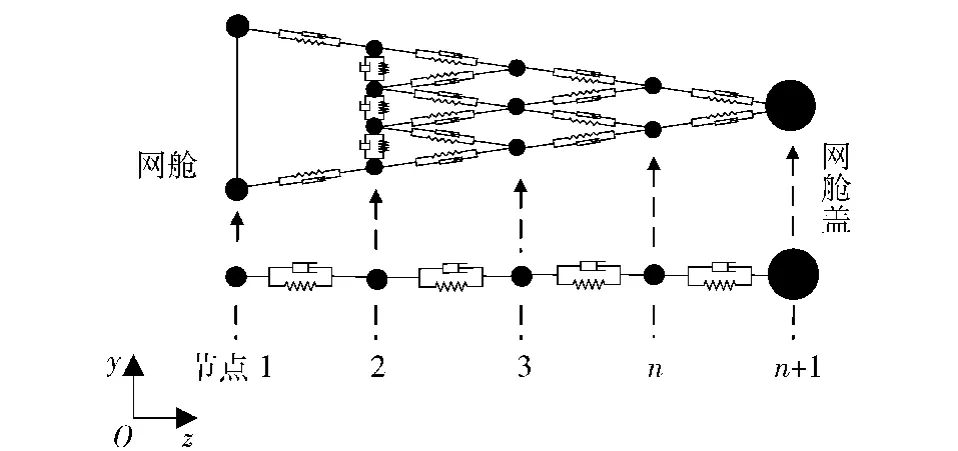
圖8 節點位移與速度信息的傳遞示意圖Fig. 8 Node displacement and transfer of velocity information

地面試驗采取垂直向下發射方式。繩網采用40 m×40 m正方形菱形網（繩網構型參考圖7），設計面積（平鋪狀態）為1 600 m2，網目邊長為0. 4 m.

繩網材料選取如表1所示。繩網質量為3.6 kg，網艙蓋質量為0. 5 kg，4個質量塊質量均為1. 5 kg.

表1 繩網材料Tab. 1 Material of space net

一級發射模式下，4個質量塊的發射速度為25 m/ s，發射張角為55°；二級發射模式下，一級發射速度υf=3 m/ s，延時點火長度Ls= 27 m，二級發射速度υs=25 m/ s，二級發射角度α=55°.

根據上述試驗工況，利用FORTRAN語言編程建立了空間繩網的兩種發射模式下的動力學模型，進行了仿真計算。

圖9所示為二級模式下繩網完成一級拉出后繼續進行二級展開的位型圖。

定義繩網的展開面積為飛網網口在發射方向的投影面積，描述了飛網的實際覆蓋范圍，決定了飛網可捕獲目標的尺寸。由于試驗數據僅跟蹤質量塊的運行軌跡，故采用簡化（23）式計算展開面積：

式中：r代表質量塊位移矢徑在垂直飛網發射方向上的投影；下標代表質量塊沿同一方向的順序編號。

定義繩網的飛行距離為飛網4個質量塊在飛網發射方向上的飛行距離，由（24）式計算：

圖9 空間繩網二級展開位型圖Fig. 9 The shape of space nets during deployment

式中：R代表質量塊位移矢徑在沿飛網發射方向上的投影距離；下標代表質量塊沿同一方向的順序編號。

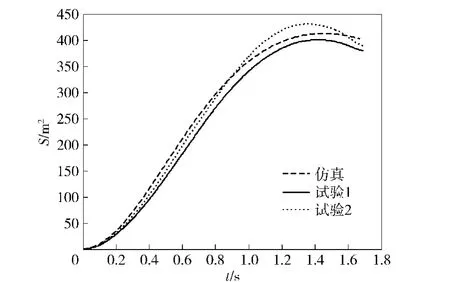
圖10 繩網展開面積仿真與試驗結果對比（二級發射模式）Fig. 10 Area of net during deployment（the two stage projection mode）

圖10和圖11分別給出了二級發射模式下繩網展開面積和飛行距離D的仿真結果與試驗結果對比曲線。雖然兩條試驗曲線試驗工況相同，但結果仍然存在一定的差值，說明繩網作為一個復雜的柔性系統具有一定的不確定性。盡管如此，仍可以看出在繩網拉出展開過程中繩網展開面積以及飛行距離的仿真結果與試驗結果具有較好的一致性。另外，由于空氣阻力及重力作用的影響，繩網展開面積遠小于繩網設計面積也是符合實際情況的。

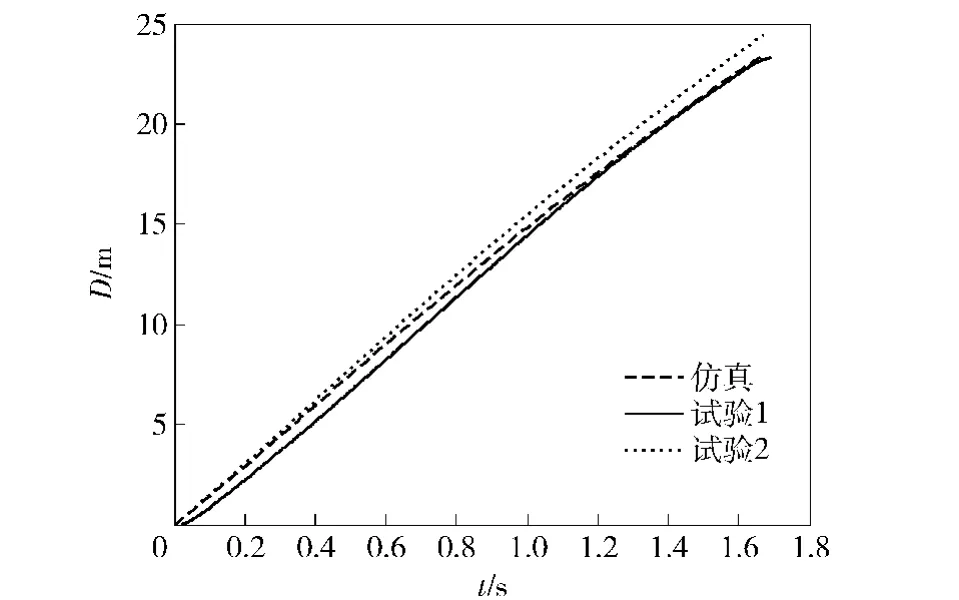
圖11 繩網飛行距離仿真與試驗結果對比（二級發射模式）Fig. 11 Flight distance of net during deployment （the two stage projection mode）

圖12和圖13分別給出了兩種發射模式下繩網展開面積和飛行距離的仿真結果，二級發射模式下繩網的最大展開面積以及飛行距離均明顯高于一級發射模式。與一級發射模式相比，二級發射模式在繩網展開性能方面具有明顯的優越性。

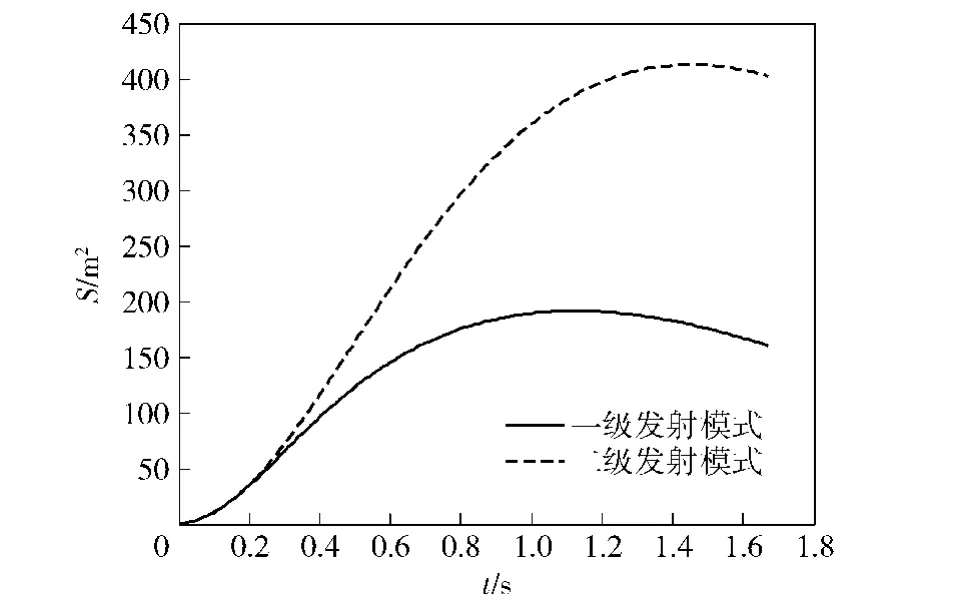
圖12 不同發射模式下的繩網展開面積Fig. 12 Extended area of net in different projection modes

在上述動力學模型基礎之上，繼續研究了繩網在太空環境下的最大展開面積與一級發射參數之間的影響關系。在太空環境下，忽略空氣阻力和重力的影響，固定二級發射速度為υs=25 m/ s，二級發射角度為α=55°，取一級發射速度υf和延時點火長度Ls分別為5 m/ s、6 m/ s、7 m/ s、8 m/ s、9 m/ s、10 m/ s、11 m/ s和2 m、7 m、12 m、17 m、22 m、27 m，得到如圖14的仿真結果。

從圖14可以看出：在選定參數范圍內，繩網最大展開面積隨一級點火長度Ls的增加先增大、后減小，隨一級發射速度υf的增大而增大。在（Ls= 7 m，υf= 11 m/ s）、（Ls= 12 m，υf= 11 m/ s）以及（Ls=12 m，υf= 10 m/ s）3種工況下已經達到了甚至超過了繩網設計面積（繩網存在一定的彈性）；但在（Ls=2 m，υf=5 m/ s）工況下，繩網的最大展開面積僅約為1 460 m2.

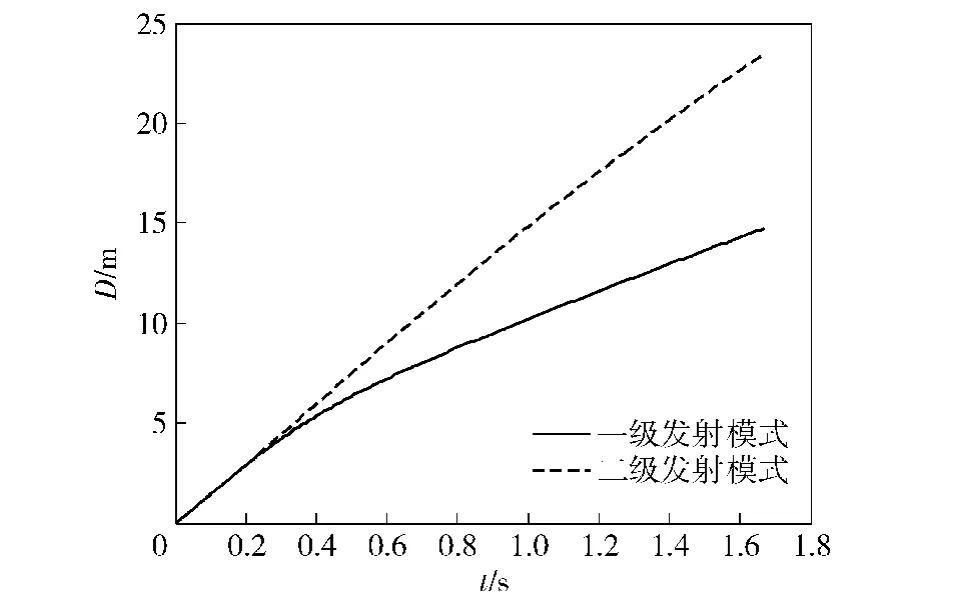
圖13 不同發射模式下的繩網飛行距離Fig. 13 Flight distance of net in different projection modes

圖14 繩網最大展開面積與延時點火長度關系Fig. 14 Max area vs length of projection delay

分析可知，由于消除了空氣阻力和重力的影響，繩網最大展開面積遠大于地面試驗情況，在參數合理的情況下可以達到完全展開。

在空間繩網二級發射模式下，繩網能否更好地達到設計面積與發射參數間的匹配關系有關。繩網中心點與網艙蓋（質量mf）相連，一級發射裝置點火使得繩網中心點獲得一定的初速度υf，二級發射裝置點火使得繩網4個角點質量塊（質量ms）獲得初速度υs，繩網中心點和角點速度的匹配情況直接影響繩網構型變化。當二者存在差值時，動量就會通過柔性繩網進行傳遞，重新分配。在這個交換的過程中伴隨有系統能量的衰減，以及繩網構型的變化。

仿真的結果表明：二級發射模式下，延時點火長度和一級發射速度等各項發射參數對空間繩網的展開性能影響較大，在仿真試驗工況范圍內，在（Ls=12 m，υf=11 m/ s）時，展開性能達到相對最優。通過加大仿真參數密度，可以獲得使展開性能達到最佳的精確發射參數組合。

4 結論

空間繩網是一種具有潛在應用價值的新型空間結構。本文提出空間繩網的二級發射模式，并進行了動力學建模與分析，初步得到以下結論：

1）空間繩網二級發射模式有助于避免繩網展開過程中出現的纏繞打結問題，具有可行性，是空間繩網發射模式的一種新思路。

2）仿真結果與試驗數據基本吻合，數值仿真模型有效，可以作為空間繩網發射優化設計的參考依據。

3）在給定發射參數范圍內，可以使用文中所建立的仿真程序計算得到最優發射參數組合，使得繩網展開性能最佳。

參考文獻（References）

［1］ 劉海濤.空間繩網展開及復合體離軌動力學與控制［D］.長沙：國防科學技術大學，2014. LIU Hai-tao. Dynamics and control of space net deployment and combination reorbiting［D］. Changsha：National University of Defense Technology，2014.（in Chinese）

［2］ Sinn T，McRobb M，Wujek A. Results of REXUS12s suaineadh experiment deployment of a spinning space web in micro gravity conditions［C］∥63rd International Astronautical. Congress. Naples，Italy：The Suaineadh Team，2012.

［3］ Mankala K K，Agrawal S K. Dynamic modeling and simulation of impact in tether net/ gripper systems［J］. Multibody System Dynamics，2004，11（3）：235 -250.

［4］ Summerer L，Purcell O，Vasile M，et al. Making the first steps towards solar power from space-microgravity experiments testing the deployment of large antennas［C］∥60th International Astronautical Congress. Daejeon，Korea：International Astronautical Federation，2009.

［5］ G?rdsback M，Tibert G. Optimal deployment control of spinning space webs and membranes［J］. Journal of Guidance，Control，and Dynamics，2009，32（5）：1519 -1530.

［6］ G?rdsback M，Tibert G. Deployment control of spinning space webs［J］. Journal of Guidance，Control，and Dynamics，2009，32（1）：40 -50.

［7］ Palmerini G B，Sgubini S，Sabatini M. Space webs based on rotating tethered formations［J］. Acta Astronautica，2009，65（1/2）：131 -145.

［8］ Sakamoto H，Natori M C，Kadonishi S，et al. Folding patterns of planar gossamer space structures consisting of membranes and booms［J］. Acta Astronautica，2014，94（1）：34 -41.

［9］ Haraguchi D，Sakamoto H，Shirasawa Y，et al. Design criteria for spin deployment of gossamer structures considering nutation dynamics［C］∥AIAA Guidance，Navigation，and Control Conference. Toronto，Canada：American Institute of Aeronautics and Astronautics，2010.

［10］ 王波，郭吉豐.采用超聲波電機的空間飛網自適應收口機構設計［J］.宇航學報，2013，34（3）：308 -313. WANG Bo，GUO Ji-feng. Design of self-adaptative take-up mechanism for space net using ultrasonic motor［J］. Journal of Astronautics，2013，34（3）：308 -313.（in Chinese）

［11］ 劉海濤，張青斌，楊樂平，等.空間繩網系統展開動力學特性分析［J］.國防科技大學學報，2015，37（3）：68 -77. LIU Hai-tao，ZHANG Qing-bin，YANG Le-ping，et al. The deployment dynamic characteristics analysis of space web system ［J］. Journal of National University of Defense Technology，2015，37（3）：68 -77.（in Chinese）

［12］ 張青斌，孫國鵬，豐志偉，等.柔性繩網動力學建模與天地差異性分析［J］.宇航學報，2014，35（8）：871 -877. ZHANG Qing-bin，SUN Guo-peng，FENG Zhi-wei，et al. Dynamic modeling and difference analysis between space and ground for flexible nets［J］. Journal of Astronautics，2014，35（8）：871 -877.（in Chinese）

［13］ Zhai G，Zhang J R，Zhang Y. Circular orbit target capture using space tether-net system［J］. Mathematical Problems in Engineering，2013，2013（4）：1 -11.

［14］ 高智杰，孫富春，閔海波，等.飛網拋射過程母衛星姿態干擾分析與姿態控制［J］.力學學報，2013，45（3）：434 -441. GAO Zhi-jie，SUN Fu-chun，MIN Hai-bo，et al. Study on attitude disturbance and control of mother satellite during space net projecting［J］. Chinese Journal of Theoretical and Applied Mechanics，2013，45（3）：434 -441.（in Chinese）

［15］ 王波，郭吉豐.空間飛網質量塊動力學分析及收口機構優化設計［J］.宇航學報，2012，33（10）：1377 -1383. WANG Bo，GUO Ji-feng. Dynamics analysis of mass block and optimization design of take-up mechanism for space net［J］. Journal of Astronautics，2012，33（10）：1377 -1383.（in Chinese）

［16］ 陳欽，楊樂平，張青斌.空間飛網發射動力學建模仿真研究與地面試驗［J］.國防科技大學學報，2009，31（3）：16 -19. CHEN Qing，YANG Le-ping，ZHANG Qing-bin. Dynamic model and simulation of orbital net casting and ground test［J］. Journal of National University of Defense Technology，2009，31（3）：16 -19.（in Chinese）

Dynamics Analysis of a Two-stage Projection Scheme of Space Nets System

GAO Qing-yu，TANG Qian-gang，ZHANG Qing-bin，FENG Zhi-wei
（College of Aerospace Science and Engineering，National University of Defense Technology，Changsha 410073，Hunan，China）

Abstract：A two-stage projection scheme of space nets is proposed by using“outstretching first and opening later”idea in parachute inflation process，and a numerical simulation model is developed. In the proposed scheme，the projection process of space nets is divided into two successive courses：the first-stage of outstretching course and the second-stage of opening course，through which the process is controlled step by step to pull out the space nets regularly and ordinarily，and avoid their twining，penetration and knotting problems. Through a contrastive analysis of the numerical simulation result and the experiment result，the numerical simulation model is tested and verified. The two-stage projection scheme of space nets and the numerical simulation model developed in this paper provide a reference way to carry out optimization design of space nets.

Key words：aircraft launch and recovery，flight technology；space net；dynamic modeling；two-stage projection；numerical simulation；optimization design

中圖分類號：V423

文獻標志碼：A

文章編號：1000-1093（2016）04-0719-08

DOI：10. 3969/ j. issn. 1000-1093. 2016. 04. 021

收稿日期：2015-06-16

基金項目：國家自然科學基金項目（11272345）

作者簡介：唐乾剛（1958—），男，教授，博士生導師。E-mail：kdtqg@ sina. com；