基于貝葉斯網絡的機載氧氣系統(tǒng)可靠性評估

王　鵬，陳　曦，閻　芳，趙長嘯

（中國民航大學a.天津市民用航空器適航與維修重點實驗室；b.中歐航空工程師學院，天津　300300）

?

基于貝葉斯網絡的機載氧氣系統(tǒng)可靠性評估

王鵬a，陳曦b，閻芳a，趙長嘯a

（中國民航大學a.天津市民用航空器適航與維修重點實驗室；b.中歐航空工程師學院，天津300300）

摘要：通過分析機載氧氣系統(tǒng)架構，構建基于貝葉斯網絡的系統(tǒng)可靠性評估模型。通過前向和后向推理得到葉節(jié)點失效率及根節(jié)點后驗失效概率，結合重要度及聯合重要度的大小，找出影響系統(tǒng)可靠性的關鍵因素，求解最大可能解釋（MPE）。通過與故障樹分析（FTA）法對比，說明該方法的優(yōu)勢。綜合各定量分析結果，說明貝葉斯網絡方法進行可靠性評估的有效性，評估結果還可對系統(tǒng)結構設計和故障診斷提供相關參考信息。

關鍵詞：貝葉斯網絡；機載氧氣系統(tǒng)；定量評估

飛機系統(tǒng)安全性分析常采用故障樹分析法（FTA），對于設定的頂事件，該方法采用自上而下的方法，逐步找出引發(fā)故障的底事件。通過對頂事件失效率以及相關的定性和定量結果，考慮設計是否滿足安全性要求。利用故障樹中的邏輯符號可清晰地表示出各事件間的邏輯關系。在進行定性和定量評估前，還需求出故障樹最小割集，當所研究系統(tǒng)高度復雜時，會存在很多基本事件，生成大量最小割集，為解決組合爆炸問題，還需采取近似和截斷方法。現有的近似和截斷方法都僅適用于二態(tài)單調系統(tǒng)，對多態(tài)、非單調系統(tǒng)無能為力［1］。此外文獻指出FTA在應用上的限制：當系統(tǒng)存在多個失效狀態(tài)，那么對于其中的每一個可要求構建單獨的故障樹，這會增加評估工作量［2］。

貝葉斯網絡是基于概率理論和圖論的一種方法，最早由Pearl于1986年提出。通過利用概率推算，貝葉斯網絡可進行正向和反向的推理，處理系統(tǒng)多狀態(tài)以及不確定性問題［3］，這些是用故障樹方法無法完成的。在高效的推理算法和成熟軟件支持下，在可靠性和安全性評估領域得到越來越多的關注及應用。貝葉斯網絡已成功用于多領域，如電網可靠性評估、醫(yī)學診斷、數據挖掘和智能決策等。應用貝葉斯網絡進行系統(tǒng)評估和分析，可避免求解系統(tǒng)的最小割集，使分析更加直觀并減少計算量。在已建立故障樹情況下，可直接將其映射轉化成貝葉斯網絡［4］。

1　評估模型構建

1.1氧氣系統(tǒng)架構分析

飛機的氧氣系統(tǒng)由3個子系統(tǒng)組成：空勤氧氣系統(tǒng)、旅客氧氣系統(tǒng)和便攜式氧氣設備。通過介紹旅客氧氣系統(tǒng)控制原理，以“旅客氧氣面罩自動、手動拋放控制系統(tǒng)都失效”為頂事件進行可靠性評估分析。

旅客氧氣系統(tǒng)由旅客氧氣裝置和控制拋放電路組成。其裝置采用化學氧，控制拋放電路主要由自動拋放信號源（IASC）、高度繼電器、手動拋放按鈕、拋放繼電器和旅客氧氣狀態(tài)繼電器等組成，圖1給出該控制系統(tǒng)的原理圖。當座艙高度超過4 200 m時，IASC為旅客氧氣控制系統(tǒng)輸出接地信號，通過繼電器控制實現面罩的拋放，并將狀態(tài)信息傳送給燈式開關和告警系統(tǒng)。另一方面，空勤人員可通過按下駕駛艙內的“PASS OXY ON”，通過繼電器控制來實現手動拋放。其中自動和手動拋放控制方式是獨立工作的，手動拋放的設計作為冗余設計，可以有效地提高系統(tǒng)可靠性和安全性。該系統(tǒng)控制電路采用的是右28 V直流供電通道供電，并且有左應急直流供電通道作為備用通道。

圖1　旅客氧氣系統(tǒng)控制原理圖Fig.1　Schematic diagram of passenger oxygen control system

1.2貝葉斯網絡構建

具有N個節(jié)點的貝葉斯網絡可用BNN=＜＜V，E＞，P＞表示，＜V，E＞表示有向無環(huán)圖，V =｛V1，…，VN｝表示節(jié)點集合，有向邊E代表變量間的依賴關系。對于有向邊（Vi，Vj），Vi稱為Vj的父節(jié)點，Vj稱為Vi的子節(jié)點。沒有父節(jié)點的節(jié)點稱為根節(jié)點，沒有子節(jié)點的節(jié)點稱為葉節(jié)點［5］。

P表示節(jié)點條件概率分布（condition probability distribution）。它以概率為基礎，定量刻畫父子節(jié)點間的依賴關系，其中根節(jié)點對應的是先驗概率分布。

在分析旅客氧氣控制系統(tǒng)構架的基礎上，構建貝葉斯網絡模型用于可靠性分析。一般來說，在知道系統(tǒng)架構的基礎上，利用已有的因果關系來確定貝葉斯網絡的結構，尤其針對大規(guī)模復雜網絡，可有效提高建模效率及準確性。

構建的貝葉斯網絡模型如圖2所示，表1給出各節(jié)點的實際含義。在該網絡中，根節(jié)點與故障樹中的底事件相對應，中間節(jié)點與中間事件相對應，葉節(jié)點則對應頂事件，有向邊體現了節(jié)點的因果相關性。D節(jié)點到A節(jié)點的有向通路有2條，因此該網絡是多連通的網絡。

網絡中同時存在從D到C和到B的有向邊，說明節(jié)點D是節(jié)點C和B的父節(jié)點，在故障樹方法中，D對應的事件則要出現2次。對于這種產生多重影響的事件，在構建故障樹時每次都需要表示，這會使結構顯得復雜，而在貝葉斯網絡中，只需一個節(jié)點和多個有向邊即可表示這種多重相關性。貝葉斯網絡因為缺少邏輯符號使得邏輯關系顯得不直觀，雖然在定性分析方面不具優(yōu)勢，但在定量分析上卻體現了很多優(yōu)點。

確定貝葉斯網絡的拓撲結構后，還需考慮中間節(jié)點的條件概率分布以及根節(jié)點先驗概率分布，分別對應于系統(tǒng)不同層級的邏輯關系和底事件的先驗可靠性信息。本文氧氣系統(tǒng)的分析基于二態(tài)系統(tǒng)，即每個節(jié)點只有失效和正常2種狀態(tài)，并體現確定的邏輯關系：其中用f表示失效狀態(tài)，t表示正常工作狀態(tài)。

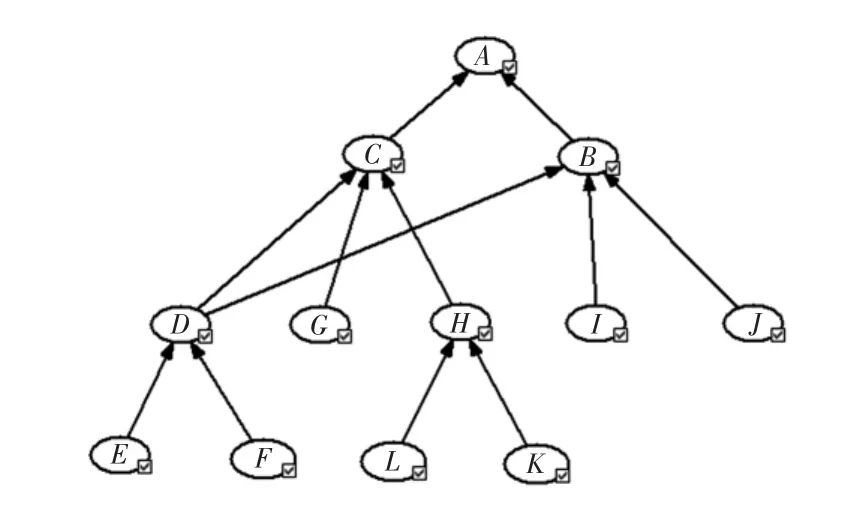
圖2　用于氧氣系統(tǒng)評估的貝葉斯網絡Fig.2　Bayesian network used for oxygen system assessment

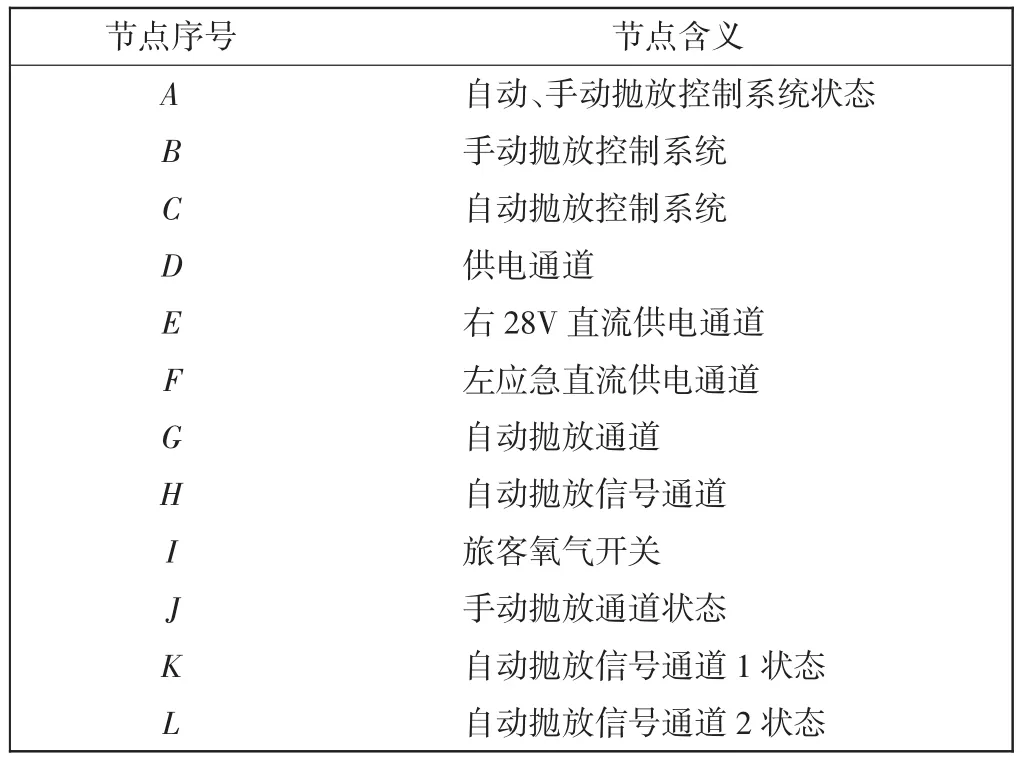
表1　網絡中各節(jié)點含義Tab.1　Meaning of network nodes

故障樹中常用邏輯門都可用貝葉斯網絡體現，這種關系體現在節(jié)點的條件概率表（condition probability table）中。限于篇幅原因，本文僅給出C和D節(jié)點所對應的條件概率表（CPT），如表2所示。2個CPT分別對應或門和與門關系。

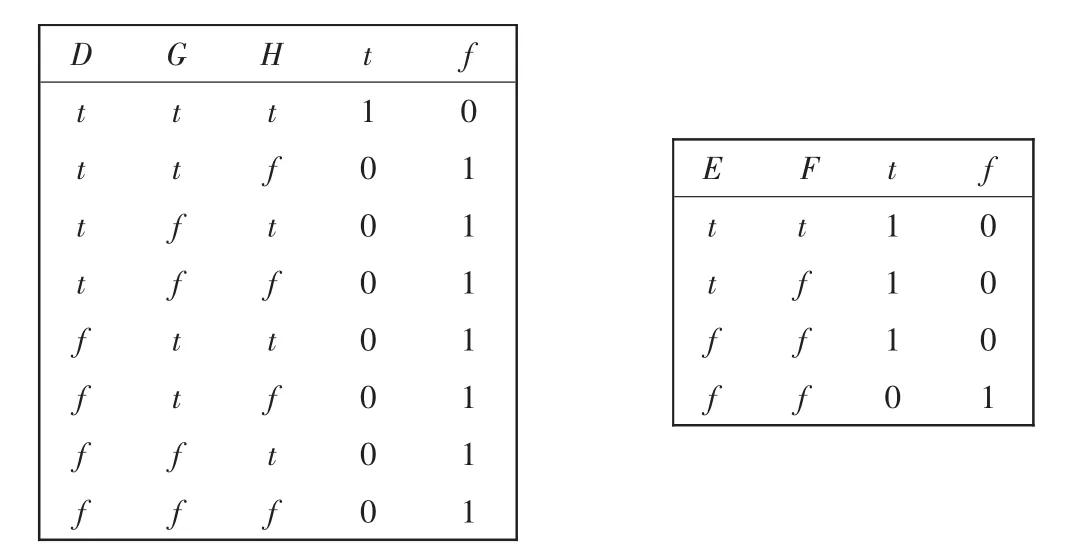
表2　節(jié)點C和D的條件概率表Tab.2　Condition probability of node C and node D

對于根節(jié)點，通過FMEA（失效模式和影響分析）可得到對應節(jié)點的失效率，在此基礎上給出節(jié)點先驗概率分布，如表3所示。

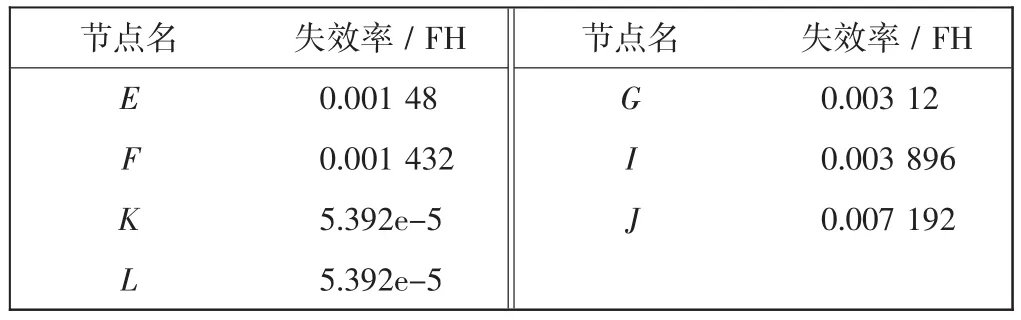
表3　根節(jié)點對應底事件的失效率Tab.3　Failure rate of primary events by root nodes

2　系統(tǒng)可靠性評估

2.1貝葉斯網絡的推理

貝葉斯網絡的推理，又稱為信度更新（belief updating），其過程基于概率論理論。直接使用聯合分布進行推理的復雜度相對于變量個數成指數增長，一般來說，對N個二態(tài)變量的聯合概率分布會包含2n- 1個獨立參數［6］，變量數量較多時，聯合概率的獲取和運算都很困難。

利用變量間的條件獨立關系，可將聯合概率分布分解成如下的乘積形式

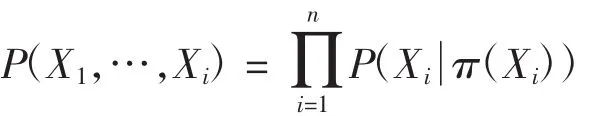
其中：π（X）i表示節(jié)點Xi的父節(jié)點，當π（X）i不存在時，P（π（X）i）為邊緣分布P（X）i。通過分解聯合概率可使復雜度降低，進而提高推理效率。

貝葉斯網絡的推理算法分為精確推理和近似推理。2種算法均被指出是NP問題。在這些算法中，消息傳遞算法只適用于單連通網絡，其他算法對單、多連通網絡都適用。其中聯結樹算法（junction tree algorithm）由Lauritzen等［8］于1988年提出，該算法分為2種：Shafer-Shenoy算法和Hugin算法。Park和Darwiche結合這2種算法的優(yōu)點，對聯結樹算法進行了改進，大大提高了算法效率［9］。聯結樹算法計算速度最快并且準確，很多貝葉斯網絡應用軟件都將其作為默認或可選推理算法。

經計算得到葉節(jié)點A失效率為3.66×10-5，體現了頂事件的失效率，利用故障樹也可得到。但由于利用貝葉斯網絡可進行雙向推理，在推理過程中加入證據，還可得到故障樹無法分析的結果。雙向推理依據的是貝葉斯定理，其描述了先驗及后驗概率間的關系

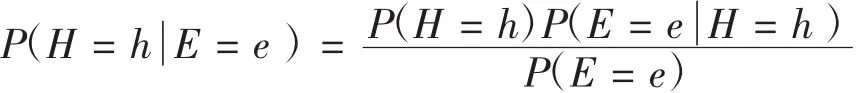
對于H和E為2個隨機變量，對事件H=h的概率P（H=h）稱為先驗概率。而在考慮證據E=e之后，對H=h的估計P（H=E=e）稱為后驗概率。根據此定理可得到底事件的后驗概率，假設給定證據A=f，得到的根節(jié)點后驗概率如表4所示，這種從結果考慮原因的過程叫做診斷推理。

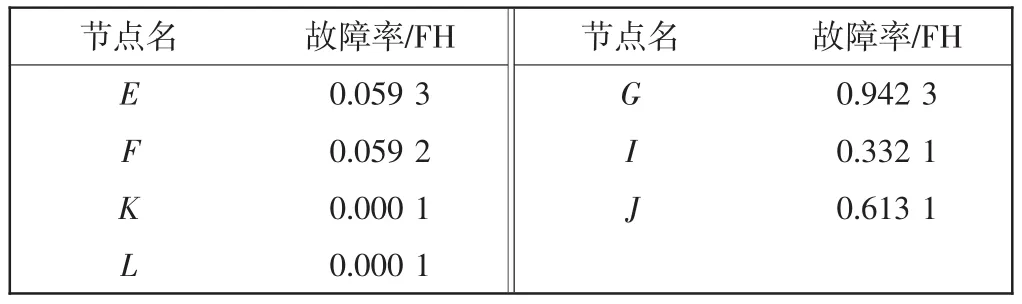
表4　根節(jié)點對應底事件的后驗失效率Tab.4　Posteriori failure rate of primary events by root nodes

2.2重要度分析

重要度分析的目的在于通過單一部件或幾個部件對系統(tǒng)整體可靠性影響的程度，識別系統(tǒng)可靠性薄弱環(huán)節(jié)。常用的重要度定義如下［10］：

Birnbaum Measure（BM）重要度，也叫概率重要度。其反映了某一元件在確定失效后和確定正常時系統(tǒng)失效率的變化，其數學表達式為

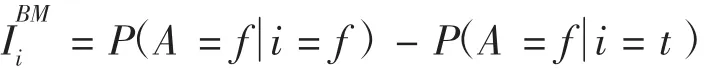
關鍵重要度，也叫臨界重要度，反映了某個元件失效概率的變化率所引起的系統(tǒng)失效概率的變化率。其數學表達式為

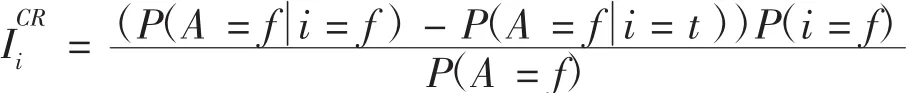
對根節(jié)點進行重要度計算，其結果如圖3所示，利用圖3可很直觀地比較各個重要度的大小。2種重要度分析中，前3項均為G、I、J、K和L的重要度遠小于其他項，表明其可靠性比其他節(jié)點的要高。

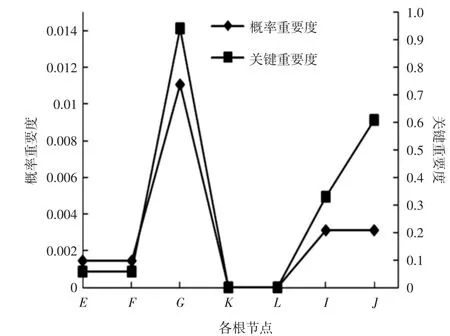
圖3　根節(jié)點重要度大小比較Fig.3　Importance comparison of root nodes

傳統(tǒng)重要度分析的是單一部件對系統(tǒng)可靠度的影響程度，J.S.Hong在概率重要度的基礎上提出了聯合概率重要度，目的是判斷系統(tǒng)中任意兩個部件失效發(fā)生時導致對系統(tǒng)可靠度的影響程度。但是此聯合重要度的取值區(qū)間從概率重要度取值區(qū)間［0，1］變?yōu)椋?1，1］，與系統(tǒng)的結構和失效模式對比存在很大差異。畢衛(wèi)星等［11］在此基礎上提出新的算法，并通過實例說明算法的有效性，該算法還可擴展到K個部件的情況，下面利用該新定義對系統(tǒng)進行分析。

對于i和j兩節(jié)點，聯合概率重要度的公式為

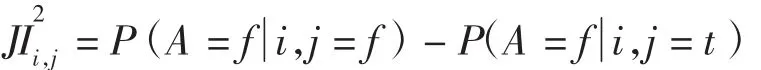
所有根節(jié)點的聯合關鍵重要度組合如表5所示。

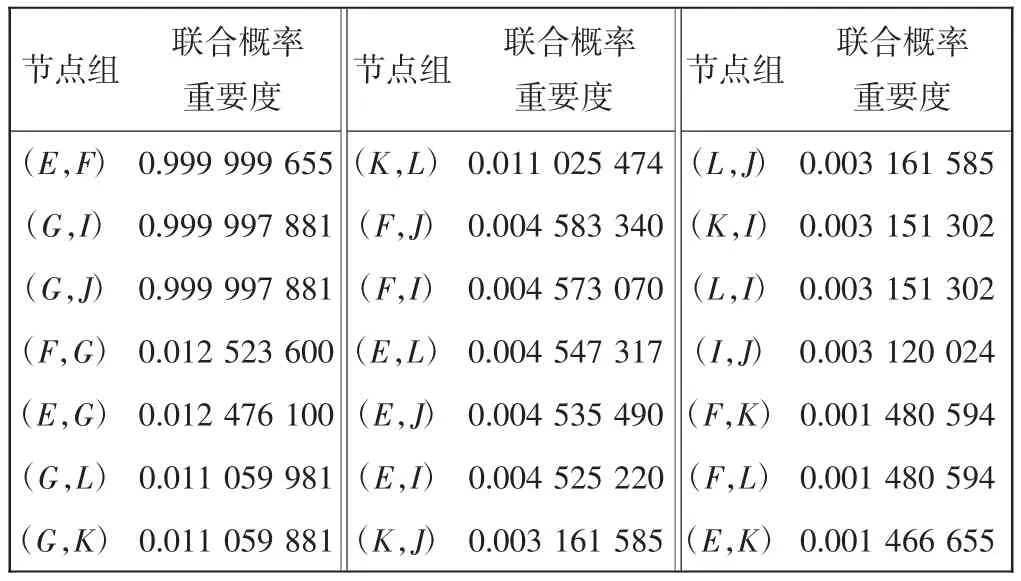
表5　聯合概率重要度結果Tab.5　Result of joint probability importance

對于該系統(tǒng)，手動拋放通道和旅客氧氣開關對應是最大的兩個失效概率，對聯合重要度結果進行分析，會發(fā)現兩者（I，J）的聯合重要度大小卻并不靠前，而失效率相對不大的E和F，聯合概率重要度卻排在了第1位。原因在于兩者雖然失效率不是最大，但當右28 V直流供電通道和左應急直流通道同時失效時，會引起自動和手動拋放同時失效，A的狀態(tài)變?yōu)閒，而手動拋放通道和旅客氧氣開關同時失效時，只會引起手動拋放失效，并不能引起A失效。

上述重要度可解決原聯合概率重要度取值出現負值的問題，但是并未考慮部件自身可靠性因素，在此基礎上作出進一步改進，提出了聯合關鍵重要度，兼容了部件本身可靠性因素，可以證明其值域也是［0，1］。其定義為

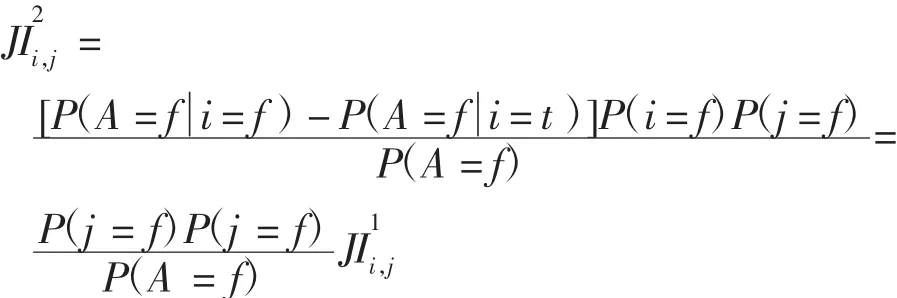
計算結果如表6所示。此時（E，F）的重要度有所下降，（I，J）的重要度提高到第4位，結合先驗失效概率可知這是由于E、F相對G、I、J的失效率較小導致的。綜合以上2種重要度結果，得到重要度前3的組合為（E，F）、（G，I）和（G，J）。

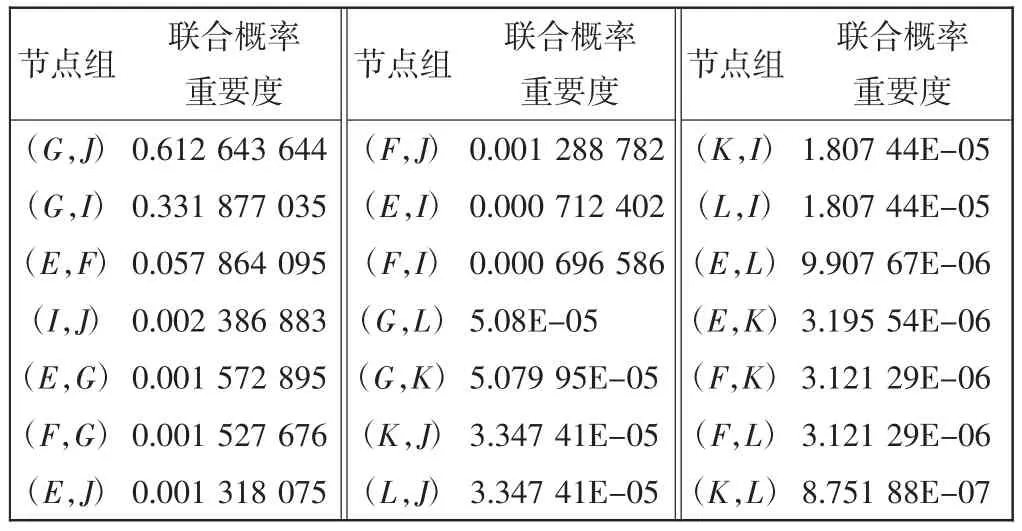
表6　聯合關鍵重要度結果Tab.6　Result of joint critical importance

2.3最大可能解釋

貝葉斯網絡推理不僅可以處理后驗概率問題，還可以求解最大后驗概率問題（maximum a posteriori hypothesis，MAP）以及最大可能解釋問題（most probable explanation，MPE）。MAP是為了找到相關變量的后驗概率最大的組合狀態(tài)，將這些相關變量稱為假設變量（hypothesis variables），記作H，H的一個狀態(tài)組合作為一個假設，記為h，給定證據E=e，找出所有假設中后驗概率最大的h*，即h*= argP（H =E = e），這就是最大后驗假設問題。當假設變量H包含所有非證據變量，MAP就變?yōu)镸PE問題，對應的h稱為解釋。

在本文舉例中，分析自動、手動拋放功能失效的MPE，則對應的證據變量及其狀態(tài)是｛A = f｝，對它的一個解釋為｛B，C，D，E，F，G，H，I，J，K，L = t｝，這樣的解釋組合最多共有211= 2 048個，利用Netica軟件的MPE功能可以直接求解。結果為

｛B，C，G，J = f，D，E，F，H，I，K，L = t｝

MPE的結果說明當面罩自動、手動拋放功能都失效時，最有可能由G和J失效引起。此結果與聯合關鍵重要度結果一致，并且對于故障診斷也有重要參考意義。

3　結語

采用貝葉斯網絡構建機載氧氣系統(tǒng)評估模型，對其進行了可靠性評估分析，并得出如下結論：

1）貝葉斯網絡在模型的表達上比故障樹清晰直觀，并且可避免求最小割集，進行精確的推理計算。

2）利用貝葉斯網絡不僅可以得到頂事件失效率（分析系統(tǒng)的可靠度）、重要度等結果，還可以在給定證據條件下推理，進行診斷分析，作出最大后驗解釋。

3）利用各個部件重要度、聯合重要度的分析以及診斷推理的結果進行綜合分析，找出了可靠性相對薄弱的G、I和J對應的部件，并且發(fā)現E和F同時失效會對系統(tǒng)可靠性產生嚴重影響。

參考文獻:

［1］EPSTAIN S，RAUZY A. Can we trust PRA［J］. Reliability Engineer and System Safety，2005，88（3）: 195-205.

［2］SAE. SAE ARP 4761 Guideline and Methods for Conducting the Safety Assessment Process on Civil Airborne System and Equipment［S］. SAE，1996.

［3］周忠寶，董豆豆，周經綸.貝葉斯網絡在可靠性分析中的應用［J］.系統(tǒng)工程理論與實踐，2006，26（6）：95-100.

［4］BOBBIO A，PORTINALE L，MINICHINO M，et al. Improving the analysis of dependable systems by mapping fault trees into Bayesian networks［J］. Reliability Engineer and System Safety，2001，71（3）: 249-260.

［5］張連文，郭海鵬.貝葉斯網引論［M］.北京：科學出版社，2006.

［6］王宏川.因果圖推理及其應用研究［D］.重慶：重慶大學，2002.

［7］厲海濤，金光，周經倫，等.貝葉斯網絡推理算法綜述［J］.系統(tǒng)工程與電子技術，2008，30（5）：935-939.

［8］LAURITZEN S L，SPIEGELHALTER D J. Local computations with probabilities on graphical structures and their applications to expert systems［J］. Journal of the Royal Statistical Society，1988，50（2）: 157-224.

［9］PARK J D，DARWICHE A. Morphing the Hugin and Shenoy-Shafer Architectures［C］//European Conference on Symbolic and Quantitative Approaches to Reasoning with Uncertainty，Aalborg，Danemark，2003: 149-160.

［10］尹曉偉，錢文學，謝里陽.系統(tǒng)可靠性的貝葉斯網絡評估方法［J］.航空學報，2008，29（6）：1482-1489.

［11］畢衛(wèi)星，陳建軍.一種改良的聯合重要度算法［J］.大連交通大學學報，2009，30（5）：74-76.

（責任編輯：黃月）

Reliability assessment of airborne oxygen system based on Bayesian network

WANG Penga，CHEN Xib，YAN Fanga，ZHAO Changxiaoa
（a. Civil Aircraft Airworthiness and Maintenance Key Lab of Tianjin；b. Sino-European Institute of Aviation Engineering，CAUC，Tianjin 300300，China）

Abstract:By analyzing airborne oxygen system architecture，the system reliability assessment model is built based on Bayesian network. The failure rate of leaf node and posteriori failure probability of root nodes are obtained by the forward and backward inferences，the key factors of system reliability are identified based on importance sequence and joint importance，the most probable explanation（MPE）is given. The advantages of the method are explained by comparing with FTA. Quantitative analysis proves the effectiveness of reliability assessment by using Bayesian network，and assessment results can also provide referencial information for the system structure design and fault diagnosis.

Key words:Bayesian network；airborne oxygen system；quantitative assessment

中圖分類號：V240.2

文獻標志碼：A

文章編號：1674－5590（2016）02－0001－05

收稿日期：2015-03-01；修回日期：2015-03-29基金項目：國家自然科學基金項目（U1333120）；國家重點基礎研究發(fā)展計劃（973計劃）（2014CB744902）

作者簡介：王鵬（1982—），男，天津人，副研究員，碩士，研究方向為民機系統(tǒng)安全性設計與評估、機載電子硬件適航技術.