中考反比例函數常見題型分析
黃志龍
摘 要: 反比例函數為初中函數重要內容,也是中考試卷中的必考題,其題型類型較多,學生掌握起來難度較大.為加深學生及教師對這一考點的理解與認知,作者結合歷年考試內容,對中考反比例函數題型展開分析,總結其知識點.
關鍵詞: 中考 反比例函數 題型分析函數屬于初中數學重要的學習內容,其中反比例函數屬于函數內容中的重要分支之一,同時也屬于中考考試熱點.反比例函數是對現實問題中涉及的數量關系加以刻畫的數學基礎模型,學生在學習這一章節內容時,在理解上容易出現偏差,部分學生對題型的把握并不準確.其實中考中涉及的反比例函數均可于課本習題中找到原型.課本習題實際是諸多專家通過反復篩選給出的具有延展性、代表性的題目,因此中學生應重視課本這一學習資料,掌握課本習題中反比例函數的提醒,以不變應萬變,將掌握的解題方法用于中考反比例函數的考試中.下文筆者結合課本上的練習題,分析中考中反比例函數常見題型.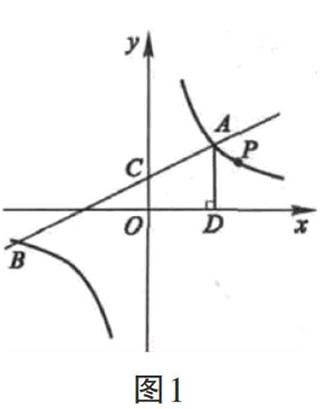
1.反比例函數和一次函數結合
中考中反比例函數和一次函數結合的這種題型比較多見,通過查閱近兩年中考題,我們可發現,每個省的中考題中均會有這一題型的相關考題出現.這一類的考題可在中學課本中找到原型,具體如下:
練習題一:正比例函數y=x圖像和反比例函數y=k/x的圖像有一個交點,縱坐標為2,求:(1)當x=-3時,反比例函數y的值;(2)當-3 分析:從本題已知信息中可以看出,兩個函數圖像有一個交點,其坐標是(2,2),由此可知反比例函數k為4.在解析(1)時,將x=-3帶入到反比例函數中,經解析可得y=-4/3.第(2)題在解析時,只需代入x=-1至反比例函數,可得y=-4,由此獲知y的取值范圍為-4 在中考中,反比例函數與一次函數結合的中考題考查的內容包括以下幾點:待定系數法求解析式;求三角形面積、對函數值大小進行比較、求取函數值或自變量取值范圍,等等. 我們對中考題進行分析,看怎樣利用上述思路解決中考中的相關反比例函數問題. 例題1(2011年河南卷):如圖1所示,一次函數y=kx+2和反比例函數y=k/x圖像,兩圖像在A(4,m)、B(-8,-2)處相交,和y軸交于C點.求解:(1)k與k的值;(2)根據函數圖像分析,若y>y,則x的取值范圍是多少?(3)過點A作AD與X軸在點D垂直,點P為反比例函數第一象限內圖像中的一點,假設直線OP和線段AD在點E相交,若S∶S=3∶1,點P坐標是多少? 解析:第(1)題的答案是1/2,16;第(2)題答案或x>4或-8 因為S∶S=3∶1,所以S=1/3×12=4.故而OD·DE為4,DE為2,可得點E坐標(4,2).由于點E位于直線OP之上,故OP解析式為y=1/2x,可得OP和y=16/x圖像于第一象限內交點P坐標是(4,2). 2.反比例函數增減性分析 練習題二:如圖2是反比例函數y=(n+7)/x圖像中的一支,根據圖像對下述問題進行解答:(1)圖像另一支所處象限是哪個象限?常數n取值范圍是什么?(2)在這個函數圖像的某一支上任取點A(a,b)與B(a,b),若a 這一問題的重點在于對反比例函數增減性加以考查,也即“y在x增大時增大或減小”.由于反比例函數自變量不可是0,故而其增減性并非在整個定義區域范圍中得以表現,而是僅僅在每個象限中表現出增減性,這同樣是中考重點考查內容. 我們選取2010年臺州的一道考題進行分析: 例題2:反比例函數y=6/x圖像上有三個點三者間的關系是() 得知要研究的點并非處于同一象限內,因此不可根據“y隨x增大而減小”這一規律進行判斷,需通過畫圖將這一問題解決,因此答案應選B. 3.k幾何意義分析 練習題三:下列哪個等式內y為x反比例函數? y=4x;y/x=3;y=6x+1;xy=123 在分析時,我們需重點分析xy=123這一式子,這就需要我們對反比例函數圖像知識進行學習時,主要考慮一個問題,那就是反比例函數中的比例系數k與矩形面積間的某一種聯系.K幾何意義為中考最常見的考點之一. 結語 通過分析我們可以看出,在平常學習中,學生應培養鉆研課本習題的良好習慣,對課本習題外延、內涵認真體會,掌握反比例函數的基本題型與解題規律,應用發散性思維,這對于學生學習有重大幫助.

