關注四性，與“歸類”尋實效
——提高學生數學思維能力的策略研究

（蕭山區北干初級中學，浙江 杭州 311203）

新課改有效地改變了傳統教學束縛學生思維發展的舊模式，致力于打造關注學生學習的高效新課堂,為了讓學生學得高效，教師需提高自身的專業素質,探索有效的教學方法——“歸類“教學，培養學生的數學思維能力。針對目前學生的現狀，筆者從課堂教學的一道改編題來具體分析：

【習題呈現】：

拋物線與y軸交于點A，頂點為B，對稱軸BC與x

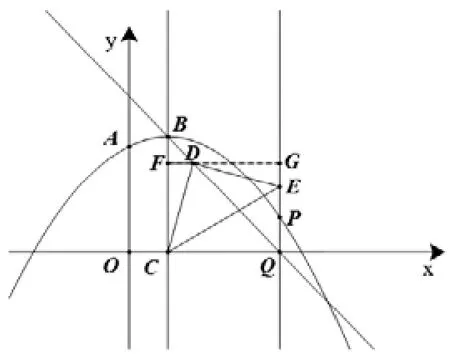
如左圖所示，過點D作x軸的平行線交拋物線對稱軸于點F,交直線PQ于點G，易證△FCD∽△GDE若DCE=30°，則所以1

△GDE與△FCD的相似比為故因為△BFD∽△BC Q，所以化簡得所以點P的橫坐標為將其代入到拋物線的解析式中可得縱坐標為若∠DEC=30°，解法與上述方法一致。再根據圖形的對稱性可得到對稱軸左邊的還有符合條件的兩個P點。

【分析】為什么只有個別學生會解這道題？而且學生的方法并不是解這類題目最簡便、最有效的。筆者分析主要有三個原因：一、學生對知識點不熟悉，不能對相關知識點產生聯想。二、缺乏知識綜合運用能力和推理演繹能力。三、缺乏數學思維能力，平時不注重總結歸納。針對上述學生存在的問題，作為老師應該有意識地對知識點、運用數學方法加以引導。如：1、讓學生回憶圓內接四邊形的對角的數量關系；2、觀察本題中四邊形DCQE相對兩個內角的數量關系；3、從而得出D、C、Q、E四點共圓。所以，這道題又有新解法：

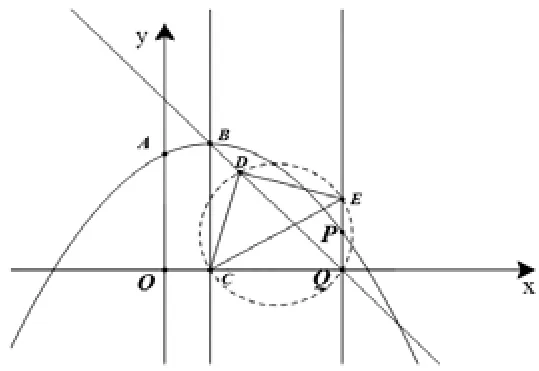
如右圖所示，因為四邊形CQED的內角和為360°，已知∠CDE=∠CQE=90°，所以∠CQE+∠CDE=180°.由CE弦所對兩側的圓周角之和等于 180°，可得 C、D、E、Q 四點共圓.根據同弧所對的圓周角相等，所以∠CQD=∠CED.因為△CDE是含有30°角的直角三角形，且∠CDE=90°，所以∠CED=30°或∠DCE=30°.①當∠CED=30°時，則∠CQD=30°，在直角△BCQ中，由已知可得BC=5，所以.故P點橫坐標為因為P點在拋物線上，其坐標滿足拋物線解析式，把代入解析式可得縱坐標為所以 P點坐標為②當∠DCE=30°時，則∠CQD=∠CED=60°，解法與上同，此時P.由圖形的對稱性，當點P在對稱軸左側時。綜上所述，滿足條件的P點坐標為（

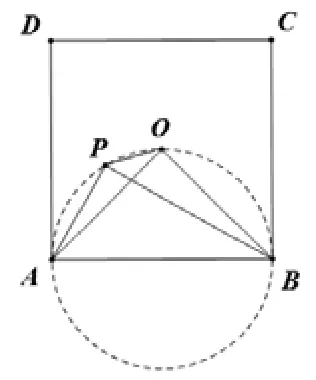
講解完后，學生恍然大悟，都覺得利用輔助圓解題很方便。事實上有些題目看似與圓無關，但用共圓的方法解決能夠避開繁瑣計算，取得最簡便、最有效的方法。因此，必須讓學生掌握這類題目的解法。可是什么時候要用到共圓呢？最有效的方法就是運用“歸類”教學法，舉一反三，以提高學生的數學思維能力，讓學生觸類旁通做到解一題會一類，真正地提高課堂效率，減輕學生負擔。十多年的教學經驗告訴筆者，歸類教學對于提升數學學習效率效果顯著，但因為時間和精力的原因，很多時候還是就題論題，所以我希望通過“歸類共圓”的數學方法展開，談談我對歸類教學的看法。設 GE=a，DG=b，則軸交于點C.點P在拋物線上，直線PQ∥BC交x軸于點Q.若一塊含30°角的直角三角板一個頂點與點C重合，直角頂點D在直線BQ上，另一個頂點E在PQ上，則點P的坐標為___。

在給予學生充分的思考后，全班只有個別學生答對了這道題，而且方法比較復雜：通過設兩個未知數、用三角形相似、整體代入等，計算過程還帶有一定的技巧性。學生思考如下：

一、歸類教學，關注選題的針對性,提高學生逆向思維的能力

設計選題前必須充分考慮預選習題能否加深學生對概念的理解和掌握，或是對錯誤認識的糾正，還是對基本解題技能的進一步熟練等。這就要求教師在選題時要有針對性、目的性。要非常了解學生對知識點的掌握程度，哪些地方掌握得好，哪些地方還存在問題。比如圓的內容，所選的題目最好看似與圓無關，而是讓學生提煉出共圓的方法。也就是說，看似無圓，但事實上隱含著圓，而這個隱身圓就需要學生們去發現。舉例來說：

1.解決有關直角問題

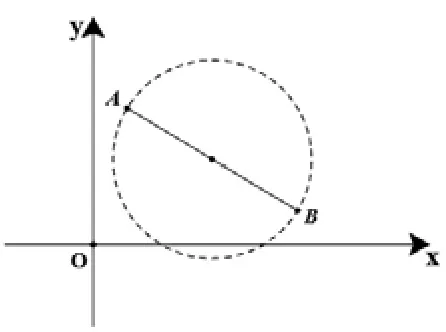
例1：點A、B是平面直角坐標系內的兩個點，且 A（2,4），B（6,2），P 是 x 軸上一點，且△ABP為直角三角形，則滿足條件的點P共有幾個（ ）

（A）1 （B）2 （C）3（D）4

【解析】：△ABP為直角三角形，根據直角頂點分類討論.易知滿足∠PAB=90°的點P有1個；滿足∠PBA=90°的點P有1個；根據直徑所對的圓周角是90°，滿足∠APB=90°的點P在以AB為直徑的圓上.因此，只須判斷圓與x軸的位置關系.由已知A（2,4）、B(6,2)易得圓的半徑圓心到x軸的距離d=3.由d＜r可知圓與x軸相交.所以滿足∠APB=90°的點P有2個.綜上所述，滿足條件的P點共有4個。

【說明】：由上題的啟發，學生容易聯想到圓，而且圓中很重要的結論“直徑所對的圓周角是90°”，從而點P在以AB為直徑的圓上。因此很自然得轉化為判斷直線與圓的位置關系。

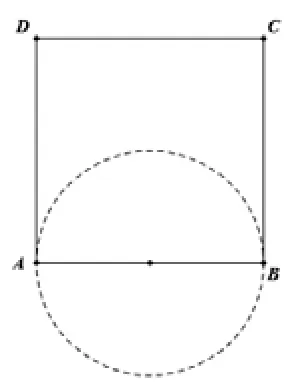
2.解決有關銳角問題

例2：如圖，向正方形ABCD內投一點M，如果正方形內每一點投中的可能性均相同，則使∠AMB為銳角的概率是多少。

【解析】：因為∠AMB為銳角，即∠AMB＜90°，易知使∠AMB=90°的點M在以AB為直徑的圓上.因為小于圓周角的點在圓外，所以所有滿足條件的點M構成的圖形面積為正方形的面積減去半圓的面積。假設正方形邊長為1，則正方形面積為1，半圓面積為

【說明】：由“直徑所對圓周角等于90°”，結合圓外角和圓周角的大小關系，學生還是可以通過輔助圓來解決問題。

3.解決有關鈍角問題

例3：如圖，正方形ABCD的中心為O，P為正方形內一點，若∠OPB=45°,求∠APO的度數。

【解析】：因為O是正方形ABCD的中心，連結OB后，∠AOB＝90°，且∠OAB＝45°與已知∠OPB＝45°相等，可以利用共圓的方法，構造以AB為直徑的圓，易得∠APB＝90°，所以∠APO＝90°+45°＝135°。

【說明】：由“90度的圓周角所對的弦是直徑”和“直徑所對圓周角等于90°”可以很容易的解出此題。

這些例題可以讓學生歸納總結出異側共圓的情形：

除上面這個常見的“共圓”類型外，還有另外一種類型，筆者稱它為同側共圓：

二、歸類教學，關注選題的層次性，提高學生邏輯思維能力

習題的選擇難度要適中，要有梯度。若一開始就太難，容易使學生產生畏懼情緒，做而生煩；若都很容易，太過于淺，又會讓學生產生松懈怠慢心理，也不利于個性思維品質的培養。因此，設計的問題一定要由淺入深、層層遞進。比如：剛開始筆者先出示這樣兩個問題：

1.題設中有公共端點的等線段

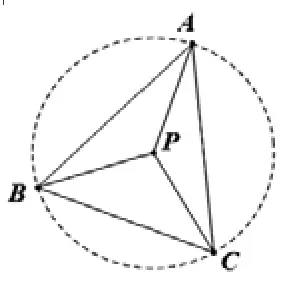
例 4：如圖，在△ABC內有一點 P且PA=PB=PC，若∠PBC=50°∠PBA=30°，則∠APC的大小是（ ）

（A）140°（B）160°（C）80° (D)120°

【解析】：因為PA=PB=PC，所以點A、B、C在以P為圓心、PA長為半徑的圓上.∠ABC=50°+30°=80°，利用同弧所對的圓心角等于圓周角的兩倍關系，∠APC=2∠ABC=160°。

【說明】：已知條件與圓的聯系很明顯，“到一個定點的距離等于定長的點在以這個定點為圓心、定長為半徑的圓上”幾乎所有的學生都容易想到，這也是圓的定義。

2.一條線段同側的兩個角成倍半關系

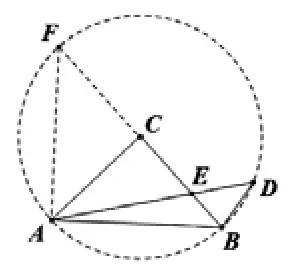
例 5：如圖，若 CA=CB，∠ACB=2∠ADB.BC 與AD 交于點 E，且 CB=10，CE=6，則 AE·DE=()

(A)32 (B)48 (C)64 (D)68

【解析】：∠ACB和∠ADB在線段AB同側，且∠ACB=2∠ADB，CA=CB，根據同弧所對圓心角等于圓周角的兩倍可知點A、B、D在以點C為圓心，CA長為半徑的圓上.延長BC交圓于點 F，連結 AF，那么有∠AFB=∠ADB、∠FAD=∠DBF，故△FAE∽△DBE，所以。由已知 CB=10，CE=6易得 BE=4，EF=16，故 AE·DE=BE·EF=4×16=64。

【說明】：由上一例題得到啟發，學生容易聯想到“同弧所對的圓心角等于圓周角的兩倍”。因此∠ACB為圓心角，∠ADB為圓周角，故可以構造以C圓心，CA長為半徑的圓。

3.一條線段同側的張角不變

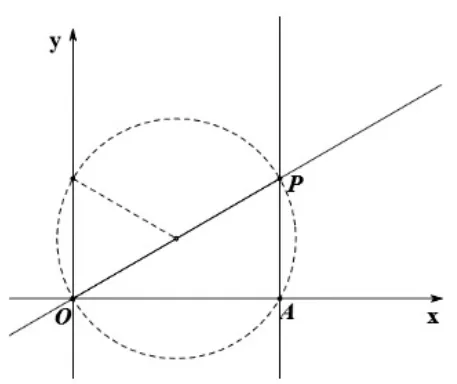
例6：如圖，平面直角坐標系中，直線與直線x=3,于點P，點A是直線x=3與x軸的交點.將直線OP繞著點O、直線AP繞著點A以相同的速度逆時針方向旋轉.旋轉過程中，兩條直線交點始終為P，當直線OP與y軸正半軸重合時，兩條直線同時停止轉動.整個旋轉過程中，點P所經過的路線長為______。

【解析】：由旋轉的性質可得∠OPA始終為60°，過點O、A、P三點作圓，因為∠OAP=90°,根據“90°的圓周角所對的弦是直徑”可得OP為該圓的直徑.當直線OP與y軸正半軸重合時，旋轉過的角度為60°，故點P所走過的弧長所對的圓心角為120°，根據弧長公式可得。

【說明】：本題中∠OPA始終為60°角這個結論很多學生并不能得出，需要作出旋轉后的某個點P，與旋轉前的圖形比較得到。因此這是一個難點，也就要求學生要學會綜合運用，要有較強的分析問題的能力。但可以肯定的是，這樣的問題如果學生能自己解決，那一定能夠提高他的自信心和學數學的興趣。

三、歸類教學，關注題目的可變性,培養學生探究猜想的思維能力

題目的變式、引申可以有以下幾類：1、題目背景、結論不變，變換部分條件；2、題目背景、條件不變，變換結論；3、改變題目背景以及結論，但知識點或方法不變。應用到“歸類”教學，我們可以嘗試解決問題：

1.求兩個共斜邊直角三角形在公共邊異側時的重心距離

例7：我們知道，三角形的三條中線一定會交于一點，這個點就叫做三角形的重心。重心有很多美妙的性質，如有關線段比、面積比就有一些“漂亮”的結論，利用這些性質可以解決三角形中的若干問題。請解答下列問題：將兩塊三角尺按如圖方式拼好，其中∠B=∠D=90°,∠ACD=30°,∠ACB=45°,AC=12,點E,F分別是和的重心，求EF的長。

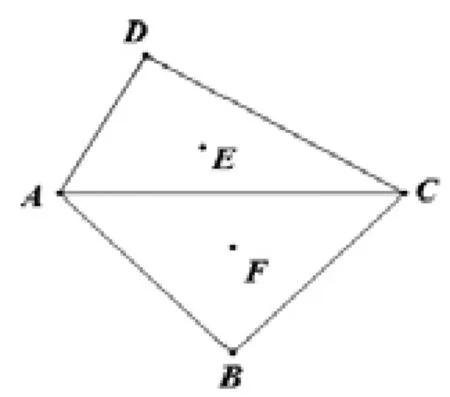
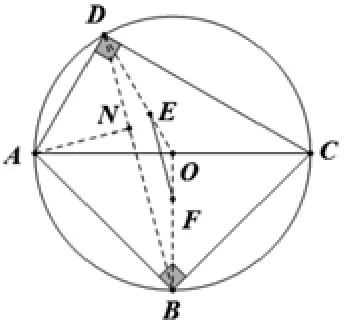
【解析】：因為∠B=∠D=90°,所以A,B,C,D四點在AC為直徑的圓上，如右圖所示，記圓心為點O，連接OD,OB,DB,EF,由重心的性質可知，，所以即問題轉化為求DB的長度。作ANDB，有同弧所對的圓周角相等可知，在RtΔADN中由勾股可得，由已知易得∠NAB=60°，在Rt ΔABN中由30度角三邊關系可得,所以，從而。

以例7為原型，筆者對題目做適當變形，使例題八符合背景不變，條件改變，求結論。重置條件后，可以讓學生動動腦子，稍稍轉下彎，看學生有沒有真正掌握。這樣學生才不會松懈怠慢，也能時時體驗成功的快樂。變式如下：

2.求兩個共斜邊直角三角形在公共邊同側時的重心距離

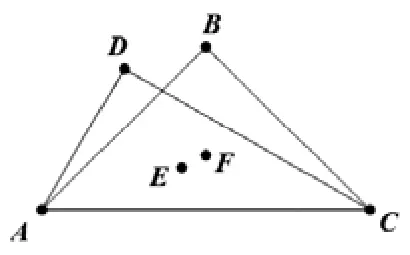
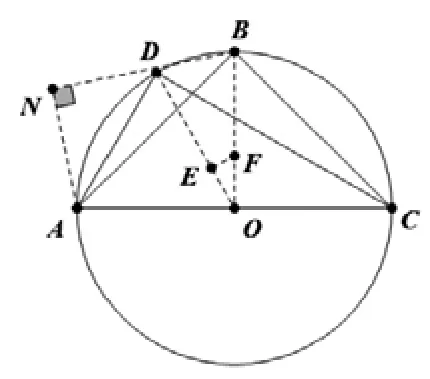
例8：將兩塊三角尺按如圖方式拼好，其中 ∠B=∠D=90° ,∠ACD=30° ，∠ACB=45°，AC=12,點 E,F 分別是 ΔACD和ΔABC的重心，求EF的長。

解析：因為∠B=∠D=90°,所以A,B,C,D四點在AC為直徑的圓上，如圖所示，記圓心為點O，連接OD,OB,DB,EF,由重心的性質可知，所以，即問題轉化為求DB的長度。作AN ⊥DB，因 為 ∠ACB+∠ADB=180° ,∠ADN+∠ADB=180°,所以∠ADN=∠ACB=45°,有同弧所對的圓周角相等可∠NBD=∠ACD=30°,又因為，在Rt ΔADN 中由勾股可得,在Rt ΔABN中由勾股可得,所以，從而。

例8是在例七基礎上的變式，他們既有聯系，又有區別，形別而神同，主要是為了讓學生體會輔助圓解題的便捷，讓學生在以后的解題中能想到這種方法——添加輔助圓。

四、歸類教學，關注題型的發散性，培養綜合分析能力

上述例題圖形簡單，涉及的條件、結論也比較單一，學生比較容易掌握。當孩子自己歸納出輔助圓的方法后，就可以應用在比較復雜的題目中。所以接下來的練習會選擇的圖形比較復雜多樣，問題也都各不相同，而且也基本涵蓋了用輔助圓解決的題目特點。

1.解決有關等腰三角形問題

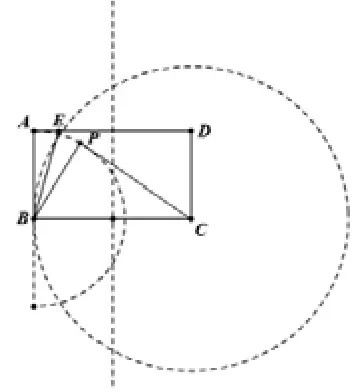
例9：如圖，矩形ABCD中，，點E是折線段A—D—C上的一個動點（點E與點A不重合），點P是點A關于BE的對稱點.在點E運動的過程中，使PCB為等腰三角形的點E的位置共有（ ）。

（A）5個（B）4個（C）3個（D）2個

【解析】：一個P點對應著一個E點，一個E點對應著一個P點，所以只須找出有幾個符合條件的點P.根據折疊的性質可得BP=BA，所以點P一定在以B為圓心、BA長為半徑的⊙B上.又因為點E折線段A—D—C上，故點P在如圖所示的半圓上.因為BP=2、要使PCB為等腰三角形只可能PB=PC、CB=CP兩種情況.PB=PC時，點P在線段BC的中垂線上，該線與⊙B有2個交點，所以存在2個P點使PB=PC；當CB=CP時，點P一定在以C為圓心、CB長為半徑的⊙C上，⊙C與⊙B有2個交點，故存在2個P點使CB=CP.綜上所述，共有4個滿足題意的點P，所以點E的位置有4個。

【說明】：在找等腰三角形時往往需要對頂點進行分類，當已知的兩點構成的線段為腰時都可以通過圓的方法找第三個點。

2.解決有關折疊問題

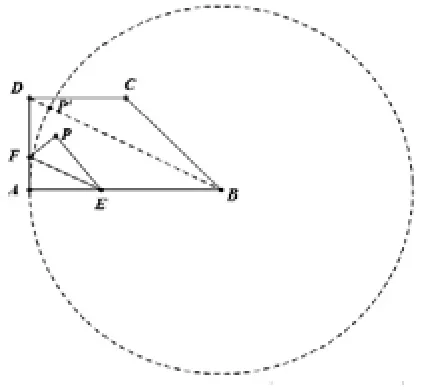
例10：如圖，直角梯形紙片ABCD，AD⊥AB，AD=CD=2，AB=4，點 E、F 分別在線段AB、AD上，將△AEF沿EF翻折，點A的落點記為P. 當P落在直角梯形ABCD內部時，PD的最小值等于____。

【解析】：根據折疊的性質可知EP=EA，所以點P一定在以E為圓心、EA長為半徑的圓上.因為點P要在直角梯形ABCD內部，故點P落在梯形內的圓弧上.當點E越靠近B點時，圓的半徑越大，所以圓弧上的點離點D越近，當E點在B點時半徑最大，圓弧離點D最近.而在圓弧上的所有點中又有一個點離點D最近，易知該點就是直線BD與圓的交點,如圖所示即為P’.因為AD=2、AB=4，所以由勾股定理得.故PD的最小值為。

【說明】：折疊時對應邊的長度始終相等，且到折痕的某個端點的距離相等。故可以構造折疊前后的兩個對應點共圓。

3.解決有關旋轉問題

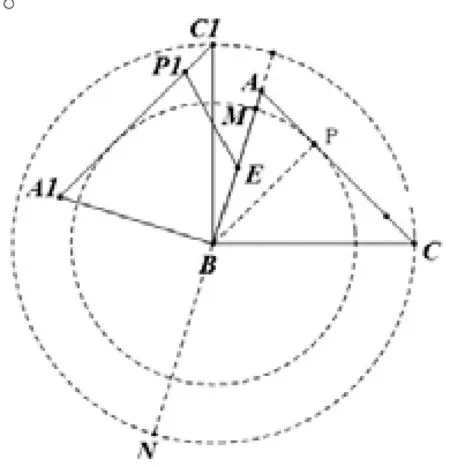
例11：如圖，在銳角ABC中，AB=8，BC=10，∠ACB=45°，將ABC繞點B按逆時針方向旋轉，得到.點E為線段AB中點，點P是線段AC上的動點，在ABC繞點B按逆時針方向旋轉過程中，點P的對應點是點P1，求線段長度EP1的最大值與最小值。

【解析】：根據旋轉的性質，點P1在以B為圓心、BP長為半徑的圓上.圓上與點E最近、最遠的兩個點便是直線BE與圓的兩個交點.易知當時.如圖所示，在以B為圓心、BP長為半徑的圓上，與點E最近的是M點，所以EP1的最小值即為EM的長.因為已知AB=8,BC=10，∠ACB=45°，易知；當EP1的長度最大時，半徑BP要最大，即點P在以C點為圓心，以BC為半徑的圓上，如圖所示，與點E最遠的是N點，易知EN=EB+BN=4+10=14，綜上所述，EP1長度的最大值是14，最小值是。

【說明】：任何圖形的旋轉最終都是點關于點的旋轉。因為一個點繞著另一個點旋轉的過程中始終保持著距離不變，所以旋轉得到的所有點共圓，該圓的圓心就是旋轉中心、半徑就是這兩個點之間的距離。所以許多旋轉的問題可以通過添加輔助圓來解決。

4.解決有關特殊角問題

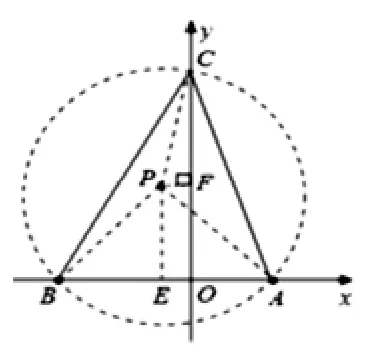
例12：在平面直角坐標系中，已知點A（4，0）、B（-6，0），點 C 是 y 軸上的一個動點，當∠BCA=45°時，求點C的坐標。

【解析】：如圖所示，取AB中點E，作EP⊥BA，且，易知△PBA為等腰直角三角形，。以點P為圓心，PA長為半徑作⊙P，與y軸的正半軸交于點C，因為∠BCA為⊙P的圓周角，所以∠BCA=，則點C即為所求。過點 P作 PF⊥y軸于點 F，則OF=PE=5，PF=1，在，由勾股定理得 CF=7，所以OC=OF+CF=5+7=12。所以點C坐標為（0，12）。根據圓的對稱性質，可得y軸負半軸上的點C坐標為（0，-12）。綜上所述，點 C坐標為（0，12）或（0，-12）。

【說明】：本題的突破口應該是∠BCA=45°這個條件，45°是一個特殊角，從這個角度入手我們可以構造直角三角形，而直角三角形又可以到圓中去找，這樣就想到了構造輔助圓的方法。在數軸上一個數據就能確定一個點的位置，在平面直角坐標系中要兩個數據才能確定一個點的位置，在本題中圓和弦的交點恰好就是所求的點C,轉化到運用幾何的知識解決，自然而然，事半功倍。

我們都知道數學能力有兩個方面，一是運算能力，一是思維能力。運算能力是一種基礎能力，強調記憶、熟練度（復雜運算需要一些技巧），思維能力才是一種高級能力，強調借助抽象的數字符號、概念進行思考與推理。由本文例題可以看出，原題圖中都沒有圓，當解題時添上輔助圓后，問題就迎刃而解，讓學生們體會輔助圓的妙用，做到題中無圓，心中有圓。作為一線數學教師，在平時的課堂中應用“歸類”教學法引導學生對知識的內在聯系有更深一步的理解，側重思維訓練，讓學生真正做到解一題會一類，掌握數學學習方法。既培養學生的數學思維能力,又提高課堂效率，于“歸類教學”中尋實效，是走向輕負高效的一條可行之路，一條快捷之路，也是一條必由之路。

[1]孔慧英，梅智超編著，現代數學思想概論。北京：中國科學技術出版社，1993

[2]錢學森主編，關于思維科學。上海：上海人發出版社，1986

[3]郭思樂、喻偉著，數學思維教育論。上海：上海教育出版社，1997

[4]朱智賢、林崇德，思維發展心理。北京師范大學出版社，1990

[5]席振偉著，數學的思維方式。南京：江蘇教育出版社，1995