毛紗捻縮率的預測模型

陶建勤， 余曉華， 張宏偉， 劉 娜

(1. 常州紡織服裝職業技術學院， 江蘇 常州 213164； 2. 常州市新型紡織材料重點實驗室， 江蘇 常州 213164；3. 常州三毛紡織集團有限公司， 江蘇 常州 213017)

毛紗捻縮率的預測模型

陶建勤1，2， 余曉華1，2， 張宏偉1，2， 劉 娜3

(1. 常州紡織服裝職業技術學院， 江蘇 常州 213164； 2. 常州市新型紡織材料重點實驗室， 江蘇 常州 213164；3. 常州三毛紡織集團有限公司， 江蘇 常州 213017)

為提高毛紗質量與毛紡工藝設計效率，通過理論推導與實驗驗證，建立毛紗捻縮率的預測模型。在截取毛紗橫截面幾何模型的基礎上，逐步導出捻縮率與相關因素之間的數學關系。結果表明，根據所紡毛紗的線密度、捻度要求以及所用原料的平均直徑與平均體積密度，利用毛紗捻縮率預測模型可以快速地獲得捻縮率預測值；將捻縮率預測值用于計算細紗機前羅拉出條定量、選配捻度變換齒輪組時，毛紗的線密度偏差率與捻度偏差率可被有效地控制在FZ/T 22001—2010《精梳機織毛紗》中優等品毛紗所規定的范圍內。

毛紗； 捻縮率； 預測模型； 工藝設計效率

捻縮率直接影響成紗的線密度與捻度[1]，是紡紗工藝設計時必須考慮的重要因素[2-3]。在現有生產中，捻縮率通過實測細紗機前羅拉輸出的紗條長度及其管紗上對應的細紗長度，利用捻縮率定義式計算得出，即必須在試紡過程中測得。而在紡紗工藝設計階段所用的捻縮率一直以來是憑經驗取值，存在較大的不確定性，影響成紗的規格精度[4-5]，尤其是開發新品時往往因取值依據不足而降低工藝設計效率。據資料顯示，國內已有關于毛紗捻縮率預測方面的研究，但所示方法復雜、繁瑣，且仍有需要憑經驗取值的環節[6]，至今在生產實踐中未推廣應用。

本文在理論分析、推導與實驗驗證的基礎上，研究純羊毛紗和羊毛/化纖混紡紗的捻縮率預測模型，使毛紡工藝設計者不需通過試紡過程就能有效預測所紡毛紗在細紗生產時的捻縮率，從而提高毛紗規格精度、提高毛紡工藝設計效率。

1 模型建立

1.1 毛紗橫截面幾何模型的截取

在測試成紗線密度與捻度時，試樣均處于凈長狀態，因此，捻縮率在理論上應該是紗條在加捻前后的凈長差值占加捻前凈長值的百分率。紗條凈長是指其中纖維縱向接近伸直平行、橫向接近密排狀態下的紗條長度。

毛纖維的橫截面近似圓形，且加捻過程會促使其紗條橫向結構趨于緊密、橫截面形狀趨于圓整，因此，以毛纖維為原料的紗條在加捻前后的橫截面幾何模型可從順序堆積的纖維集合體橫截面中截取，如圖1所示。以紗條軸線為中心，由內而外分布的纖維層數隨著紗條直徑的增大而增多，相鄰2層之間的纖維數量差異為6根，每個纖維層中的纖維分布呈現以F纖維為中心的正六邊形。圖中：F表示沿紗條軸線排列的纖維；a為最外層纖維所在的正六邊形邊長，μm；df為毛纖維的平均直徑，μm；dx為使內外纖維根數相等的分割圓直徑，μm；ds為紗條的當量直徑，μm。

1.2 毛紗當量直徑計算式的推導

若紗條橫截面內共有M層纖維，如圖1所示，則最外層纖維所在的正六邊形包含的平均纖維根數n可以通過式(1)計算，考慮到毛紗橫截面內平均纖維根數在生產實際中是一選取值，因此，利用堆壘級數部分和的一般公式[7]，將式(1)轉換成式(2)，在此基礎上進一步轉換成式(3)；根據圖1所示的幾何關系可知，該正六邊形的邊長等于其外接圓的半徑，與毛纖維平均直徑的關系如式(4)所示，則該正六邊形的面積計算式如式(5)所示[8]。

如圖1所示，考慮到加捻后毛紗橫截面近似圓形，為此對其最外層纖維所在的正六邊形進行圓形修正，使其面積等于修正圓的面積，其等量的面積關系如式(6)所示。

(6)

將式(6)轉化成式(7)，并將式(3)代入式(7)得到式(8)，用以計算紗條當量直徑。

1.3 紗體分割圓直徑計算式的推導

加捻時，紗體內纖維處于動態平衡過程，纖維之間沿縱向產生靜摩擦而使所有纖維趨于張緊，各層纖維的張緊程度由內而外逐層遞增；因纖維張緊及其內外層張緊程度的差異，使外層纖維對內層纖維產生擠壓作用，迫使部分纖維發生內外轉移；內外不同層次的纖維沿紗條軸線呈現不同程度的螺旋形分布，使各層纖維對紗體長度的縮短產生不同程度的作用。紗體由內而外的各層母線在加捻前長度相等且等于紗條原長；理論上,加捻過程中各層母線逐漸演變成螺旋線且由內而外螺旋程度逐層遞增，使紗體由內而外母線長度逐層遞減。為兼顧內外層纖維在加捻過程中動態表征的層次遞變效應與層次互動效應，在圖1所示的修正圓中虛擬一個分割圓，使分割圓內外的纖維根數相等，由此得到式(9)。

(9)

式中：SN為分割圓的圓內面積，μm2；SW為分割圓的圓外面積，μm2；Sf為毛纖維橫截面的平均面積，μm2。

將式(9)中的各項分別轉換成面積計算式，如式(10)所示。

(10)

式中：dx為分割圓的直徑，μm；r為半徑，μm。

在此基礎上將式(10)轉換成式(11)，利用式(11)計算dx值得到要求的分割圓，以分割圓所在紗體層在加捻前后的母線長度計算毛紗捻縮率。

(11)

1.4 毛紗捻縮率預測模型的構建

假設T為毛紗名義捻度，捻/m；T′為細紗生產過程中對1 m長紗條的應加捻回數，捻/m。則T與T′之間的關系如式(12)[9]所示。

T′=T×(1-c)

(12)

式中c為毛紗捻縮率，%。

圖2示出加捻過程中分割圓所在紗體層的母線軌跡展開示意圖。圖中，AB為紗條加捻前分割圓所在紗體層的任一母線，設其長度為1 m；如果加捻時使紗條的B端所在截面回轉，當加上T′個捻回后，B點將在其所在截面處轉過T′圈，其有效位移量為π×dx×T′，同時，母線AB的運動軌跡呈動態螺旋線，加捻結束時螺旋線的形態得到穩定；將加捻后由B點旋轉而產生的有效位移、母線AB演變成的螺旋形軌跡以及原AB母線所在位置線AB′三線共同構成的一個隱性面鋪展開來，得到圖2中的直角三角形AB′E，顯然，母線AB演變成的螺旋線進一步演變成展開圖中的直角三角形AB′E的斜邊AE，且AE=AB=1 m，則其直角邊AB′的長度即為1 m長紗條獲得T′個捻回后的毛紗長度。

根據捻縮率定義，結合式(11)，得到對應的捻縮率計算式(13)，再將式(8)與式(12)分別代入式(13)得到式(14)，經轉換進一步得到捻縮率c的求解式，如式(15)所示。

1.4.1 純羊毛紗捻縮率預測模型

若紡制純羊毛紗，則毛紗橫截面平均羊毛根數與羊毛平均直徑之間的關系如式(16)[10]所示。

(16)

式中：dw為羊毛的平均直徑，μm；Nt為毛紗的實紡線密度，tex。

將式(16)經轉換得到式(17)，再將dw與式(17)代入式(15)得到式(18)。工藝設計時，根據所紡純羊毛紗的實紡線密度、名義捻度以及所選羊毛的平均直徑，利用式(18)預測其細紗生產過程的捻縮率。

(17)

(18)

1.4.2 羊毛/化纖混紡紗捻縮率預測模型

若紡制羊毛/化纖混紡紗，并假設q為所用成分纖維的種類數；dh、di分別為混合原料與某成分纖維的平均直徑,μm；γh、γi分別為混合原料與某成分纖維的的平均體積密度，g/cm3；pi為某成分纖維的公定質量百分比，%。則有關系式(19)～(21)[10]，將式(19)與(20)同時代入式(21)得到式(22)，再將式(19)與式(22)同時代入式(15)得到式(23)。工藝設計時，根據所紡混紡毛紗的實紡線密度、名義捻度、各成分纖維的公定質量百分比以及相應成分纖維的平均直徑與平均體積密度，利用式(23)預測其細紗生產過程的捻縮率。

(19)

(20)

(21)

(22)

(23)

2 實驗驗證

以4種精梳機織用毛紗為例，相關設計要求及所用原料的相關信息如表1所示。

2.1 實驗部分

2.1.1 毛紗捻縮率的預測

編號為1和2的純羊毛紗捻縮率預測值利用式(18)計算；編號為3和4的混紡毛紗捻縮率預測值利用式(23)計算。利用式(23)時，各種成分纖維所需的公定質量百分比利用式(24)計算。

(24)

式中：P0i為某種成分纖維在毛紗中要求的混紡比，%；WKi為該種成分纖維的公定回潮率，%。

2.1.2 細紗工序相關工藝的設計

細紗生產采用B583C型細紗機。

工藝設計時，以捻縮率預測值為依據，細紗機前羅拉出條定量的計算如式(25)所示。

表1 毛紗設計要求與所用原料相關信息Tab.1 Design requirement of wool yarn and data of its raw materials

(25)

式中G為細紗機前羅拉出條定量，g/m。

同時，依據毛紗名義捻度，利用式(12)確定細紗生產過程中對1 m長紗條的應加捻回數計算值，再進一步從相應細紗機的《捻度變換表》中查得與該計算值最接近的捻度值作為捻度選擇值，同時確定各捻度變換齒輪的齒數。

2.1.3 毛紗捻縮率的測試

采用傳統的方法，在試紡過程中先分別測量細紗機前羅拉輸出的紗條長度與管紗上退繞的細紗長度，再利用捻縮率定義式計算捻縮率。捻縮率的誤差率△c利用式(26)計算。

(26)

式中c′為毛紗捻縮率實測值，%。

在測試捻縮率基礎上，通過計算誤差率分析毛紗捻縮率預測模型的顯性效果。

2.1.4 毛紗規格的測試

依據FZ/T 20017—2010《毛紗試驗方法》對試紡毛紗線密度進行測試；依據GB/T 2543.2—2001《紗線捻度的測定 第2部分：退捻加捻法》對試紡毛紗捻度進行測試。線密度偏差率與捻度偏差率的等級評判依據FZ/T 22001—2010《精梳機織毛紗》進行。通過測試線密度及其偏差率、捻度及其偏差率，分析毛紗捻縮率預測模型的潛在工藝效果。

2.2 結果與分析

表2示出毛紗捻縮率預測值及其工藝效果。可知，捻縮率預測值與其實測值之間存在較小誤差。客觀上，捻縮率測試時，細紗機前羅拉輸出的紗條長度與管紗退繞的細紗長度在測量過程中分別存在系統誤差與偶然誤差，故針對毛紗的具體品種，細紗生產時的捻縮率實測值是個不確定值；而捻縮率預測值則取決于所紡毛紗的實紡線密度、名義捻度以及所用纖維的平均直徑與平均體積密度，因此是個確定值。

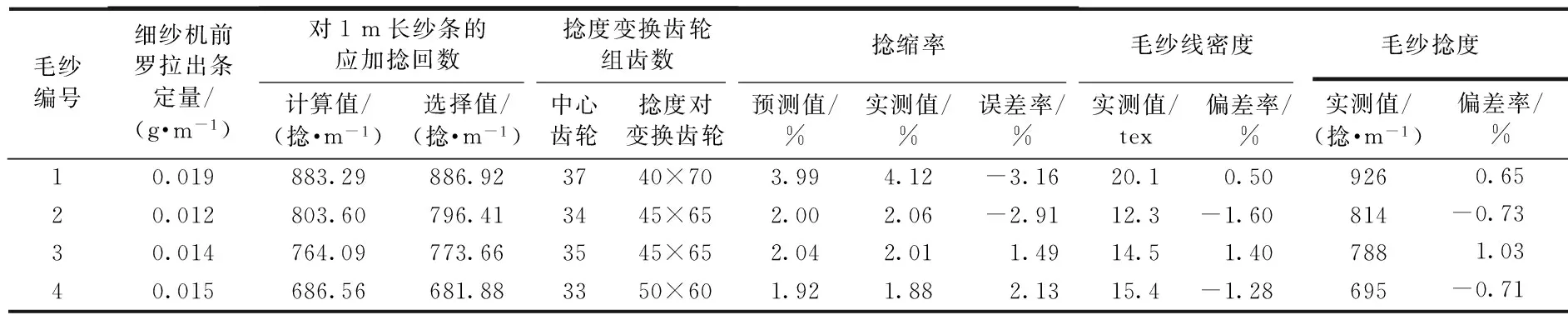
表2 毛紗捻縮率預測值及其工藝效果Tab.2 Wool yarn twist shrinkage value and its effect

另據FZ/T 22001—2010《精梳機織毛紗》可知，優等品毛紗所規定的線密度偏差率與捻度偏差率范圍分別為±2.0%與±6.0%。表2顯示，試紡紗的線密度偏差率與捻度偏差率數據均在優等品毛紗所要求的范圍內，而且具體數據較為理想，因此，利用本文建立的毛紗捻縮率預測模型所得到的捻縮率預測值應用于細紗工藝設計時，相關工藝效果超預期。

3 結 論

1)毛紡細紗生產時，紗條的捻縮率不僅取決于所紡毛紗的線密度、捻度，還取決于所用原料的平均直徑與平均體積密度。

2)毛紡工藝設計時，根據所紡毛紗的規格要求與相關原料信息，選用本文推導的公式能快速預測純羊毛紗或羊毛/化纖混紡紗在細紗生產時的捻縮率，并為細紗機前羅拉出條定量的計算、捻度變換齒輪組中各齒輪齒數的選配提供準確依據。

[1] 張一心.紡織材料[M].2版. 北京：中國紡織出版社,2010:272. ZHANG Yixin. Textile Material[M]. 2nd ed. Beijing： China Textile & Apparel Press, 2010:272.

[2] 陸亞建.成品支數縮率研究[J].毛紡科技,2000(3):41-43. LU Yajian. Finished product count shrinkage [J]. Wool Textile Journal, 2000(3):41-43.

[3] 戚傲春. 精梳毛紗細度偏差的控制[J]. 上海紡織科技, 2007(5):9-11. QI Aochun. Fineness deviation control of worsted wool yarn[J]. Shanghai Textile Science and Technology, 2007(5):9-11.

[4] 李學彬,邢少麗.精紡毛織物設計與創新探討[J].毛紡科技,2000(增刊):25-26. LI Xuebin, XING Shaoli. Worsted textile design and enovation discussion[J]. Wool Textile Journal, 2000(Supplement):25-26.

[5] 潘偉, 聞艷萍, 周玉潔.毛精粗紡結合走產品創新之路[J].天津紡織科技,2011(5):39-40. PAN Wei, WEN Yanping, ZHOU Yujie. Enovation with woolen and worsted combination [J]. Tianjin Textile Science and Technology, 2011(5):39-40.

[6] 劉仲康.毛紗捻縮的理論分析[J].毛紡科技,1984(2):31-43. LIU Zhongkang. Theoretical analyses on wool yarn twist shrinkage[J]. Wool Textile Journal,1984(2):31-43.

[7] 數學手冊編寫組.數學手冊[M].北京：高等教育出版社, 1979:11. Math Handbook Compile Group. Math Handbook[M]. Beijing：Higher Education Press, 1979:11.

[8] 奈次. 數學公式[M].石勝文,譯. 北京：海洋出版社,1983:86. NAI Ci. Math Formula[M]. SHI Shengwen, Translating. Beijing：Ocean Press, 1983:86.

[9] 陳錫勇,陶建勤.紡織工藝設備實訓[M].北京：化學工業出版社,2014:28. CHEN Xiyong, TAO Jianqin. Practice on Textile Technology and Equipment [M]. Beijing： Chemical Industry Press, 2014:28.

[10] 陶建勤,張宏偉,陳錫勇,等.以品質指數為導向的精梳純毛紗條干質量控制[J].紡織學報,2014,35(11):28-34. TAO Jianqin, ZHANG Hongwei, CHEN Xiyong, et al. Evenness quality control for worsted pure wool yarn based on quality index number [J]. Journal of Textile Research, 2014,35(11):28-34.

Prediction model on twist shrinkage of wool yarn

TAO Jianqin1，2， YU Xiaohua1，2， ZHANG Hongwei1，2， LIU Na3

(1.ChangzhouTextileGarmentInstitute，Changzhou，Jiangsu213164，China；2.KeyLaboratoryofChangzhouNewTextileMaterial，Changzhou，Jiangsu213164，China； 3.TheThirdChangzhouWoolTextileGroupCo.，Ltd.，Changzhou，Jiangsu213017，China)

In order to improve the precision of wool yarn specifications and the design efficiency of wool spinning technology, a wool yarn twist shrinkage prediction model was established by theoretical deduce and experimental reasoning. Based on the geometry model of wool yarn cross-section, mathematical equations among twist shrinkage and relative factors were deduced step by step. The results show that wool yarn twist shrinkage prediction value can be easily obtained by providing some factors such as wool yarn linear density, yarn twist, fiber mean diameter and fiber mean specific density. When the predicted shrinkage value is used in calculation of yarn linear density and in selection and combination of twist gears, the deviation ratios of wool yarn linear density and twist were within the prescriptive scope of "FZ/T 22001—2010 Worsted Woven Wool Yarn".

wool yarn； twist shrinkage； prediction model； technology design efficiency

10.13475/j.fzxb.20150302706

2015-03-16

2016-02-15

陶建勤(1965—)，女，副教授。研究方向為毛紡織原料及其加工新技術。E-mail: taojianqinmf@126.com。

TS 131.9

A