一題一課：讓復(fù)習(xí)課走向簡約與關(guān)聯(lián)
——以一元二次方程章末復(fù)習(xí)課為例

☉江蘇省如東縣實(shí)驗(yàn)中學(xué)　謝桂芬

?

一題一課：讓復(fù)習(xí)課走向簡約與關(guān)聯(lián)
——以一元二次方程章末復(fù)習(xí)課為例

☉江蘇省如東縣實(shí)驗(yàn)中學(xué)謝桂芬

一、寫在前面

張奠宙教授曾對復(fù)習(xí)課研究提出一些指導(dǎo)意見，建議要加強(qiáng)章末復(fù)習(xí)課的研究.從近兩年《中學(xué)數(shù)學(xué)》（初中版）刊載文章來看，確實(shí)出現(xiàn)了不少優(yōu)秀的章末復(fù)習(xí)課例成果，展示出老師們對復(fù)習(xí)課型的最新思考和教學(xué)流程，筆者也受益其中.適逢學(xué)校近期一次教研活動(dòng)，有機(jī)會(huì)執(zhí)教一元二次方程章末復(fù)習(xí)課，筆者也構(gòu)思了一節(jié)“一題一課”，得到觀摩老師的一致好評，本文記錄該課的教學(xué)設(shè)計(jì)與教后反思，與更多的同行分享與研討.

二、一元二次方程章末復(fù)習(xí)課例

（一）開課階段，情境引入

情境問題：用一根長為24m的繩子圍出一個(gè)長方形.

（1）當(dāng)長是寬的2倍時(shí)，長和寬各是多少？

（2）當(dāng)它的面積是32m2時(shí)，長和寬各是多少？

教學(xué)預(yù)設(shè)：（1）設(shè)寬為xm，長為2xm，2x+4x=24，6x= 24，解得x=4，于是2x=8，所以長是8m，寬是4m.

有學(xué)生會(huì)覺得，老師用這個(gè)例子想說明什么呢？這里是復(fù)習(xí)一元二次方程呀，怎么變成一元一次方程了呢？其實(shí)我們只要把問題稍作變式，到了第二問，一元二次方程就出來了！

（2）類似地可設(shè)長為xm，可得方程x（12-x）=32，這是一個(gè)什么方程呢？是一元二次方程嗎？

學(xué)生應(yīng)該能確認(rèn)這種方程的類型：一元二次方程.

但也有少數(shù)學(xué)生可能還沒有看“清楚”，這是因?yàn)檫€沒有把x（12-x）=32變形成一般形式：-x2+12x-32=0，還可進(jìn)一步變形為：x2-12x+32=0.（注意追求二次項(xiàng)系數(shù)為正的，有利于后續(xù)運(yùn)算或求解）這里需要再強(qiáng)調(diào)一下一元二次方程的一般形式：ax2+bx+c=0（a、b、c為常數(shù)，其中a≠0）.

從一般形式中對常數(shù)a、b、c的限制來看，b、c是可以為任意實(shí)數(shù)的，比如上面得到的一元二次方程x2-12x+ 32=0，如果做些刪減，變成：x2=0，x2-12x=0，x2+32=0，它們還是一元二次方程嗎？（注意對照定義來判定）回答是肯定的.

（二）復(fù)習(xí)解法

針對上面得到的三個(gè)“簡化”后的方程：x2=0，x2-12x=0，x2+32=0，安排學(xué)生求解.

教學(xué)預(yù)設(shè)：對于前兩種方程、學(xué)生利用直接開方、因式分解，都可以順利求解，不是本課復(fù)習(xí)重點(diǎn).而x2+32= 0，根據(jù)平方根的意義是不能求解的，也就是說這雖然是一元二次方程，但它卻沒有實(shí)數(shù)解！

（2）繼續(xù)復(fù)習(xí)，配方法解方程：x2-12x+32=0.

教學(xué)預(yù)設(shè)：將其配方成x2-12x+36=4，（x-6）2=4，x-6=±2，所以x-6=2或x-6=-2，即x1=8，x2=4.

（3）復(fù)習(xí)推導(dǎo)一元二次方程的求根公式.

教學(xué)預(yù)設(shè)：引導(dǎo)學(xué)生推導(dǎo)出一般形式的一元二次方程ax2+bx+c=0（a≠0）的求根公式：

教學(xué)預(yù)設(shè)：待學(xué)生推導(dǎo)出來之后，安排學(xué)生利用公式法解方程x2-12x+32=0！

明確提出規(guī)范表達(dá)的要求：

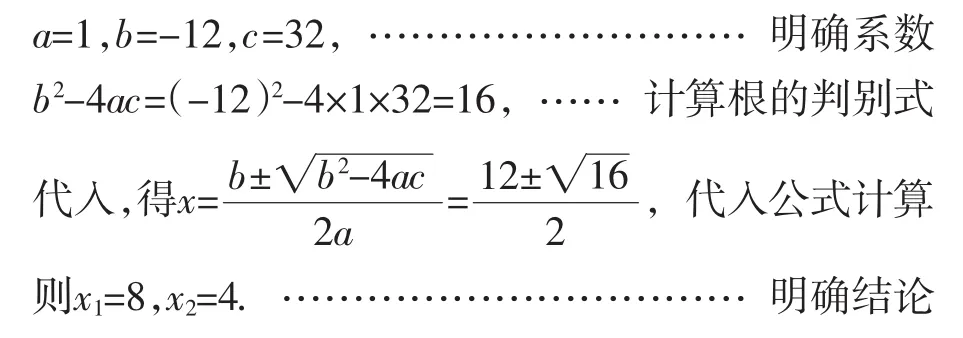
教學(xué)預(yù)設(shè)：需要提醒學(xué)生的是，運(yùn)用公式法解方程，不宜跳步，要規(guī)范表達(dá)上述步驟，因?yàn)殡S意跳步不但會(huì)增加算錯(cuò)的風(fēng)險(xiǎn)，還是對規(guī)范表達(dá)的漠視，可不是一個(gè)好習(xí)慣呀！比如，提供一個(gè)錯(cuò)誤解答讓學(xué)生參與辨析.

錯(cuò)例辨析：解方程：x2-4x+1=0.

分析：這個(gè)學(xué)生喜歡跳步解答，因?yàn)椤疤保统霈F(xiàn)了代入算錯(cuò)的情形.

（三）根的判別式及應(yīng)用

拓展問題：用一根長為24m的繩子圍成的長方形，面積能否等于40m2？

教學(xué)預(yù)設(shè)：根據(jù)前面的經(jīng)驗(yàn)，學(xué)生可以列出方程：x（12-x）=40，并且變形為一般形式：x2-12x+40=0，運(yùn)用配方或求根公式法都會(huì)發(fā)現(xiàn)該方程是無解的，從而發(fā)現(xiàn)面積不可能等于40m2.

繼續(xù)追問：用一根長為24m的繩子圍成的長方形，最大能圍成的面積是多少呢？

教學(xué)預(yù)設(shè)：引導(dǎo)學(xué)生將這個(gè)問題“數(shù)學(xué)化”：關(guān)于x的方程為x（12-x）=S，求S的最大值.

將其“一般化”：x2-12x+S=0.根據(jù)一元二次方程求根公式中根的判別式，Δ=b2-4ac=144-4S≥0時(shí)，方程有實(shí)數(shù)解，即S≤36，即S的最大值為36，也就是用一根長為24 m的繩子圍成的長方形，最大能圍成的面積是36m2.

（四）小結(jié)與檢測

（1）把上面提到的一些知識(shí)或方法用下圖總結(jié)出來，供學(xué)生復(fù)習(xí)與體會(huì)：

（2）由于課堂教學(xué)時(shí)間原因，這一章還有很多值得拓展復(fù)習(xí)的內(nèi)容，比如一元二次方程根與系數(shù)的關(guān)系，一元二次方程的應(yīng)用問題等.

（3）限時(shí)檢測（一共6小題，每小題20分，滿分120分，限時(shí)10分鐘）

已知一元二次方程x2+bx+c=0.解答下列各題：

（1）當(dāng)b=2，c=1時(shí)，直接寫出方程的兩個(gè)實(shí)數(shù)根；

（2）當(dāng)b=4，c=3時(shí)，用配方法解方程；

（3）當(dāng)b=5，c=4時(shí)，用求根公式法解方程；

（4）當(dāng)b=6時(shí)，方程一定有實(shí)數(shù)根，求c的取值范圍；

（6）若點(diǎn)（b，c）在直線y=x-1上，試判斷方程解的情況，并說明理由.

三、教后反思

1.一題一課讓復(fù)習(xí)環(huán)節(jié)走向關(guān)聯(lián)

坦率地講，當(dāng)下不少復(fù)習(xí)課仍然存在著以大量習(xí)題訓(xùn)練講評代替復(fù)習(xí)課的教學(xué)設(shè)計(jì)，導(dǎo)致學(xué)生復(fù)習(xí)期間課上做題、課后做題，機(jī)械重復(fù)，特別是優(yōu)秀學(xué)生“空轉(zhuǎn)”現(xiàn)象嚴(yán)重.所以預(yù)設(shè)“一題一課”可以讓不同復(fù)習(xí)環(huán)節(jié)走向關(guān)聯(lián)，將不同的復(fù)習(xí)內(nèi)容放置在一個(gè)大的情境問題的背景之下，使學(xué)生理解由一個(gè)問題出發(fā)，以點(diǎn)帶面，復(fù)習(xí)整章內(nèi)容，而且使這一章的諸多內(nèi)容獲得了一個(gè)主線，讓學(xué)過的知識(shí)像葡萄一樣串成一條線.

2.一題一課讓復(fù)習(xí)流程平滑轉(zhuǎn)場

我們知道，優(yōu)秀文學(xué)、影視作品都努力經(jīng)營著轉(zhuǎn)場效果，使得前后片斷的轉(zhuǎn)接自然而然.然而，我們現(xiàn)在看到的很多數(shù)學(xué)課堂，多是講解新知后加一個(gè)例題，再來一個(gè)不同方向的例題，一組基本無關(guān)的練習(xí)，這樣的教學(xué)流程讓數(shù)學(xué)變得機(jī)械而無趣.所以我們構(gòu)思一題一課還有一個(gè)好處，就是讓不同的教學(xué)流程之間變得可以平滑轉(zhuǎn)場.比如，本文中在拓展思考時(shí)就是針對開課前的情境，很自然地思考圍成長方形的面積能否達(dá)到40m2，引出根的判別式的復(fù)習(xí)，并進(jìn)一步思考圍成面積的最大值.

3.一題一課需要對話追問和訓(xùn)練

當(dāng)一題一課使得課堂環(huán)節(jié)變得簡約之后，就需要預(yù)設(shè)不同教學(xué)環(huán)節(jié)之中的對話與追問，通過對話拓展學(xué)生的思考，暴露學(xué)生的思維，使得學(xué)生理解得更全面、深刻，讓不同的人有不同的理解深度.同時(shí)也要加強(qiáng)訓(xùn)練，比如引入錯(cuò)題剖析，小結(jié)時(shí)及時(shí)檢測反饋，確保復(fù)習(xí)效果.

四、寫在最后

一題一課的實(shí)踐還很初步，在《中學(xué)數(shù)學(xué)》（初中版）上也散見少數(shù)課例體現(xiàn)了簡約、關(guān)聯(lián)的追求，期待有興趣的同行一起研究、豐富案例.

參考文獻(xiàn)：

1.章建躍.從數(shù)學(xué)整體觀看“同底數(shù)冪的乘法”的教學(xué)［J］.中國數(shù)學(xué)教育，2013（7/8）.

2.嚴(yán)莉.對一份“習(xí)題單”式導(dǎo)學(xué)案的商榷——以“有理數(shù)乘法（第1課時(shí)）”為例［J］.中學(xué)數(shù)學(xué)（下），2014（11）.

3.章建躍.構(gòu)建邏輯連貫的學(xué)習(xí)過程使學(xué)生學(xué)會(huì)思考［J］.數(shù)學(xué)通報(bào)，2013（6）.Z