基于剛度反演的大型振動篩減振彈簧健康識別

彭利平，劉初升，王　宏

(1．河海大學機電工程學院，江蘇常州　213022;2．中國礦業大學機電工程學院，江蘇徐州　221116;3．中煤科工集團 唐山研究院有限公司，河北唐山　063012)

?

基于剛度反演的大型振動篩減振彈簧健康識別

彭利平1，劉初升2，王宏3

(1．河海大學機電工程學院，江蘇常州213022;2．中國礦業大學機電工程學院，江蘇徐州221116;3．中煤科工集團 唐山研究院有限公司，河北唐山063012)

摘要:針對已有的大型振動篩減振彈簧定性健康識別的局限性，提出了1種利用篩體自由振動響應實現大型振動篩減振彈簧剛度反演的方法。考慮減振系統幾何位置誤差，建立了減振彈簧故障下振動篩非對稱動力學模型，推導其振動微分方程;利用離散加速度自由響應，結合數字濾波、趨勢項消除和數值積分方法，獲取系統剛度矩陣修正形式;在此基礎上，通過剛度矩陣分解，定義剛度置信準則，提出了大型振動篩減振彈簧剛度反演原理與方法;利用實驗測試數據實現了振動篩減振彈簧的剛度反演，最大誤差僅為3．56%，表明了算法的有效性，實現了減振彈簧定量的健康狀態識別。

關鍵詞:振動篩;減振彈簧;剛度反演;健康識別

彭利平，劉初升，王宏．基于剛度反演的大型振動篩減振彈簧健康識別［J］．煤炭學報，2016，41(6):1568－1574．doi:10．13225/j．cnki．jccs．2015．1200

Peng Liping，Liu Chusheng，Wang Hong．Health identification for damping springs of large vibrating screen based on stiffness identification ［J］．Journal of China Coal Society，2016，41(6):1568－1574．doi:10．13225/j．cnki．jccs．2015．1200

選煤是實現煤炭清潔高效利用、節約資源、保護環境的有效方法。篩分作業是選煤的關鍵環節，目前被廣泛應用的篩分設備是振動篩［1－2］。隨著我國大型煤炭基地大型選煤廠、大中型煤礦配套選煤廠和小型煤礦集中礦區群礦選煤廠的建設［3］，處理量大、效率高的大型振動篩(篩面寬度不小于3.6 m、篩分面積不小于20 m2)［4］被廣泛應用。傳統振動篩動力學模型主要是單自由度或兩自由度互不耦合振動系統，實現的前提是4點減振彈簧完全相同［5］。然而，振動篩在激振系統強交變載荷和物料隨機載荷聯合作用下，減振彈簧易疲勞損傷，引發動力學模型的突變，宏觀上將導致篩體運動軌跡變化，影響設備可靠性及效果。

目前對振動篩減振彈簧健康監測方面的報道較少。筆者建立了適合減振彈簧故障下振動篩運動描述的三自由度動力學模型，討論了其對傳統動力學模型的向下兼容性，并基于此實現了振動篩一故障彈簧和一健康彈簧的定位［5］;在此基礎上，又綜合考慮篩面靜平衡和篩面約束條件下的減振彈簧小位移變形協調，建立了定點壓力作用下各彈簧壓縮變形量的計算模型，并推導其計算表達式，通過數值仿真分析各彈簧壓縮變形量與懸掛質量位置的定性關系，推導了定點壓力作用下故障前后彈簧壓縮量變化與彈簧剛度變化的定量關系，提出了利用變形靈敏度系數(DSC)來反映彈簧壓縮量對彈簧剛度變化的靈敏程度，并基于此提出了振動篩減振彈簧故障診斷的2次懸掛質量法［6－7］。上述研究對振動篩減振彈簧健康狀態的評估具有一定的有效性，但是局限于定性判斷，且僅能識別一故障彈簧。若能利用大型振動篩的動力學特性反演計算減振彈簧的有效支撐剛度，并與設計值比較，就能從彈簧剛度數值上定量彈簧健康狀態。

筆者先建立了減振彈簧故障下振動篩非對稱動力學模型，從自由響應出發，實現了振動篩系統剛度矩陣的推導和剛度反演原理的提出，最后將所提原理在實驗室振動篩模型機上進行了彈簧剛度反演的應用測試，證實了其有效性。

1　減振彈簧故障下振動篩非對稱動力學模型

減振彈簧故障下篩體經歷空間復雜運動，筆者給出了減振彈簧故障下的振動篩耦合動力學模型［5］，主要考慮了篩體“浮沉”、“側滾”和“點頭”運動的耦合。由于減振系統幾何位置誤差下4點減振彈簧支撐可能非對稱分布，不失一般性，這里建立彈簧故障下振動篩非對稱動力學模型［8］，如圖1所示。

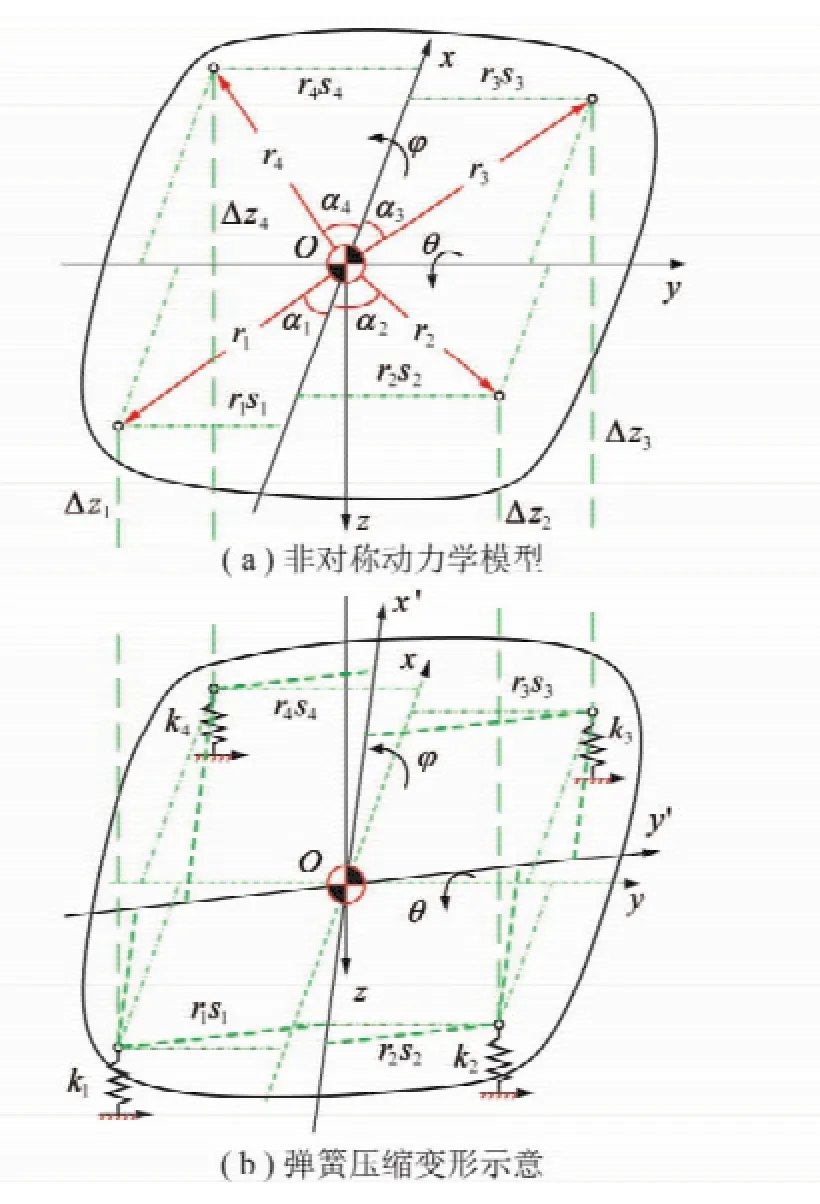
圖1　減振彈簧故障下振動篩非對稱動力學模型及彈簧壓縮變形示意Fig.1　Asymmetric dynamic model of the vibration screen with damping spring fault and sketch for the compressed deformation of damping springs

由于篩體剛度大，激振頻率一般小于篩體彈性變形的基頻，因此自由振動時可忽略其彈性變形。無擾動下靜平衡篩面處于圖1(a)位置;當篩體振動時，某一時刻篩面處于圖1(b)位置。減振彈簧各支點與質心O的位置關系以距離ri和夾角αi(i=1，2，3，4)表示。設篩體質量為m，繞x軸和y軸的轉動慣量分別為Jx和Jy，任意時刻運動量以篩體豎直方向位移z、繞x軸轉動角φ及繞y軸轉動角θ這3個自由度(廣義坐標)表示。

擾動下減振彈簧的豎直壓縮變形量分別為Δz1，Δz2，Δz3和Δz4，以3個廣義坐標的耦合表示為

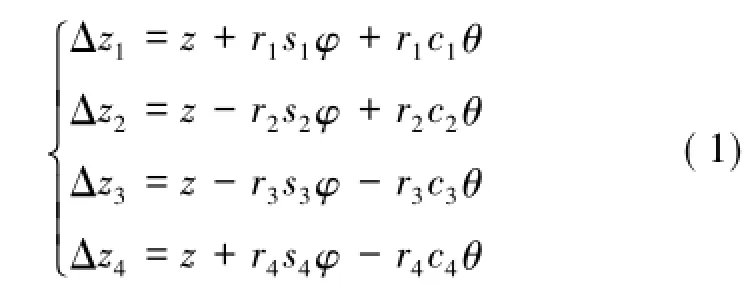
其中，si=sin αi且ci=cos αi(i=1，2，3，4)。由于剛體擺動幅度很小，將sin φ和sin θ利用零值處歐拉公式展開后可分別替代為弧度制下的φ和θ。

為方便計算，將式(1)用矩陣表示

式中，x={z，θ，φ}T為廣義坐標矩陣;T為廣義坐標至減振彈簧豎直壓縮量的映射矩陣，

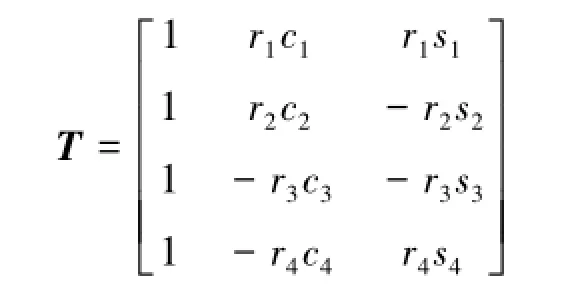
一般地，工程線性系統阻尼往往是看作比例黏性阻尼［9］。基于拉格朗日方程，減振彈簧故障下振動篩比例阻尼系統自由振動微分方程［10］一般表示成:

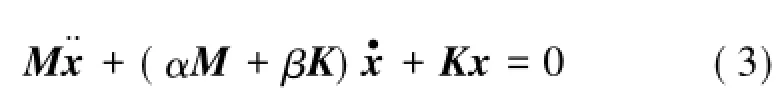
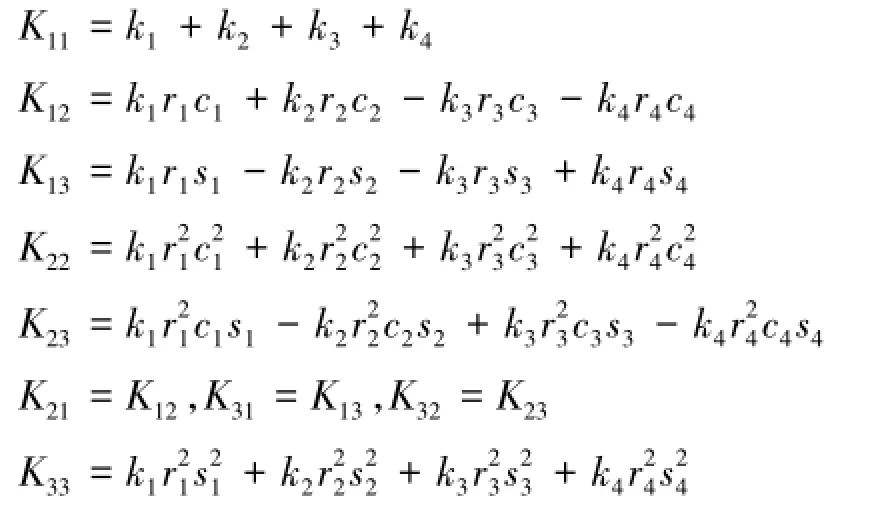
很明顯，由于是線性動力系統，剛度矩陣K為對稱陣，各元素為4點減振彈簧剛度表達式。

2　反演原理

2.1剛度矩陣推導

剛度反演的主要目的是通過篩體自由振動響應反推剛度矩陣中各剛度的數值，式(3)轉化為

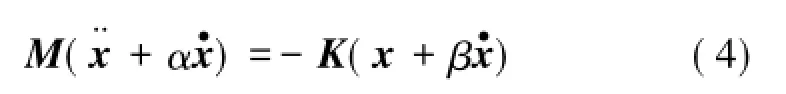
構造矩陣形式的自由振動響應，即位移X3×N= ［xk，xk+1，…，xk+i，…，xk+N－1］，其中，xk+i={x1，k+i，x2，k+i， x3，k+i}T，速度和加速度類似，其中，3為系統自由度數;N為自由振動響應中采用的離散運動量點數;k為截取起始位置;xj，k+i，和分別為第j(j=1，2，3)個自由度在第k+i個離散時刻的位移、速度及加速度。因此，式(4)可以表示成

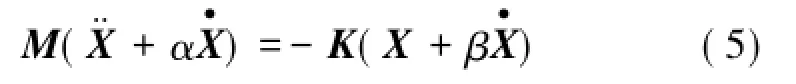
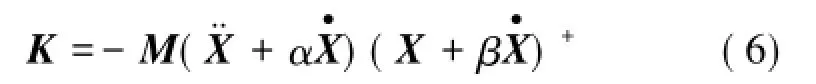
式中，上標“+”表示Moore－Penrose廣義逆陣［12］。

針對圖1的減振彈簧故障下振動篩非對稱動力學模型，由式(2)得

構造各彈簧壓縮量變形位移矩陣 ΔZ=［Δzk，Δzk+1，…，Δzk+i，…，Δzk+N－1］，其中，Δzk+i={Δz1，k+i，Δz2，k+i，Δz3，k+i，Δz4，k+i}T，而變形速度、加速度的矩陣形式依此類推。故有

將式(8)～(10)代入式(6)中，該系統的剛度矩陣滿足:

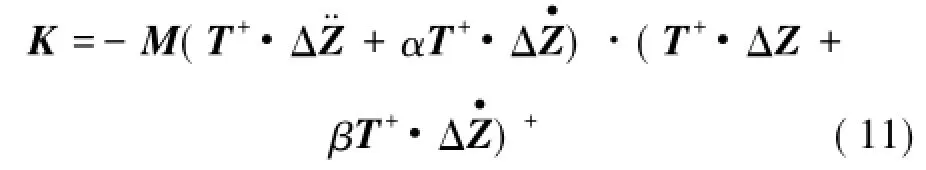
觀察式(4)中各個元素，可以發現，剛度矩陣K的構型與彈簧是否存在損傷無關，因此理論上始終是對稱陣。為使由自由響應矩陣和式(11)計算得到的系統剛度矩陣保持這一特性，這里引入如下數學處理［13］:

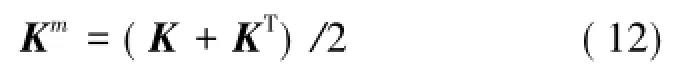
作為剛度矩陣的修正形式Km。

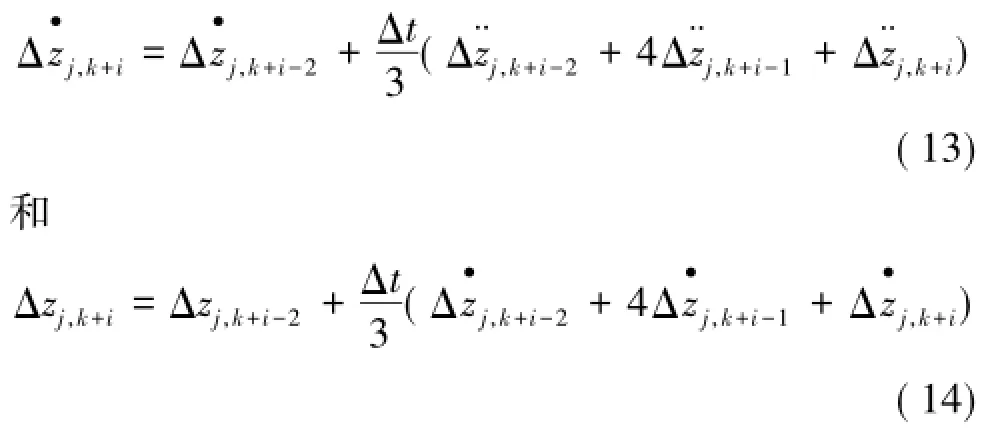
來實現速度及位移的獲取，進而構造反演所需的速度及位移矩陣。其基本流程如下:

(1)鑒于實際加速度信號中的噪聲干擾，利用數字濾波(DF)方法對采樣的數字離散信號進行噪聲剔除，保留有用成分用于構造加速度矩陣及后續數值積分的源信號;

(2)為防止源信號零漂的影響，數值積分后需進行消除趨勢項(ETT)來消除直流項造成的信號偏移失真，使積分信號盡量接近真實;

(3)最后將處理后的信號構造式(6)中的自由振動響應速度及位移矩陣。

整個過程如圖2所示。

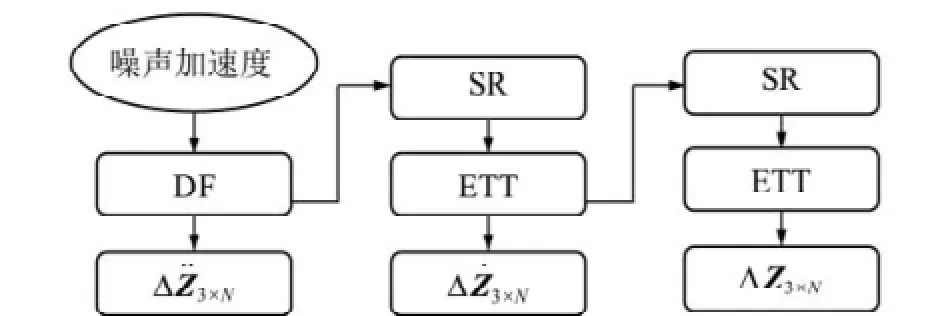
圖2　時域中由加速度計算速度和位移矩陣的數字信號處理Fig.2　Digital signal processing for time-zone acceleration transforming into the corresponding velocity matrix and displacement matrix

2.2反演過程與置信準則

剛度矩陣中各元素是關于各減振彈簧剛度和支點位置的函數，下面研究剛度矩陣已知的情況下進行剛度值反演識別的方法。

定義Km的剛度變形矩陣，滿足［8］

其中，Ae和Kme分別為剛度聯系矩陣和單元剛度變形矩陣。剛度聯系矩陣Ae只與系統彈簧支撐位置有關，彈簧剛度任意組合狀態下Ae保持不變，單元剛度矩陣如下形式:

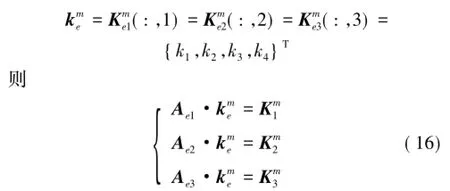
依次展開后得到的方程組中方程個數(3)均少于未知參數(4個剛度值)，為不定方程，因此方程(16)各含有無數組可行解(設為，和)。由于彈簧剛度值確定，故方程組解惟一，惟一解即公共解。采用常規的偽逆解法可分別得到各個方程組的最小范數解，但不能保證各解相同(近)而符合惟一性。為此，這里設計如下數值算法:考慮到方程組惟一解的必然存在性，使某一彈簧的剛度值在一定范圍［kmin，kmax］(其中，kmin取0，kmax取彈簧剛度設計值)內進行循環賦值，以k1為例，對于任意1個數值，代入方程(16)中即可使之降維而獲得惟一可行解(設為和)。為評價這些解的接近程度，類似模態置信準則MAC［14］，定義剛度置信準則:

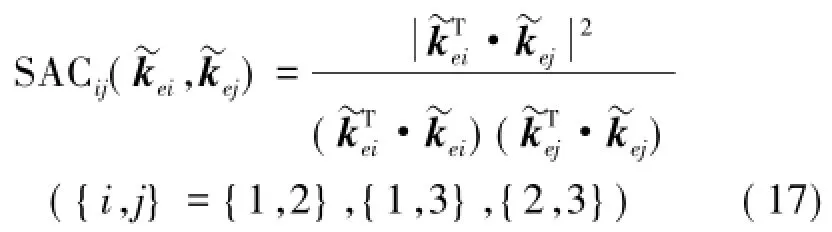
來量化兩反演剛度向量的相關程度，其取值0～1。SAC值趨于 1，表明 2組反演剛度的一致性好;SAC值趨于0，說明2組反演效果不理想。

同時，定義趨向于1的剛度置信準則的閾值S，用于反映反演相關程度要求，獲取所有同時滿足:①SAC12()≥S，② SAC13()≥S和③SAC23()≥S的SAC值所對應的反演剛度向量。若條件①，②和③獲得的反演剛度向量分別為，由于各組剛度向量間的相關程度均很高，因此可以選取6組解的平均值作為方程組(16)的公共解，其各個元素即為剛度反演值{k1，k2，k3，k4}。

3　剛度反演的實驗驗證

文獻［8］通過數值實驗，對上述剛度反演算法的準確性和有效性進行了詳細的說明，其具有如下特征:反演計算所采用的信號起始位置和長度對反演精度沒有影響，而只與截取信號的純凈程度相關;采用的離散運動量點數N越大，一般反演效果越好;DF中帶通數字濾波截止頻率由結構固有頻率決定，帶寬略大于固有頻率的最大差值。

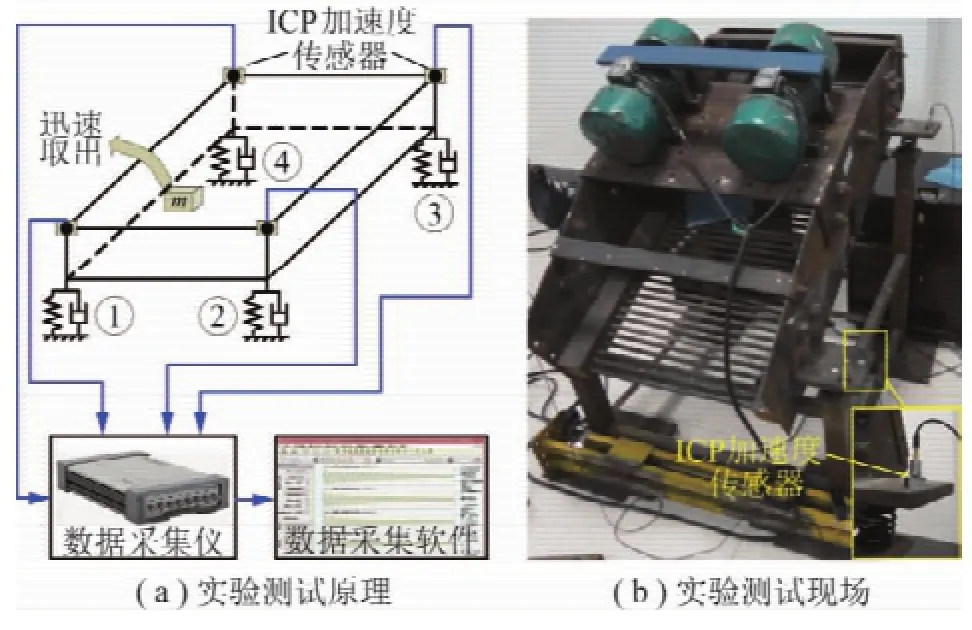
圖3　振動篩減振彈簧剛度反演應用實驗系統及裝置Fig.3　Application test and apparatus for stiffness identification for damping springs of vibrating screen

這里以實驗室振動篩模型機為應用實驗對象來驗證上述基于自由響應的振動篩減振彈簧剛度反演原理的實用性。實驗系統及裝置如圖3所示，將4個ICP加速度傳感器(INV9821，分辨率0.002 m/s2，量程50 g，頻響范圍0.5～8 kHz)通過磁座吸附在篩體各上壓板上方，用于測試減振彈簧豎直壓縮變形量(Δz1，Δz2，Δz3，和Δz4)的變化加速度，加速度傳感器與數據采集儀(INV3060A)相連，通過數據采集軟件(DASP－V10工程版)進行信號采集與處理。

一般情況下，振動篩4點支撐減振彈簧的剛度相同，這里用2組簧絲直徑不同但自由高度相同的彈簧實現振動篩減振彈簧的剛度不同模擬。彈簧參數見表1，由于簧絲直徑尺寸的標準化，選購的模擬故障彈簧有限，其剛度相比初始彈簧，降低約25%。模擬故障彈簧是2號彈簧。

設定系統采樣頻率為1 024 Hz，定時采樣時間為15 s，人為施加脈沖激勵使篩體偏平衡而作自由振動。圖4為振動篩模型機4個彈簧支撐位置處的自由振動響應(加速度)曲線及對應的功率譜密度函數圖，可得到系統的前三階固有頻率分別為4.15，5.05 和6.125 Hz。根據表2中的基本參數，在2號減振彈簧剛度為 32 270 N/m、其他減振彈簧剛度為42 990 N/m的情況下，依據理論模態分析根據各階固有頻率的計算公式=0［9］獲得實驗振動篩的固有頻率計算值分別為4.104 9，4.924 1和6.254 4 Hz。

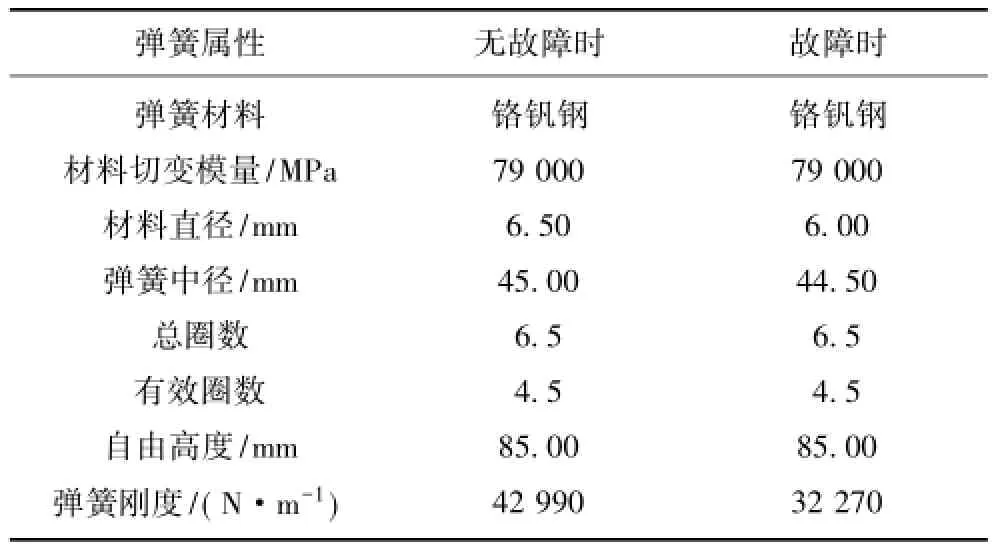
表1　實驗用振動篩無故障和故障彈簧的基本參數Table 1　Fundamental parameters of the healthy and the fault springs of the experimental vibrating screen

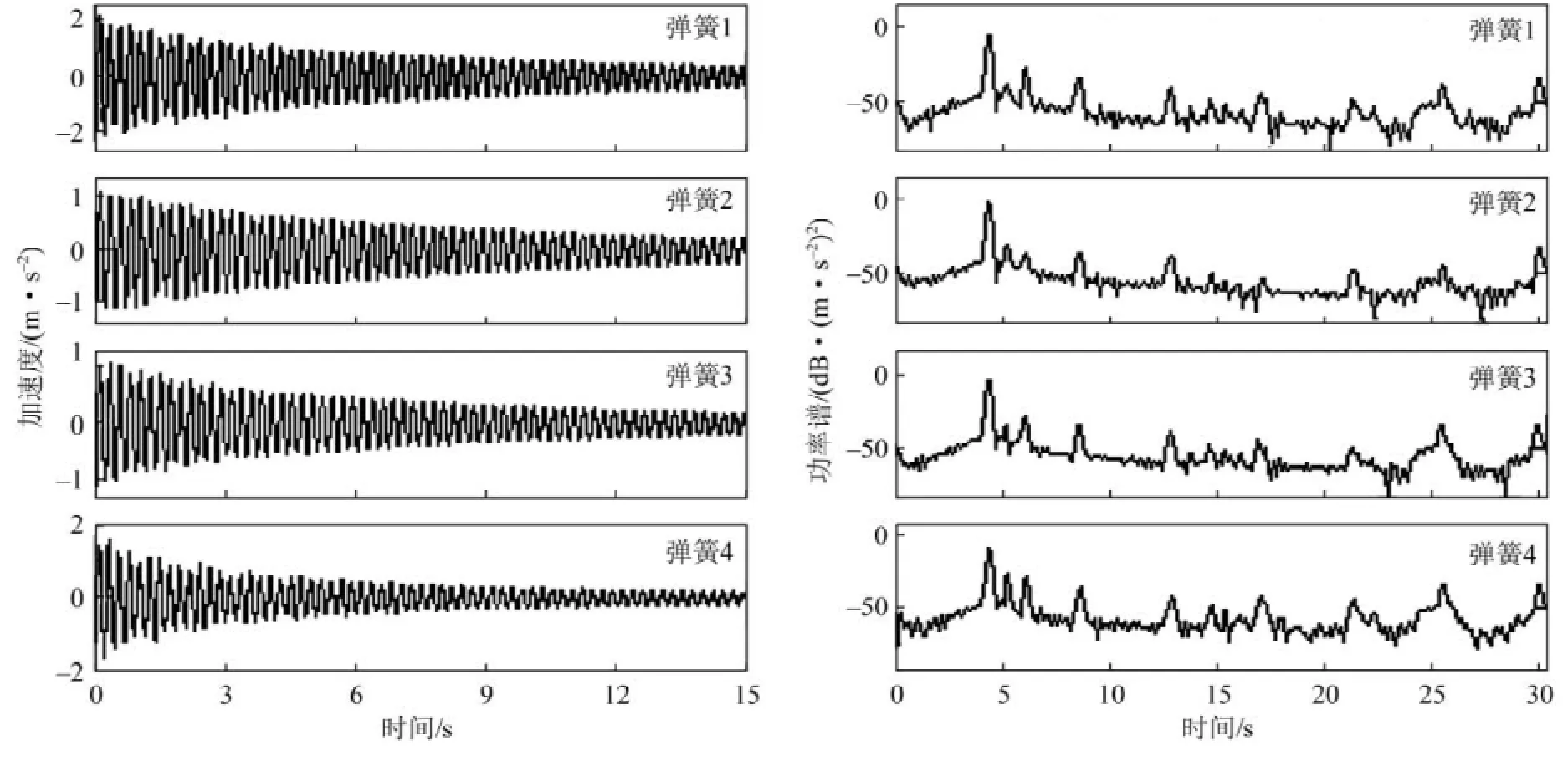
圖4　單個彈簧(No.2)故障時的自由響應曲線及功率譜Fig.4　History of the free response of each plate pressured on spring No.1－4 and the corresponding power spectrum with single spring No.2 fault

表2　實驗用振動篩的基本參數Table 2　Fundamental parameters of the experimental vibrating screen

將采集的各個彈簧位置處的篩體自由振動加速度信號，按圖2所示的時域中噪聲加速度計算速度和位移的數字信號處理過程，進行濾波、積分和去趨勢項等操作，如圖5所示。加速度、速度和位移隨時間遞減，且計算所得速度(圖5(c))和計算所得位移(圖5(e))在去趨勢前后均有明顯的信號基準的移動，即零漂消除。

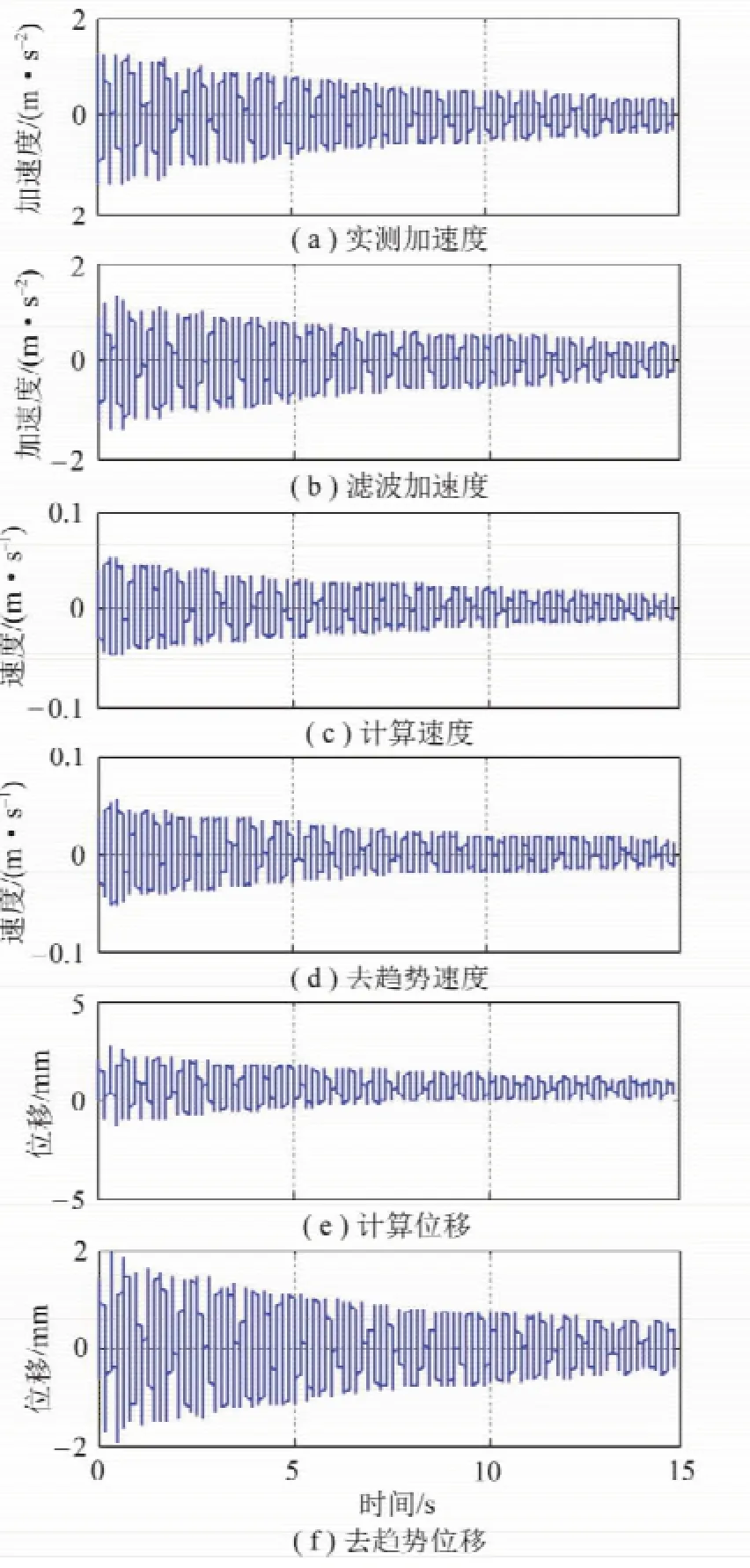
圖5　彈簧2故障時的彈簧1處的實測加速度、濾波加速度、計算速度、去趨勢速度、計算位移和去趨勢位移Fig.5　Free response of spring No.1 with No.2 fault:original acceleration，filtered acceleration，calculated velocity，trendeliminated velocity，calculated displacement and trend-eliminated displacement

結合系統參數(表1，2)，將所示方法處理后的位移、速度和加速度構成自由響應矩陣，根據反演原理得到反演的剛度值。進行4次重復實驗，其中，第1次實驗k1變化時剛度置信準則變化歷程如圖6所示，選用的相關參數為:N=8 000，［fu，fd］=［1.00， 20.00］，∈［38.00，47.00］，對應的剛度置信閾值均定為S=0.999 5。

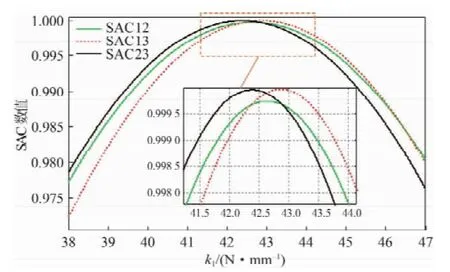
圖6　k1變化時剛度置信準則變化歷程Fig.6　History of the stiffness assurance criterion with the variable stiffness value of spring No.1

4次實驗中，人為隨機按壓篩體不同位置使之作自由振動，通過提出的反演算法，得到的反演結果列于表3中。很明顯，定性來看，2號彈簧故障最嚴重，與文獻［5］的診斷結果一致;定量來看，反演效果均比較理想，與設計值的最大誤差僅為3.56%，驗證了算法的可行性及穩定性。因此，可以認為基于自由響應的振動篩減振彈簧剛度反演可以實現振動篩各個減振彈簧剛度的定量，進而與設計值進行比較，診斷彈簧狀態。

4　結　　論

(1)建立了減振彈簧故障下振動篩非對稱動力學模型，推導了減振系統幾何位置誤差下振動篩空間三自由度運動的振動微分方程。

(2)提出了利用加速度響應獲取速度、位移響應的數字信號處理方法，構造系統的響應矩陣，開發了減振彈簧剛度反演基本原理與方法，實現了篩體自由響應反推出各減振彈簧剛度。

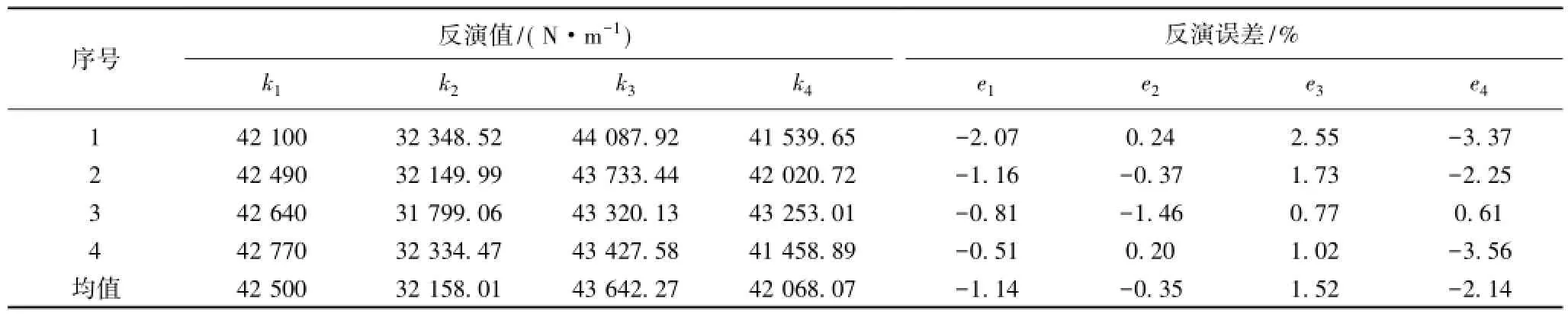
表3　實驗獲得的剛度反演結果Table 3　Stiffness identification results based on the experiment

(3)研究結果對大型振動篩減振彈簧健康識別及保障設備運行可靠性具有一定的應用價值。

參考文獻:

［1］劉初升，蔣小偉，張士民，等．變軌跡等厚篩振動方向角的計算及實驗驗證［J］．中國礦業大學學報，2011，40(5):737－742．Liu Chusheng，Jiang Xiaowei，Zhang Shimin，et al．Calculation and experimental verification of vibrating direction angle of varying trajectory banana screen［J］．Journal of China University of Mining＆Technology，2011，40(5):737－742．

［2］Zhao Yuemin，Liu Jiongtian，Wei Xianyong，et al．New progress in the processing and efficient utilization of coal［J］．Mining Science and Technology，2011，21(4):547－552．

［3］國家能源局．關于促進煤炭工業科學發展的指導意見［EB/ OL］．http://www．nea．gov．cn/2015－03/25/c_134095304．htm，2015－03－25．

［4］Zhao Yuemin，Liu Chusheng，Li Fengming，et al．Dynamic analysis and optimization of a large-scale vibrating screen with high reliability［A］．XXVIIInternational Mineral Processing Congress(IMPC2014)，2014 ［C］．Chile，Santiago:Gecamin Digital Publications，2014:116－124．

［5］劉初升，彭利平，王宏，等．大型振動篩彈簧故障識別的自由響應法［J］．振動工程學報，2013，26(4):624－632．Liu Chusheng，Peng Liping，Wang Hong，et al．Fault identification for spring of large vibrating screen using free response［J］．Journal of Vibration Engineering，2013，26(4):624－632．

［6］Peng Liping，Liu Chusheng，Li Jun，et al．Static-deformation based fault diagnosis for damping spring of large vibrating screen［J］．Journal of Central South University，2014，21(4):1313－1321．

［7］劉初升，彭利平，趙躍民，等．振動篩減振彈簧故障診斷方法［P］．中國專利:ZL201310134768，2015－04－15．Liu Chusheng，Peng Liping，Zhao Yuemin，et al．Fault diagnosis method for damping springs of vibrating screen［P］．China Patent:ZL201310134768，2015－04－15．

［8］Peng Liping，Liu Chusheng，Wu Jida，et al．Stiffness identification of four-point-elastic-support rigid plate［J］．Journal of Central South University，2015，22(1):159－167．

［9］J．H．金斯伯格．機械與結構振動——理論與應用［M］．白化同，李俊寶，譯．北京:中國宇航出版社，2005．

［10］彭利平．大型振動篩減振彈簧剛度反演及梁體動力學問題研究［D］．徐州:中國礦業大學，2015．Peng Liping．Study on stiffness identification for damping springs and dynamic problems of beam structures in a large vibrating screen ［D］．Xuzhou:China University of Mining and Technology，2015．

［11］Wang B T，Cheng D K．Modal analysis by free vibration response only for discrete and continuous systems［J］．Journal of Sound and Vibration，2011，330(16):3913－3929．

［12］Yang Q W，Sun B X．Structural damage identification based on best achievable flexibility change［J］．Applied Mathematical Modelling，2011，35(10):5217－5224．

［13］董聰．現代結構系統可靠性理論及應用［M］．北京:科學出版社，2001．

［14］Pastor M，Binda M，Harˇaarik T．Modal assurance criterion［J］．Procedia Engineering，2012，48:543－548．

中圖分類號:TD452;TH135

文獻標志碼:A

文章編號:0253－9993(2016)06－1568－07

收稿日期:2015－08－14修回日期:2015－10－12責任編輯:許書閣

基金項目:國家自然科學基金資助項目(51221462);中央高校基本科研業務費專項資金資助項目(2015B30214);中國博士后科學基金面上資助項目(2016M590514)

作者簡介:彭利平(1987—)，男，江蘇江陰人，講師，博士。E－mail:plpbeckham@163．com

Health identification for damping springs of large vibrating screen based on stiffness identification

PENG Li-ping1，LIU Chu-sheng2，WANG Hong3
(1．College of Mechanical and Electrical Engineering，Hohai University，Changzhou213022，China;2．School of Mechatronic Engineering，China University of Mining and Technology，Xuzhou221116，China;3．Tangshan Research Institute，China Coal Technology and Engineering Group Corp．，Tangshan063012，China)

Abstract:In order to overcome the limitation of qualitatively health identification for damping springs of large vibrating screen(LVS)，a diagnostic methodology for identifying the stiffness of damping springs with free response was proposed．With the geometric position error of the damping system considered，the asymmetric dynamic model of the vibration screen with damping spring fault was established and followed by deriving the vibration differential equation．Then，the discrete free acceleration response data were processed by digital filter，eliminating the trend item and numerical integration，and subsequently constructed in a matrix form to obtain the modified stiffness matrix．Moreover，with disassembling stiffness matrix and defining the stiffness assurance criterion，the principle and procedures for stiffness identification of a large vibrating screen was summarized．Finally，the validity of the developed method for stiffness identification was verified by an experimental test and the error is within 3．56%．The research may accomplish the quantitatively health identification for the damping springs of large vibrating screen．

Key words:vibrating screen;damping spring;stiffness identification;health identification