基于T90分布的BeppoSAX衛星伽瑪暴分類研究

楊恩波

（貴州大學理學院，貴州　貴陽　550025）

?

基于T90分布的BeppoSAX衛星伽瑪暴分類研究

楊恩波

（貴州大學理學院，貴州貴陽550025）

摘要：伽瑪暴的分類是伽瑪暴相關研究中的熱點問題之一，目前被廣泛接受的方法是基于伽瑪暴持續時間的分類方法。本文采用高斯混合模型和最大期望算法對BeppoSAX衛星軌運行期間所探測到的694個伽瑪暴持續時間的概率密度分布進行了研究，同時利用貝葉斯信息準則對不同的模型進行了比較。分析結果支持雙高斯成分的模型比其他模型更好地描述了BeppoSAX衛星所探測到的伽瑪暴持續時間的分布，同時這一結論與其他衛星數據的分析結果一致，均支持存在兩種類型的伽瑪暴。

關鍵詞：伽瑪暴；持續時間；數據分析

伽瑪射線暴(Gamma Ray Burst,GRB)，又稱伽瑪暴，是來自天空中某一方向的伽瑪射線強度在短時間內突然增強，隨后又迅速減弱的現象。伽瑪暴是當今天文學上最活躍的前沿領域之一。

宇宙中充滿著各種強烈的爆發現象，如超新星爆炸等，伽瑪暴是其中一種極其強烈的恒星級的爆發現象，最初由美國的Vela軍事衛星在1967年探測到。初期由于缺乏足夠的觀測數據，相關的研究工作進展緩慢。1991年，美國成功發射康普頓天文臺，其在隨后接近10年的成功運行中取得了大量伽瑪暴觀測數據，為研究人員對伽瑪暴展開各方面研究提供了充足的觀測依據，如何對伽瑪暴進行分類是伽瑪暴研究熱點之一。目前被廣泛接受的分類法是基于持續時間T90（探測器探測到的輻射本底以上光子積分流量從5%增長到95%所用時間）的長短進行的，這一方法由Kouveliotou等在1993年首次提出［1］，他們統計了BATSE樣本庫中的222個伽瑪暴持續時間T90的分布，發現logT90的分布中存在兩個峰，基于這一發現，他們提出長短暴的分類方法，即以T90= 2.0s為界限，可以分為兩類，長暴（LGRBs）和短暴（SGRBs），其中長暴約占75%，短暴約占25%。這兩類伽瑪暴被認為具有不同的物理起源。短暴被認為是雙致密星互相纏繞后的產物［2］，如雙中子星系統或者一顆中子星伴隨一顆黑洞，而長暴則被認為與大質量恒星的爆炸有著密切的聯系［3］。

Horváth［4］通過分析BATSE樣本庫中的797個伽瑪暴的logT90分布發現了第三種伽瑪暴存在的證據，類似的證據同樣在BeppoSAX衛星數據［5］、Swift衛星數據［6］及Fermi衛星數據［7］中被發現。需要注意的是，類似的工作在進行數據分析時所采用的方法通常是對logT90做直方圖，然后對直方圖進行高斯擬合并利用卡方檢驗判斷擬合結果優劣。這一方法的結果不可避免地會受到直方圖的bin過程影響，不同大小的bin最終會導致不同的分析結果。在該文中，將采用高斯混合模型（Gaussian Mixture Model，GMM）和最大期望算法（Expectation and Maximization Algorithm）重新對BeppoSAX衛星探測到的伽瑪暴的持續時間分布進行研究，從而避免受bin大小的影響。

1　樣本選取及分析方法

1.1樣本選取

BeppoSAX衛星由意大利和荷蘭共同研發，其搭載的寬視場相機（Wide Field Camera，WFC）和Phoswich探測器（Phoswich Detector System，PDS）聯合工作可以有效地對伽瑪暴進行探測并確定其位置。BeppoSAX在伽瑪暴研究領域的最突出貢獻是確認了伽瑪暴的河外起源［8］。為了對BeppoSAX衛星所探測到的伽瑪暴進行logT90的概率密度分析，從BeppoSAX衛星伽瑪暴樣本庫（http:// heasarc.gsfc.nasa.gov/W3Browse/gamma-ray-bursts/saxgrb?mgrb.html）中的1 082個伽瑪暴中選取了694個具有代表性的伽瑪暴作為樣本，它們均擁有有效的持續時間信息和能譜參數信息。

1.2分析方法

GMM是參數化的概率方程，通過不同權重的高斯成分疊加組成，在進行一維數據的概率密度分析時，樣本整體的似然值可以表示為：

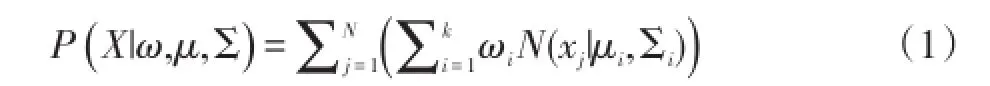
其中，N代表樣本的個體總數；X代表所選取的樣本集合；ωi、μi、Σi分別代表第i個高斯成分的權重，中心值和相關矩陣；N(xj|μi,Σi)代表第i個高斯成分的概率密度，其計算方法為：

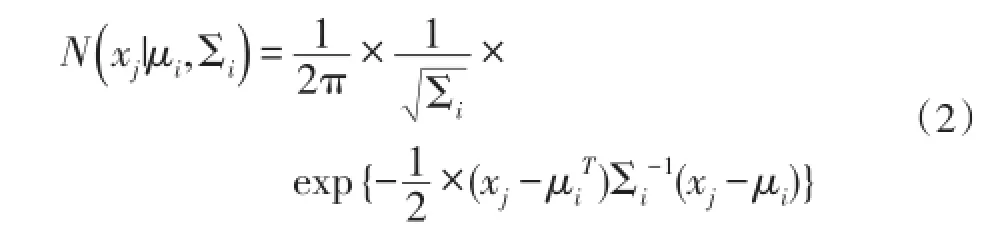
在指定高斯成分個數k后，最佳的模型參數將通過EM算法獲得。EM算法將通過不斷的在（a）和（b）之間進行迭代，獲得最P（X∣ω、μ、Σ）值的參數便是最佳參數，相應的模型便是k個高斯成分下的最佳模型。

（a）估計未知參數ωi、μi、Σi的期望值，給出其參數估計。

（b）重新估計分布參數，以使得數據的P（X∣ω、μ、Σ）最大，給出ωi、μi、Σi的期望估計。

貝葉斯信息準則（Bayesian Information Criterion，BIC）可用于比較不同高斯成分個數下最佳模型的對待分析樣本的適應程度，即決定高斯成分的個數［9，10］。BIC的計算方法為：

其中，N代表樣本中個體數目，p和Pmax分別代表待考察模型的參數個數及該模型的最大似然值。BIC值最小的模型便是最適應樣本的模型。對于其他模型，如果其BIC值超過最小值0～2，則其同樣可適應樣本；如果超過最小值2～6，則其對樣本的適應度將變弱；若超過最值6以上，則其對樣本的適應度明顯下降，可以被排斥掉［11］。

2　結果分析

具有2個高斯成分的GMM模型（2-G）和3個高斯成分的GMM模型（3-G）分別被用于分析BeppoSAX衛星伽瑪暴持續時間的概率密度分布，具體分析結果見圖1和圖2，兩圖中均加入背景直方圖方便比較GMM模型輸出結果，直方圖的bin符合Knuth規則［12］。各自最佳的參數見表1。

從圖1和圖2、表1中可以看出，2-G模型的表現要好于3-G模型，二者的BIC值分別為1 255.351和1 274.951，3-G模型的BIC值已經超過2-G模型的數值接近20，遠大于足以導致其被排斥的6，這說明對于Bep?poSAX衛星伽瑪暴持續時間的分布，2-G模型的適應程度要更好，3-G模型的表象遠不如2-G模型，是被強烈排斥的，這一結果與Yang等［13］利用相同方法分析的Fermi衛星數據結論一致，與Zhang和Choi對Swift衛星數據的分析也是一致的。

對于最佳的2-G模型，兩個高斯成分的比例為0.253∶0.747，與Kouveliotou等［1］得到的0.250∶0.750的比例十分接近。但是由圖1可見，兩個高斯成分的則大于2.0s，同時兩個高斯成分相互交錯的區域較大，考慮到該文選取的是BeppoSAX衛星探測到的伽瑪暴，Kouveliotou等［1］分析的樣本來自BATSE，兩種樣本可能會受到探測器選擇效應影響，導致最終的結果存在差異［2］。

為了確定是否更多高斯成分的模型比2-G模型表現更好，利用相同的方法，對高斯成分個數從1到9共9個模型均做了進一步分析，相應的BIC值比較如圖3所示，可見2-G模型的BIC值位于最低點，其余模型對于Bep?poSAX衛星伽瑪暴持續時間概率密度分布的適應程度都要差于2-G模型。

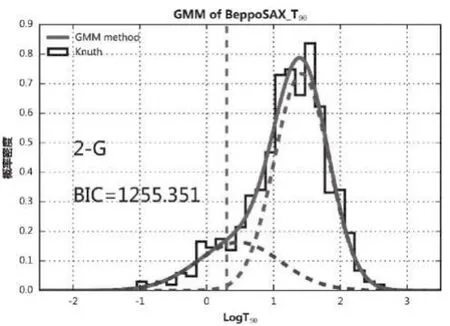
圖1 2-G模型輸出結果

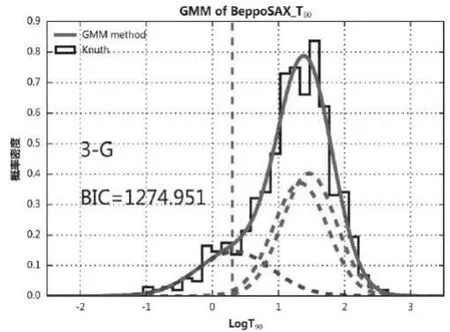
圖2 3-G模型輸出結果

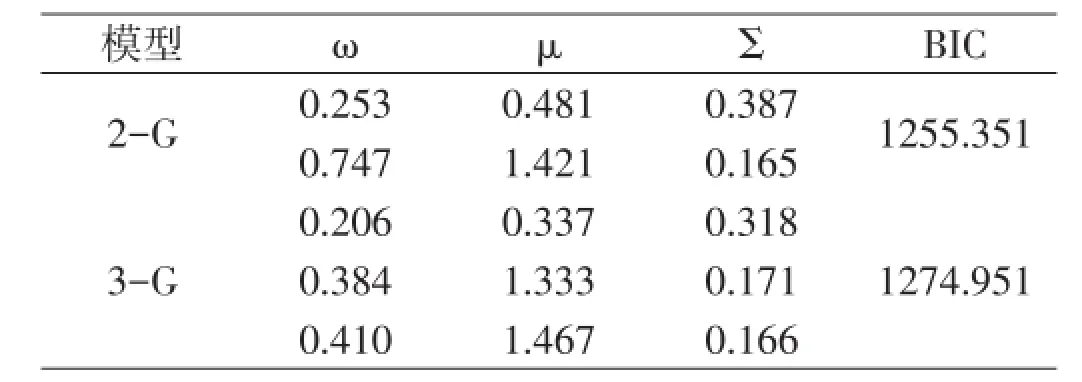
表1 2-G模型和3-G模型的輸出參數及BIC值

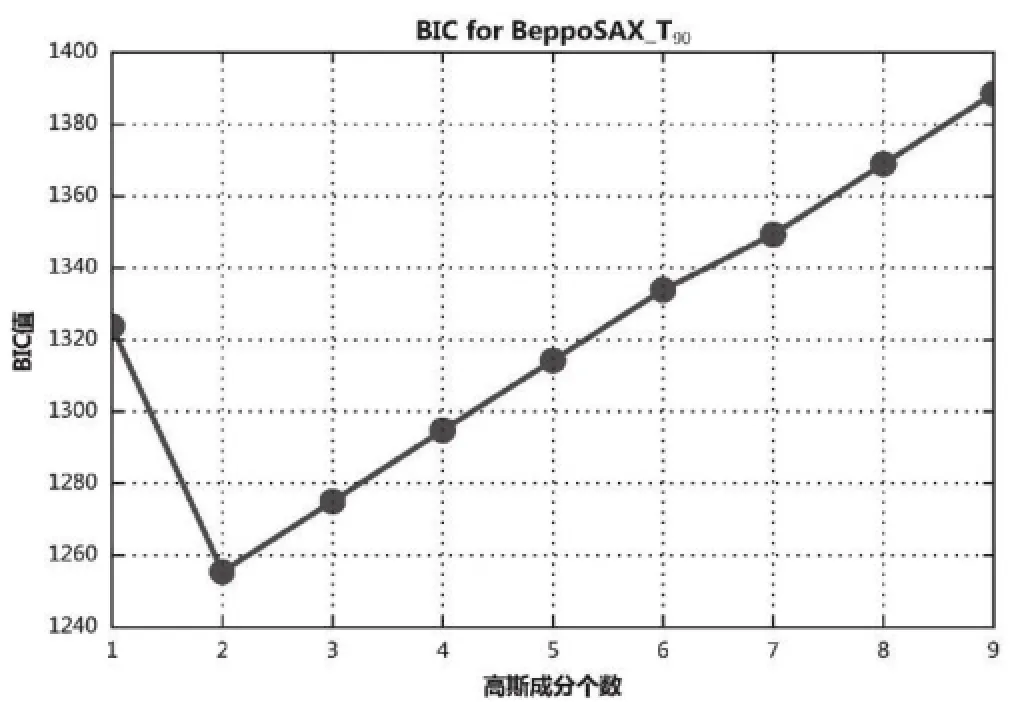
圖3 不同高斯成分個數的模型BIC值比較

3　小結

持續時間的分布是對伽瑪暴進行分類的依據之一，該文利用高斯混合模型及最大期望算法，對BeppoSAX衛星探測到的694個伽瑪暴持續時間進行了概率密度分布研究，避免了常用的擬合直方圖方法受bin過程影響。分析結果顯示，BeppoSAX衛星伽瑪暴的持續時間仍然服從雙模分布，2個高斯成分組成模型能夠更好地描述該分布，這一結論支持已經被廣泛接受的長短暴分類方法，同時與其他衛星數據的分析結果一致。

參考文獻：

［1］Kouveliotou C，Meegan C A，Fishman G J，et al.Iden?tification of Two Classes of Gamma-Ray Bursts［J］.The Astro?physical Journal，1993（413）：L101-L104.

［2］Nakar E.Short-Hard Gamma-Ray Bursts［J］.Physics Reports，2007（1）：166-236.

［3］WoosleyS，BloomJ.TheSupernova-Gamma-Ray BurstConnection［J］.Annu.Rev.Astron.Astrophys.，2006 （44）：507-556.

［4］Horváth I.A Third Class of Gamma-Ray Bursts?［J］. The Astrophysical Journal，1998（2）：757.

［5］Horváth I.Classification of BeppoSAX’s Gamma-Ray Bursts［J］.Astrophysics and Space Science，2009（1）：83-86.

［6］Horváth I，Balázs L G，Bagoly Z，et al.Classification of Swift’s Gamma-Ray Bursts［J］.Astronomy&Astrophysics，2008（1）：L1–L4.

［7］Tarnopolski M.Analysis of Fermi Gamma-Ray Burst DurationDistribution［J］.Astronomy&Astrophysics，2015 （581）：A29.

［8］Metzger M，Djorgovski S，Kulkarni S，et al.Spectral Constraints on the Redshift of the Optical Counterpart to the Gamma-Ray Burst of 8 May 1997［J］.Nature，1997（387）：878-880.

［9］Schwarz G.Estimating the Dimension of a Model［J］. The annals of statistics，1978（2）：461.

［10］Liddle A R.Information Criteria for Astrophysical Model Selection［J］.Monthly Notices of the Royal Astronomi?cal Society：Letters，2007（1）：L74–L78.

［11］Burnham K P，Anderson D R.Multimodel Inference Understanding AIC and BIC in Model Selection［J］.Sociologi?cal methods&research，2004（2）：261-304.

［12］Knuth K H.Optimal Data-Based Binning for Histo?grams［J］.arXiv preprint physics，2006.

［13］Yang E B，Zhang Z B，Choi C S，et al.Classifying Gamma-Ray Bursts with Gaussian Mixture Model［J］.arXiv preprint arXiv，2016.

中圖分類號：P172.3

文獻標識碼：A

文章編號：1003-5168（2016）02-0155-03

收稿日期：2016-01-28

作者簡介：楊恩波（1990-），男，碩士，研究方向：理論物理。

Classification of BeppoSAX Satellite Gamma Bursts Based on T90 Distribution

Yang Enbo
（College of Science，Guizhou University，Guiyang Guizhou 550025）

Abstract:Classification of Gamma-ray Bursts(GRB)is very important in GRB studies,the commonly accept?ed method is duration-based method.This paper has done a density probability distribution analysis of 694 GRBs detected by BeppoSAX during it’s operation by using Gaussian Mixture Model and Expectation Maxi?mization Algorithm.Bayesian Information Criterion has been used to compare between different GMM mod?els.The analysis supported that two Gaussian components model performs was better than other models in describing the duration distribution of BeppoSAX GRBs,which was consistent with the results of other satel?lites’data,they all supported the 2-type classification of GRBs.

Keywords:Gamma-ray Burst；duration；data analysis