基于干擾觀測器的飛行器再入姿態廣義預測控制

孫 光 朱如意 王 征

中國運載火箭技術研究院研究發展中心，北京100076

?

基于干擾觀測器的飛行器再入姿態廣義預測控制

孫 光 朱如意 王 征

中國運載火箭技術研究院研究發展中心，北京100076

考慮飛行器模型中的不確定和干擾失配問題，針對再入飛行器提出了一種基于非線性干擾觀測器的廣義預測控制方法。首先，在姿態子系統中引入虛擬廣義預測控制，通過非線性觀測器實現對控制器中未知干擾的估計；其次，對姿態角速度子系統利用廣義預測控制方法進行實際控制輸入設計時，為簡化計算，將虛擬控制的導數作為不確定項同未知干擾一起利用非線性干擾觀測器進行了估計；最后，基于Lyapunov理論證明了飛行器姿態收斂到期望姿態的有界小鄰域內。仿真結果驗證了此方法的有效性。 關鍵詞 再入飛行器；干擾觀測器；廣義預測控制

再入飛行器再入返回過程中飛行軌跡涵蓋外層空間、稀薄大氣層以及稠密大氣層，飛行速度從亞音速、超音速到高超音速甚至接近軌道速度，如此大跨度的飛行范圍使其模型特性變化顯著。另外，各通道間氣動耦合、慣性耦合、運動學耦合嚴重及各種不確定性外部擾動、建模誤差和系統參數不確定的存在，導致姿態控制變得異常復雜。為保證飛行器飛行控制的性能，必須有效抑制上述復合干擾的影響。

預測控制能有效克服受控對象的模型不確定性，并表現出良好的控制性能而得到廣泛的應用，其應用范圍已從最初的工業生產延伸至航空航天領域[1-3]。文獻[4]采用模型預測控制對升力體再入飛行器系統進行了反饋線性化設計。文獻[5]針對具有強耦合、強非線性控制輸入約束的高超聲速飛行器縱向彈性模型, 采用滾動時域H∞優化控制設計了魯棒模型預測控制器，有效抑制了參數不確定和彈性模態的影響。近年來，對具有封閉解析形式的非線性廣義預測控制律的研究引起了很大關注。文獻[6]應用廣義預測方法研究了空天飛行器的姿態控制，取得了很好的效果。文獻[7-8]結合模糊控制理論，針對受模型不確定性和外界干擾的航天器系統將姿態跟蹤加速度誤差引入性能指標，設計了廣義預測控制器，同時利用模糊邏輯系統對模型不確定性和外部干擾進行了逼近，效果較好。

為了保證干擾對控制系統的穩定性能，近幾年，出現了許多關于干擾觀測器的控制方法。當系統模型中干擾相對階不大于控制相對階時，針對再入飛行器魯棒姿態控制問題，文獻[9]提出了一種基于高階滑模觀測器的自適應時變滑模控制器設計方法。文獻[10]設計了一種基于擾動觀測器的全局魯棒的指數時變滑模姿態控制器，實現了精確的姿態控制。文獻[11]基于模糊自適應干擾觀測器設計輸出反饋控制器，解決了具有慣性參數不確定性與外界干擾的自由漂浮空間機械臂的魯棒跟蹤控制問題。當系統模型中存在干擾失配(干擾相對階小于控制相對階)時，文獻[12]采用一種非線性干擾觀測器和反饋線性化相結合的控制方法實現了永磁同步電機系統的輸入輸出線性化。文獻[13]針對包含多源干擾的非線性導彈系統，提出了一種基于非線性干擾觀測器的指令濾波反步控制方法。文獻[14]針對高超音速飛行器這一非線性MIMO系統，采用超扭曲算法設計干擾觀測器，提出一種魯棒反步控制方法，實現了觀測誤差的有限時間收斂。文獻[15]針對導彈的末端制導問題設計了非奇異末端滑模控制與有限時間干擾觀測器，很好的保證了干擾抑制性能。

本文借鑒以上2種方法，針對再入飛行器不確定非線性MIMO系統，提出一種基于非線性干擾觀測器的廣義預測控制方法。設計過程中，充分考慮模型中的干擾失配問題，分別針對姿態子系統和姿態角速度子系統設計了非線性干擾觀測器和廣義預測控制器，較好地處理了模型不確定和干擾失配問題，通過仿真驗證了所設計控制器的有效性。

1 飛行器再入模型

1.1 三自由度質心平動模型

考慮地球自轉對再入運動的影響，將飛行器視作質點，則三自由度質心平動方程[16]可寫為：

(1)

(2)

式中，re，φ，θ分別表示飛行器飛行過程中所處的地心矩、經度和緯度；υ，χ，γ分別表示飛行速度、航向角和航跡角；g0為地球引力常數，ΩE為地球自轉角速度；L，D，Y分別表示飛行器再入過程中受到的升力、阻力和側力。

1.2 三自由度質心轉動模型

繞質心運動的三自由度轉動方程為：

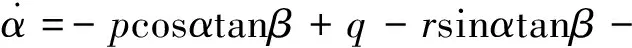
φsinχ)+

(cosφcosχsinγ-sinφcosγ))

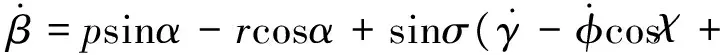
φ

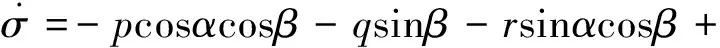
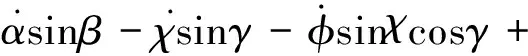
φcosχsinγ+sinφcosγ)

(3)

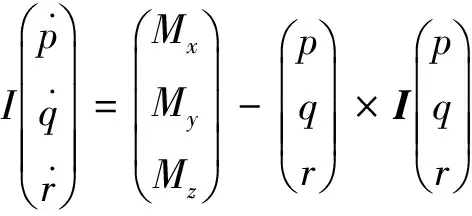
(4)

式中，α，β，σ分別表示攻角、側滑角和傾斜角；p，q，r分別表示滾轉角速度、俯仰角速度和偏航角速度；Mx，My，Mz分別表示滾轉、俯仰和偏航通道的控制力矩；I為飛行器的轉動慣量。

1.3 面向姿控設計的飛行器模型

由以上模型可以看出，質心轉動方程與質心平動方程之間耦合嚴重，不便于控制器設計。為簡化控制器設計，這里將質心平動對轉動的影響作為不確定處理，建立面向姿控設計的飛行器模型：

(5)

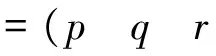
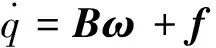
(6)

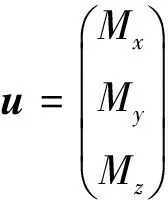
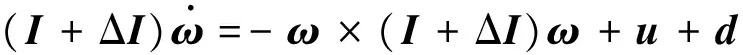
(7)

將式(7)整理可得

(8)

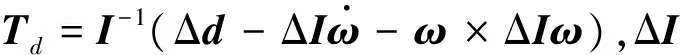
2 基于干擾觀測器的廣義預測控制

本文的控制目標是：考慮面向姿控設計的飛行器模型式(6)和(8)，當存在模型不確定性和外界干擾力矩時，設計控制器使飛行器姿態α,β,σ跟蹤期望的姿態αr,βr,σr，即

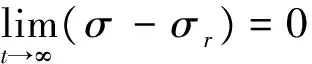
對于面向姿控設計的飛行器模型式(6)和(8)，帶有干擾觀測器的廣義預測控制器的設計思路包括：1)將姿態運動方程作為第1個子系統，設計虛擬廣義預測控制輸入，在此基礎上對控制器中的不確定設計觀測器進行估計和補償；2)將姿態角速度動力學方程作為第2個子系統，設計廣義預測控制輸入，即整個被控系統的真實輸入，同樣在此基礎上對控制器中的不確定設計觀測器進行估計和補償。以下給出帶有干擾觀測器的廣義預測控制器的具體設計過程。

2.1 姿態子系統控制器設計

2.1.1 姿態子系統的預測控制器設計

這里通過設計控制律使以下優化性能指標

(9)

應用Taylor公式，t+τ時刻的姿態q(t+τ)及其導數的預測值可近似寫為：

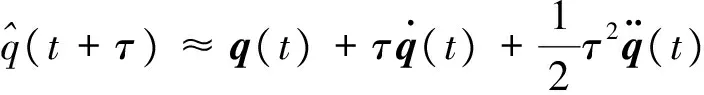
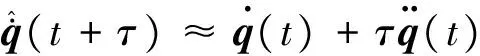
(10)

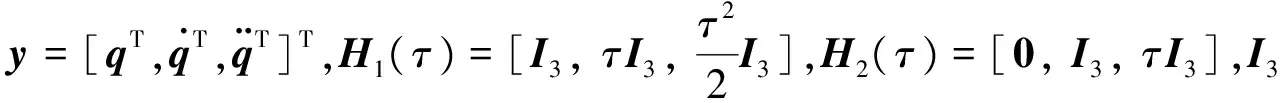
同理，t+τ時刻的期望參考姿態qr(t+τ)及其導數的預測值可近似表示為：

(11)

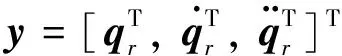
(12)

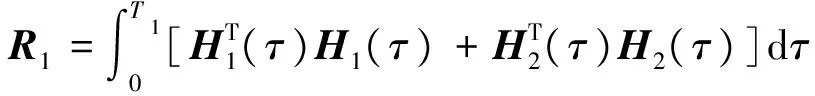
定義姿態角跟蹤誤差及姿態角速度誤差為：

(13)

(14)

其中，ωd(t)為待設計的虛擬控制輸入，qr(t)=[αr,βr,σr]T。

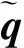
(15)

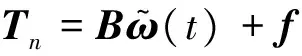
(16)

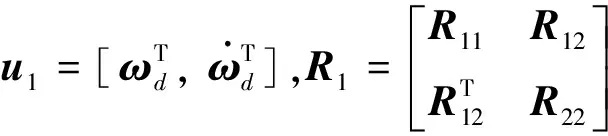
(17)

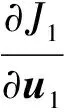
(18)

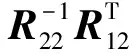
(19)

根據定義可以計算出

定理1 對于飛行器姿態子系統式(6)，在形如式(19)的虛擬控制作用下，閉環系統是全局漸近穩定的。

證明 結合式(13)和(14)，將虛擬預測控制律式(19)代入飛行器姿態運動學方程式(6)，可得閉環系統方程為：

(20)

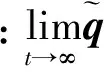
2.1.2 姿態子系統的干擾觀測器設計

上述虛擬控制律中包含有未知項，因此無法執行。這里對Tn作如下假設對其進行非線性觀測器設計。

(21)

對于系統式(21)中的不確定項Tn，設計非線性干擾觀測器為：

(22)

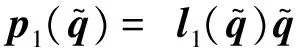
(23)

2.1.3 姿態子系統的基于干擾觀測器的廣義預測控制

設計如下帶有干擾觀測器的虛擬控制

(24)

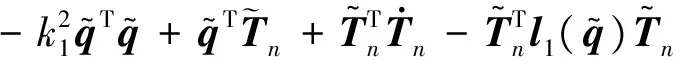
(25)

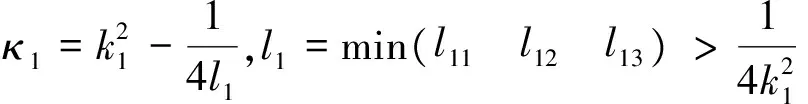
2.2 姿態角速度子系統的控制器設計

2.2.1 姿態角速度子系統的預測控制器設計

基于姿態角子系統控制器的設計，以下進行姿態角速度子系統的實際控制器設計。

這里通過設計控制律使以下優化性能指標

(26)

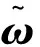
類似姿態角子系統設計方法，可以得到使性能指標(26)最小的預測控制律為：

(27)

根據定義可以計算出

定理2 對于飛行器姿態動力學子系統(8)，在形如式(27)的控制作用下，閉環系統是全局漸近穩定的。

證明 將預測控制律(27)代入飛行器姿態動力學方程(8)，可得到閉環系統方程為：

(28)

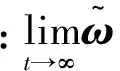
2.2.2 姿態角速度子系統的干擾觀測器設計

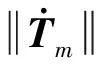
(29)

對于系統式(29)中的不確定項設計非線性干擾觀測器為：

(31)

2.2.3 姿態角速度子系統的基于干擾觀測器的廣義預測控制

設計如下帶有干擾觀測器的控制

(32)

(33)

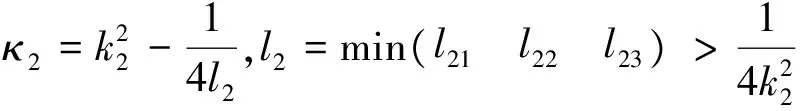
3 主要結果

定理3 對于面向姿控設計的飛行器模型式(6)和(8)，在控制律式(24)和(32)以及干擾觀測器式(22)和(30)的控制作用下，閉環系統的姿態將收斂至期望姿態附近的小鄰域之內。

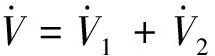
(34)

因此,閉環系統的姿態將收斂到期望姿態附近的小鄰域之內。

4 仿真分析

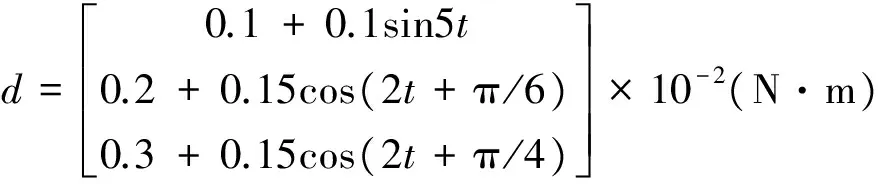
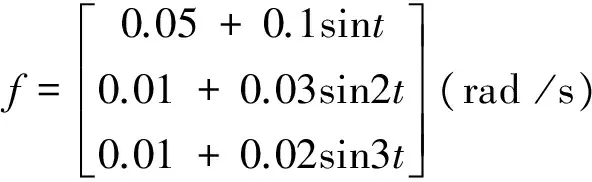
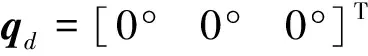
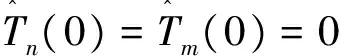
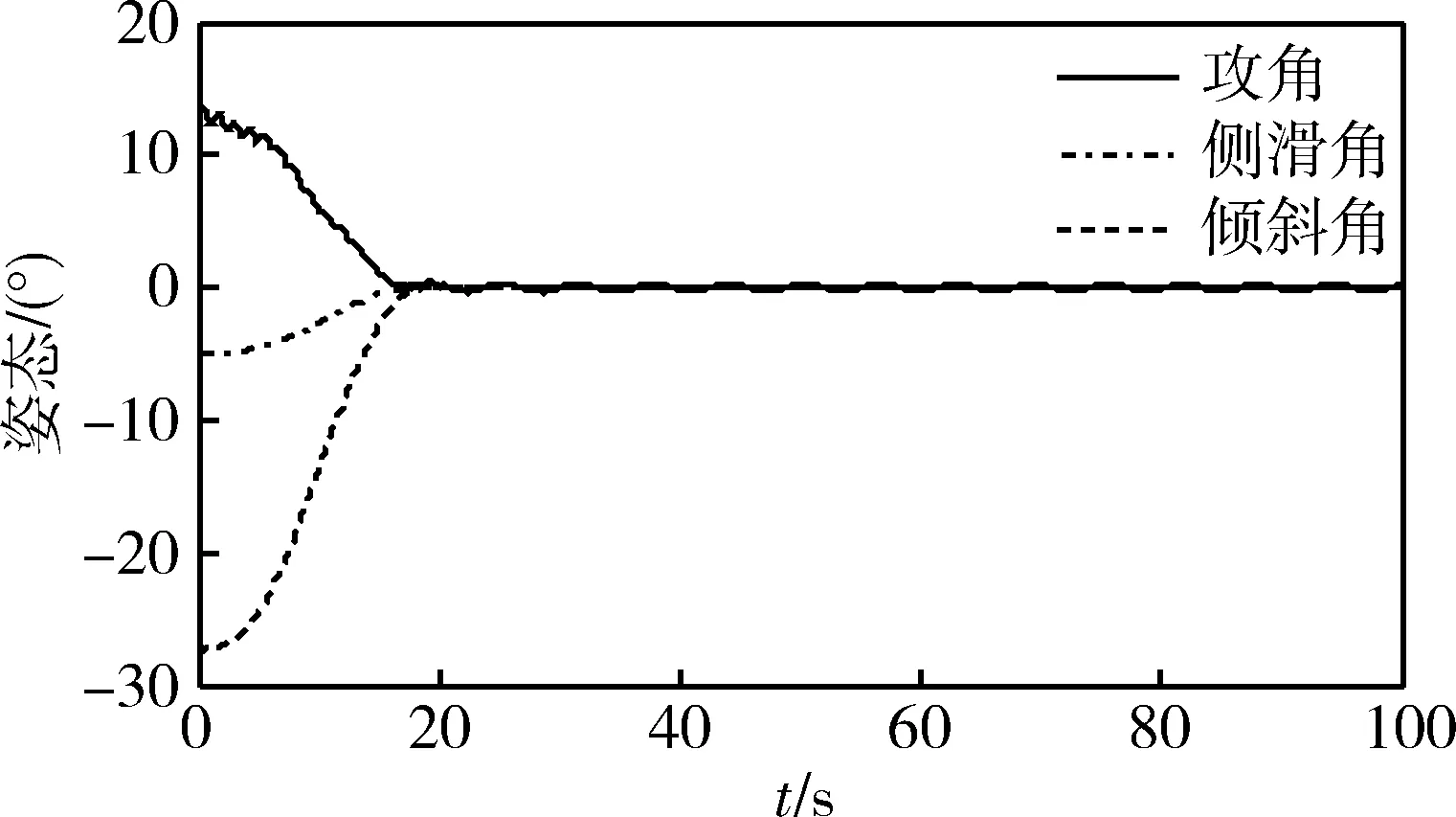
圖1 姿態角變化

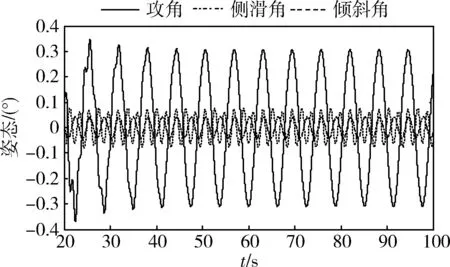
圖2 20s后的姿態變化放大

從仿真結果可以看出，盡管模型中存在較大的慣性不確定性和未知外部干擾，但利用本文所設計的控制律能使飛行器姿態收斂到期望姿態附近的有界小鄰域內，具有良好的控制精度。

5 結束語

針對再入飛行器這一不確定非線性MIMO系統，提出了一種基于非線性干擾觀測器的廣義預測控制方法。對姿態子系統，設計虛擬的預測控制，利用非線性干擾觀測器估計虛擬控制中的不確定；對于姿態角速度子系統，利用廣義預測控制方法設計真實控制輸入，同樣利用干擾觀測器對未知干擾進行逼近，為了簡化計算，在設計干擾觀測器時一并將虛擬控制的導數作為不確定進行了處理。本文充分考慮了模型中的干擾失配問題，結合廣義預測控制方法，解決了模型不確定和干擾失配對系統的影響。通過仿真驗證了所設計控制器的有效性。

[1]LuP.OptimalPredictiveControlforContinuousNonlinearSystems[J].InternationalJournalofControl, 1995, 62(3): 633-649.

[2]SoroushM，SoroushHM.Input-outputLinearisingNonlinearModelPredictiveControl[J].InternationalJournalofControl, 1997, 68(6): 1449-1473.

[3]ChenWH,BalanceDJ,GawthropPJ.OptimalControlofNonlinearSystems:aPredictiveControlApproach[J].Automatica, 2003, 39: 633-641.

[4]RecasensJJ,ChuQP，MulderJA.RobustModelPredictiveControlofaFeedbackLiberalizedSystemforaLifting-bodyRe-entryVehicle[J].AIAAGuidance,NavigationandControlConferenceandExhibit, 2005, 1-33.

[5] 秦偉偉, 劉剛, 汪立新,等. 基于參數依賴滾動時域H∞控制的高超聲速飛行器控制 [J]. 控制與決策, 2014, 29(3): 403-410. (QinWeiwei,LiuGang,WangLixin,etal.ParameterDependedRecedingHorizonH∞ControlforaHypersonicVehicle[J].ControlandDecision, 2014, 29(3): 403-410.)

[6]FanW,JiangCS.NonlinearPredictiveControlofanAerospaceVehiclebasedonAdaptiveFuzzySystems[J].ActaAeronauticaetAstronauticaSinica, 2008, 29(4):988-994.

[7]SunG,HuoW.Direct-adaptiveFuzzyPredictiveControlofSatelliteAttitude[J].ACTAAutomaticaSinica, 2010, 36(8): 1151-1159.

[8]SunG,HuoW.IndirectAdaptiveFuzzyPredictiveControlforAttitudeTrackingofSatellites[J].JournalofSystemsScienceandMathematicalSciences, 2009, 29(10): 1327-1342.

[9] 王亮, 劉向東, 盛永智. 基于高階滑模觀測器的自適應時變滑模再入姿態控制 [J]. 控制與決策, 2014, 29(2): 281-286. (WangLiang,LiuXiangdong,Sheng

Yongzhi. High-Order Sliding Mode Observer Based Adaptive Time-Varying Sliding Mode for Re-entry Attitude Control [J]. Control and Decision, 2014, 29(2): 281-286.)

[10] 王亮, 劉向東, 盛永智,等. 基于擾動觀測器的指數時變滑模再入姿態控制 [J]. 中國空間科學技術, 2013, 8(4): 31-38. (Wang Liang, Liu Xiangdong, Sheng Yongzhi, et.al. Disturbance Observer Based Exponential Time-varying Sliding Mode for Re-entry Attitude Control [J]. Chinese Space Science and Technology, 2013, 8(4): 31-38.)

[11] Chu Z Y, Cui J, Sun F C. Fuzzy Adaptive Disturbance-Observer-Based Robust Tracking Control of Electrically Driven Free-Floating Space Manipulator [J]. IEEE Systems Journal, 2014, 8(2): 343-352.

[12] Chai H Y, Yan P, Guo L. Feedback Linearization Design for Permanent Magnet Synchronous Motor with Disturbance Observer[C]. Proceedings of the 32nd Chinese Control Conference, 2013, 2739-2744.

[13] Lu H, Wang N, Qiao J Z, et al. Nonlinear Disturbance Observer Based Command Filtered Backstepping Control for Missile System[C]. Proceedings of the 32nd Chinese Control Conference, 2013, 4311-4316.

[14] 王首斌, 王新民, 謝蓉,等. 基于干擾觀測器的高超音速飛行器魯棒反步控制[J]. 控制與決策, 2013, 28(10): 1507-1512. (Wang Shoubin, Wang Xinmin, Xie Rong, et al. Robust Backstepping Control Based on Disturbance Observer for Hypersonic Vehicle [J]. Control and Decision, 2013, 28(10): 1507-1512.)

[15] Jin S, Zhang Z X, Li S H. Design of Guidance Law Based on Nonsingular Terminal Sliding Mode Control and Finite-Time Disturbance Observer [J]. 13th IEEE Workshop on Variable Structure Systems, 2014.

[16] Desai P N, Conway B A. Six-Degree-of-Freedom Trajectory Optimization using a Two-Timescale Collocation Architecture [J]. Journal of Guidance, Control, and Dynamics, 2008, 31(5): 1308-1315.

Generalized Predictive Control of Vehicle Re-entry Attitude Based on Disturbance Observer

Sun Guang, Zhu Ruyi, Wang Zheng

Research and Development Center, China Academy of Launch Vehicle Technology, Beijing 100076, China

Ageneralizedpredictivecontrolmethodbasedonnonlineardisturbanceobserverisproposedforre-entryvehicleinreentryphaseduetothemodeluncertaintyandmismatchdisturbances.Firstly,thevirtualpredictivecontrolisinvolvedinattitudesubsystemandtheunknowndisturbancesofcontrollerisestimatedbyusingnonlinearobserver.Secondly,theactualcontrolinputisdesignedbyusingthemethodofgeneralizedpredictivecontrolwithattitudeangularvelocitysubsystem.Inordertosimplifycalculation,thederivateofvirtualcontrolandunknowndisturbancesintheactualcontrolareestimatedbyusingnonlinearobserver.Finally,theattitudetrackingerrorisconvergedtoaboundedneighborhoodofdesiredattitude,whichisbasedontheLyapunovanalysis.Thesimulationresultsshowtheeffectivenessofthemethod.

Re-entryvehicle;Disturbanceobserver;Generalizedpredictivecontrol

2015-10-14

孫 光(1980-)，男，山東人，博士研究生，工程師，主要研究方向為飛行器導航、制導與控制；朱如意(1985-)，女，安徽人，碩士研究生，工程師，主要研究方向為飛行器導航、制導與控制；王 征(1986-)，男，北京人，碩士研究生，工程師，主要研究方向為飛行器導航、制導與控制。

TP273

A

1006-3242(2016)04-0010-06