淺談求函數值域的幾種常用方法
王奕先
(濟南市歷城第二中學 山東濟南 250104)
?
淺談求函數值域的幾種常用方法
王奕先
(濟南市歷城第二中學 山東濟南 250104)
摘 要:函數的值域是函數的重要性質之一,也是學習中的難點之一。求函數的值域,在知識上,除涉及函數的所有知識外,還需要二次函數、不等式等其他重要知識點;在解題方法上,具有較強的綜合性,求函數值域是一個比較復雜的問題,不同的函數解析式要用不同的方法,選擇正確簡潔的求值方法對于求函數值域的相關知識會有很大的鞏固和提高。可以把求函數的值域歸納為下列幾種類型
關鍵詞:函數值域 解答 方式方法
求函數值域是一個比較復雜的問題,不同的函數解析式要用不同的方法,下面舉例說明幾種常見的求函數值域的方法。[1]
一、配方法
例1求函數y=2x2-6x+3的值域
二、判別式法
對于某些有理數分式函數,y=f(x)(分子或分母最高次數為2),可把函數的解析式化為關于x的一元二次方程,再根據判別式△≥0得到一個關于y的不等式。解此不等式就可求得函數的值域。
當y=1時,x=0屬于定義域
三、非負數法
當函數的解析式中出現絕對值,偶次方冪,算數根和指數冪時,常根據他們的非負數這一性質確定函數的值域。[2]
四、分部分式法
當函數的解析式y=f(x)是分式且分子的次數大于或等于分母的次數時,可分部分式求函數的值域。[3]
故該函數的值域為[y∶y∈R且y≠1]
五、換元法
對于某些特殊的函數y=f(x),可利用設輔助未知數的方法求得其值域。
里奇是基于傳統攝影底片照片的保存中可能存在的損傷老舊,從而暗示人們亙古以來的藝術品膜拜和商品拜物教觀念將在數碼時代的攝影中被蕩平。因為數碼攝影是以馬賽克形式存在,副本與原作沒有區別,追求“原作”行為在數碼攝影中毫無意義,從而為論證數碼攝影的優勢、社會性使用以及與賽博格的聯姻打下基礎。認識到這一點尤為重要,正是人們對攝影的復制性、靈活性和融合性等的科學認識和技術開發,攝影才能夠與任何媒介交互關聯,成為“融媒介”和“超攝影”,發揮政治的、商業的、社會的、科學的和文化的功用,而不僅僅囿于藝術的窠臼。
六、函數的單調性法
對于某些單調函數可根據函數的單調性求函數的值域。
七、反函數法
因為原函數的值域正好是它的定義域,所以要求原函數的域可以轉換為先求其反函數再求其定義域,即得原函數的。[4]
八、數形結合法
將此函數化為分段函數的形式
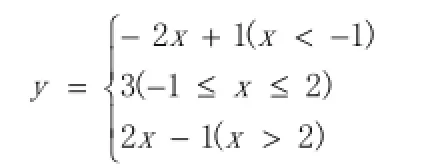
以后通過學習不等式和三角函數求函數的值域還可以用不和利用有界性法。
參考文獻:
[1]陳惠.三角函數的值域(最值)的類型及常用求法
[2]如何求函數值域[J];云南教育(基礎教育版);1980年09期
[3]黃桂香.求函數值域的常用方法《中學課程輔導·教學研究》2012年第30期
[4]周云.求函數值域的方法歸納《考試周刊》2009年18期

