海量隨機數碰撞率檢測的快捷方法

孟秀哲　楊棟毅

摘 要： 針對海量隨機數碰撞率實時檢測的需求，利用隨機數的隨機特性，結合文件系統路徑編碼的方式，提出了一種類似于平衡B叉樹的平衡檢索森林的結構與算法。該方法避免了平衡B叉樹的編程復雜性，檢測效率非常高，有效地解決了海量隨機數碰撞率檢測因耗時量過大而難以在工程上快速實現的問題。

關鍵詞： 隨機數； 海量隨機數； 碰撞率檢測； 路徑編碼； 平衡檢索森林

中圖分類號：TP391 文獻標志碼：A 文章編號：1006-8228（2016）08-44-03

Abstract： For the demand of real-time detection of massive random number collision rate， by using the stochastic properties of the random number and the file system path coding， a method of balanced search forest similar to the balanced B search tree is proposed. This method avoids the programming complexity of the balanced B search tree， and the detection efficiency is very high. It can effectively solve the problem that the collision rate detection of massive random number is too much time consuming to be quickly realized in engineering.

Key words： random number； massive random number； collision rate detection； path coding； balanced search forest

0 引言

隨機數對于系統仿真[1]、信息通訊[2]、計算機隨機模擬[3]、隨機局部搜索[4]、密碼研究[5]、隨機驗證碼、彩票博弈、實驗設計和隨機抽樣等領域或方面都有著十分重要的作用。隨機序列的隨機性，主要體現在兩個方面，一是這個序列的產生是無法確定的，而且是不可以復現的；二是這個序列具有統計特性，當序列足夠長時，其中的0和1的個數趨于相等，即具有0、1的均勻性。前者可以用碰撞率來測度，后者可以用均勻性來測度。碰撞率就是讀取或產生一系列的32位隨機數，統計隨機雙字的重復次數，最理想的結果就是碰撞次數為0。

海量隨機數的數據量非常大，常常是邊產生邊檢驗，這就需要維持一張表，不斷登記檢測過的隨機數，統計鍵值重復的次數。隨著檢測過程的不斷加長，這張記錄表會越來越大。如果采用順序查找，則編程簡單，但效率低下，平均查找次數約為（N+1）/2[6]，N為表中記錄數。如果采用二分查找，則需要對順序表進行排序，開銷可能超過二分查找所節省的時間。“使用二叉樹結構，不僅能有效地查表，而且還能迅速地插入和刪除記錄”[7]，二叉樹結構因為復雜而使得編程變得困難。為此，我們提出了用于海量隨機數碰撞率實時檢測的平衡檢索森林的巧妙思想與簡捷方法。

1 平衡檢索森林的基本原理

1.1 基本思想

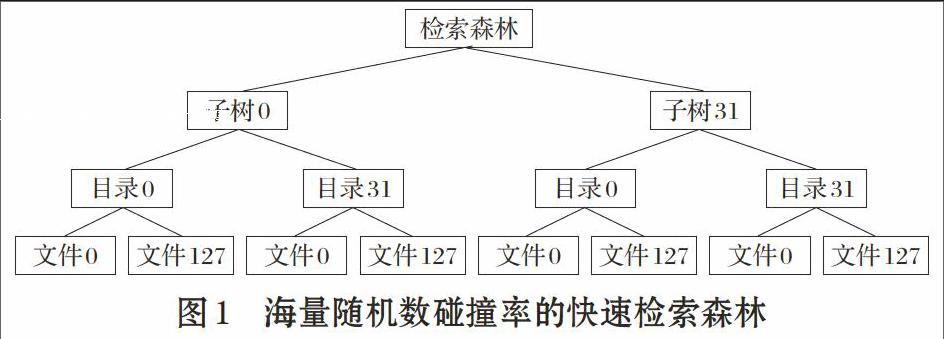
在平衡檢索森林中，葉子文件的訪問是通過隨機數位段編碼的方式均勻地進行，葉子文件訪問的均勻性源于隨機數位段的隨機性。快速檢索森林是靜態平衡的，而不需要像平衡B叉樹那樣，需要動態維護節點的平衡[8]，這是快速檢索森林的一大特性與優勢，即沒有額外的維護開銷。通過對每個隨機數四個位段的編碼（詳見2、平衡檢索森林的編碼規則），分別形成子樹、目錄和文件的地址，以及，記錄的鍵值。路徑與鍵值兩方個面的編碼使得葉子文件均勻分布在整個檢索森林之下，巨大單一文件被分割為巨量小文件。

假定隨機數具有30比特有效信息，則不重復隨機數文件最多有230=1073741824條記錄，接近海量數據。我們不是在一個巨型文件中存儲或檢索這10億多條記錄，而是將這棵巨大無比的單枝樹，人為地切分成一片均勻森林，由32棵樹組成，每棵樹有32個樹杈，每個樹杈下面有128片葉子，葉子即子文件，每個葉子最多只有8192條記錄。葉子文件共有：32*32*128=25*25*27=217=131072（個）。對于一個30比特的隨機數進行檢索的過程，實際上就是根據鍵值的四個位段來定位某棵樹、某樹杈、某文件及某條記錄的過程。其中，對樹、樹杈及文件的定位，是不需要耗費時間的，它體現在文件路徑的編碼上面；對記錄的查找采用簡單的順序檢索方式進行，隨機數記錄的維護也采用尾部添加的簡單方式順序存儲。檢索過程中，若子鍵值不存在，則將其添加于某個子文件尾部；若子鍵值存在，則碰撞次數++，子鍵值不添加于子文件尾部。

1.2 編碼規則

⑴ 對于任意一個30位的隨機數，按照四個位段編碼如下：

該森林32棵樹的編號（0到31）由隨機數的高5位（位29到25）決定，000002 到111112分別對應子樹0到子樹31。某棵樹32樹杈的編號（0到31）由隨機數的次5位（位24到20）決定。某樹杈128個葉子文件的編號（0到127）由隨機數的次次7位（位19到13）決定。而隨機數的最后13位（位12到0）作為30位隨機數的代表儲存于小文件中，子文件的記錄數最多為213=8192條，這樣，一個巨型文件的海量檢索就被化簡為一個小文件的小規模順序檢索。

⑵ 假定當前隨機數的十進制數值為123456789，則十六進制數為0x75BCD15，二進制數為1110101101111001101000101012，不足30位前補0，為（00011）（10101）（1011110）（0110100010101）2，下標2表示二進制。

⑶ 該隨機數對應樹的編號由鍵值的高5位（即第一個括號里面的5比特）決定，上述鍵值所在樹的編號即為000112=3。

⑷ 該隨機數對應樹杈的編號，由鍵值的次5位（即第二個括號里面的5比特）決定，上述鍵值所在樹杈的編號即為101012=21。

⑸ 該隨機數對應樹葉（即子文件）的編號，由鍵值的次次7位（即第三個括號里面的7比特）決定，上述鍵值所在樹葉的編號即為10111102=94。

⑹ 上述鍵值的末13位（即第四個括號里面的13比特），用來表示一個子文件的鍵值記錄，順序存儲或檢索不超過8192條的13位子鍵值，比順序存儲或查找1073741824條主鍵值要快得多。當前子文件的子鍵值為01101000101012=3349。

由鍵值的四個位段，可以定位隨機數位于：子樹3、樹杈21、樹葉94、子鍵值3349，用符號表示即為：tree[3]、Branch[21]、leaf[94]、subkey[3349]。

2 平衡檢索森林的算法實現

2.1 數據結構

為了便于編程實現，需要將上述形象的檢索森林，轉化為抽象的二級文件目錄結構。

⑴ 檢索森林對應的根目錄定義為：“D：＼＼SF”。

⑵ 樹0到樹31對應的一級子目錄定義為：“D：＼＼SF＼＼T0”到“D：＼＼SF＼＼T31”。

⑶ 樹i的樹杈0到樹杈31對應的二級子目錄定義為：“D：＼＼SF＼＼Ti＼＼B0”到“D：＼＼SF＼＼Ti＼＼B31”，i=0 to 31。

⑷ 樹i的樹杈j下的128個文件名定義為：“D：＼＼SF＼＼Ti＼＼Bj＼＼L0.bin”到“D：＼＼SF＼＼Ti＼＼Bj＼＼L127.bin”，i=0 to 31，j=0 to 31。

⑸ 整個檢索森林就有32*32*128=131072個子文件，為了查找子鍵值的簡單，文件采用二進制格式，這里，“.bin”的文件擴展名特指二進制格式。

⑹ 如此龐大數量的子文件，不論是建立，還是刪除，都需要花費一定的時間，但是，換來的好處就是每個文件都很小，檢索起來非常快。

2.2 算法描述

Step1 初始化檢索森林，只生成兩級子目錄。

Step2 生成32*32*128個二進制空文件，若原來文件中有子鍵值記錄，則自動清空。

Step3 產生或讀取30位的隨機數。

Step4 依次讀取該隨機數的前三個位段，根據平衡檢索森林的編碼規則（見表1）拼接構造出葉子文件的路徑名。

Step5 打開該樹葉文件。

Step6 取該隨機數的最后13位，形成葉子文件的鍵值，順序比較該文件中的全部記錄，若鍵值存在，則碰撞次數++；若不存在，則將該鍵值添加到該葉子文件尾部。

Step7 關閉葉子文件。

Step8 終止循環嗎？if（終止） then {goto Step 10}。

Step9 goto Step 3。

Step10 碰撞率=碰撞次數/隨機數的總數。

Step11 結束。

3 效率分析與實驗結果

3.1 效率分析

假定30位隨機數的記錄數量為N，且每一個葉子文件的碰撞率檢測采用簡單的二進制文件順序檢索方法，則每個葉子文件的記錄數平均為：M=N/（32*32*128）=N/217。對于順序文件查找，如果每個輸入鍵碼都以相同的概率出現，則在一次成功的查找中，鍵碼與順序表中記錄的比較次數：

C=（1+2+3+4+…+M）/M[9]=（M（M+1）/2）/M

=（M+1）/2=（N/217+1）/2=（N/218+0.5）≈N/218

標準差約為0.289M[10]=0.289*N/217，因此，平衡檢索森林中隨機數的平均檢索效率約為N/218。

3.2 實驗結果

實驗條件為個人臺式機，操作系統為Microsoft Windows XP SP3，CPU為Genuine Intel（R） 1.60GHZ，2GB內存。對于平衡檢索森林中龐大數量的子文件，首次建立過程需要4分鐘，非首次建立過程需要3分10秒，刪除過程需要3分50秒。對于2560Kbyte的二進制隨機數文件，需要3小時45分檢測完畢。2560Kbyte的二進制隨機數的檢測結果如下：記錄數=655360，碰撞數=47，碰撞率=0.000072，合格閾值=0.0001，本次碰撞率測試合格。

4 結束語

在海量隨機數碰撞率的實時檢測項目中，我們提出了平衡檢索森林的結構與方法，不僅為開發與測試帶來了高度的簡便性與可靠性，而且，為海量隨機數碰撞率的檢測帶來了極高的效率。但這種結構與方法也存在著一定的問題，就是當隨機數的隨機性能不是很好的時候，這個檢索森林的平衡性會受到一定程度的影響。下一步的研究重點是將葉子文件記錄查找方法與雜湊（HASH）技術相結合，進一步提高檢索森林在隨機數的隨機性不是很好狀況下的檢索效率。

參考文獻（References）：

[1] 楊睿.論偽隨機序列及其應用[J].沈陽工程學院學報（自然科學版），2009.5（2）：168

[2] 江裕劍等.計算機模擬隨機數發生器的產生、檢驗及應用[J].成都電訊工程學院學報，1983.1：117

[3] 張廣強.均勻隨機數發生器的研究和統計檢驗[D].大連理工大學碩士學位論文，2005.

[4] 欒忠蘭等.偽隨機數發生器的統計性質檢驗及其應用[J].計算機應用與軟件，2010.27（10）：168

[5] 盧開澄.計算機密碼學（第2版）[M].清華大學出版社，1998.

[6] （美）Donald E. Knuth著，蘇運霖譯.計算機程序設計藝術 第3卷排序與查找（第2版）[M].國防工業出版社，2003.

[7] （美）Donald E. Knuth著，蘇運霖譯.計算機程序設計藝術 第3卷排序與查找第2版[M].國防工業出版社，2003.

[8] （美）Donald E. Knuth著，蘇運霖譯.計算機程序設計藝術 第3卷排序與查找（第2版）[M].國防工業出版社，2003.

[9] （美）Donald E. Knuth著，蘇運霖譯.計算機程序設計藝術 第3卷排序與查找（第2版）[M].國防工業出版社，2003.

[10] （美）Donald E. Knuth著，蘇運霖譯.計算機程序設計藝術 第3卷排序與查找（第2版）[M].國防工業出版社，2003.