對隨機性復合標底法投標報價策略的研究

黃朝煊,方詠來,袁文喜,李水瀧,趙　勇

(浙江省水利水電勘測設計院,浙江 杭州　310002)

?

對隨機性復合標底法投標報價策略的研究

黃朝煊,方詠來,袁文喜,李水瀧,趙勇

(浙江省水利水電勘測設計院,浙江 杭州310002)

摘要：基于博弈論中的混合戰略納什均衡,采用概率理論和數值分析理論研究隨機性復合標底法中最優投標報價,利用二次多項式等效非線性函數,給出連續型隨機性復合標底法下最優報價的解析計算式,對于離散型隨機性復合標底法可采用連續型等效,也可采用枚舉法結合Matlab編程求解,通過工程實際競標案例,驗證該理論具有極好的工程實際應用價值。

關鍵詞：隨機性復合標底法;混合戰略納什均衡;投標報價策略;最優報價;解析計算式

招投標包含招標和投標2種形式,招標和投標是商品交易方式[1],是市場經濟中交易過程的2個方面,也是國際慣例。招標投標活動中的主要參與人是招標人和投標人。

工程投標報價理論由Emblem[2]提出， 隨后Friedman[3]發表了投標報價的研究成果，眾多學者在Friedman基礎上提出了多種模型，如：Gate模型[4]、Carr R I模型[5]等，其研究方法均采用決策和對策論，但模型的假設約束條件很強，在工程實踐應用中存在較大缺陷。

胡軍峰等[6]將博弈論應用于電力需求價格的均衡分析中;盧德林等[7]對土建工程報價優化模型進行了研究,但對隨機性因素的考慮均不足；阮連法等[8]將博弈論理論應用到建筑工程投標報價中,但模型過于簡單,不便于實際投標報價應用;胡靜[9]對多家企業投標報價狀況進行調查分析,并對復合標底法建立了簡易投標報價模型,但該模型對投標參與者的相關歷史信息要求有充分了解,與工程實際不符。歐陽益[10]也對復合標底法進行了初步研究,認為所有投標人報價均理性地朝最接近復合標底的最高分值貼近。

以上學者的研究均未涉及常用的隨機性復合標底法,因此,筆者基于博弈論中混合戰略理論,對隨機性復合標底法投標報價策略進行了研究。

1　隨機性復合標底法

隨機性復合標底法在復合標底中增加了隨機性,使得招投標更公平公正,其中隨機性復合標底法中復合標底計算公式

(1)

(2)

式中:C為評標中的復合標底;A為業主的期望標底,一般在開標現場以隨機搖號法確定,取值范圍為A∈(a1,a2),記其概率密度函數為:f(A);β為業主在開標現場以隨機搖號法確定的權重系數,取值范圍為β∈(β1,β2), 記其概率密度函數為:g(β);Bi為第i家投標單位的報價,取值范圍在業主規定的報價范圍內,即Bi∈(Bmin,Bmax);n為投標單位的總個數;μ為最優報價下浮率,暫取μ=0。

2　混合戰略理論在隨機性復合標底法中的應用

2.1 隨機性復合標底投標報價博弈模型

隨機性復合標底投標報價博弈模型的建模要求是根據投標人競爭信息情報、戰略、報價效用等,利用博弈規則預測報價均衡,確定最優的報價,其基本框架為:

a. 參與人:有n個投標人參加投標。

b. 信息:對業主及投標競爭對手的信息完全互相不了解。

c. 戰略:報價是每個投標人自己的戰略,所有投標人的報價均在業主規定范圍Bmin≤Bi≤Bmax。

d. 博弈規則:評標中評分標準為隨機性復合標底法,復合標底由業主設定的隨機標底與所有投標人有效報價按照隨機權重系數復合確定(式(1)),最優報價為復合標底按下浮率μ計算確定報價(本文暫取μ=0),投標人報價等于最優報價得滿分;投標人報價高于最優報價每1%扣1分;低于最優報價每1%扣0.5分(實際招標中扣分值可能會不盡相同,但一般高報價的扣分值會大于低報價)。

e. 效用:工程實際競標中一般具有唯一性,即只有唯一中標人。

f. 投標人報價目的:在報價不低于當前市場成本的情況下獲得最高報價得分,即報價最接近于最優報價,則投標人i報價Bi的支付為

(3)

式中：ui為投標人i報價Bi時的支付函數(得分);h為投標報價滿分。

以上即為隨機性復合標底的投標報價博弈模型。投標人i的關鍵任務是對最優報價D進行預測,使得自己的報價得分最高,這個最優報價對所有投標人是均等的,即存在穩定的納什均衡。

2.2隨機性復合標底投標報價博弈模型的納什均衡解的存在性

納什均衡，即非合作博弈均衡。納什均衡分成兩類：純戰略納什均衡和混合戰略納什均衡，筆者研究的隨機性復合標底投標報價博弈模型屬于混合戰略納什均衡。

根據納什均衡的3條存在性定理[11]，以及工程實際中投標競標的特征，奠定了建筑及水利工程投標報價的博弈均衡解存在性的理論基礎。

2.3 隨機性復合標底投標報價博弈模型的混合戰略納什均衡解的求解

對于連續型變量,當業主期望的隨機標底在A∈(a1,a2)范圍內按一定概率分布隨機變動、隨機權重系數在β∈(β1,β2)范圍內按均布概率隨機變動時,即所有投標人均朝著最優報價目標報價,第i個投標人報價Bi的計算報價評分期望值為

(4)

(5)

式中:H為投標人i報價等于最優報價D時的支付值;F(Ai)為業主期望標底Ai相應的概率密度分布函數;g(βi)為權重系數β連續概率密度函數。

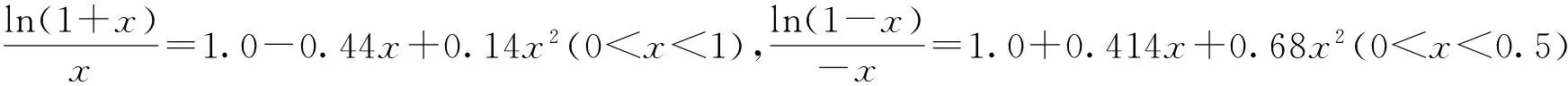
(6)

D3+b2D2+b1D+b0=0

(7)

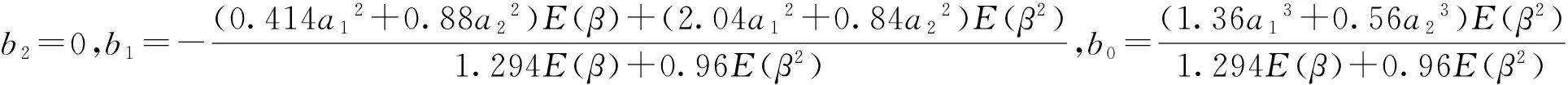
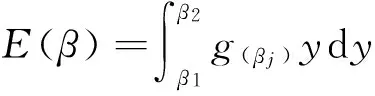
(8)

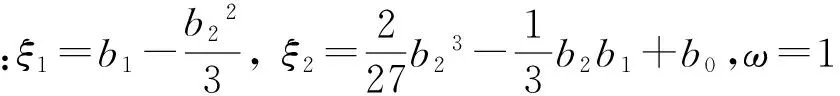
對于離散型隨機變量,可通過Matlab軟件列舉法求解,也可以采用連續型等效,關鍵是采用連續型概率分布等效離散概率分布,其最優報價D值解基本一致的。

3　案例分析

3.1案例

沿海地區某圍涂項目總圍墾面積約2 800 hm2,海堤總長23.6 km、排澇水閘7座、交通隔堤及配套工程等。

a. 發包范圍:初步設計、招標設計、施工圖設計。內容包括初步設計報告、招標圖紙及技術條款和工程量清單、施工圖等。

b. 質量要求:符合國家規定及技術規范要求。

c. 招標人的工程總設計費測算價(最高限價)為1 283萬元。其中投標報價評分細則為:①最佳報價值=業主期望標底×(調整系數)%+符合條件的報價平均值×(100-調整系數)%;②符合條件的報價區間以招標人測算價1 283萬元(含)為上限,以測算價下浮8%為下限(取整數1 180萬元,含本數)；③業主期望標底為1 150萬～1 250萬元(1 150、1 160、1 170、1 180、1 190、1 200、1 210、1 220、1 230、1 240、1 250)中隨機抽取的1個數；④調整系數從0～4(0、0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0)中隨機抽取的3個數的平均值,保留二位小數；⑤報價得分評判原則為報價等于最佳報價值的得滿分60分，報價每低于最佳報價值1個百分點扣0.5分，報價每高于最佳報價值1個百分點扣1分，報價得分不足一個百分點時,使用直線插入法計算,保留二位小數。報價最低得分為56分。其中,低于報價區間下限的投標報價為有效報價,但不作為計算報價平均值的基礎。當所有報價均低于報價區間下限時,則以報價區間下限1 180萬元為報價平均值。

3.2模型建立與求解

根據招標文件可知,業主期望標底A在1 150萬～1 250萬元之間滿足均布概率分布,調整系數β為0 ～ 4(0、0.5、1.0、1.5、2.0、2.5、3.0、3.5、4.0)中隨機抽取的3個數的平均值,根據排列組合理論可知,調整系數β的概率分布如圖1所示。

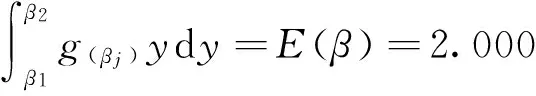
若采用連續函數等效離散的調整系數β的等效連續型概率密度函數為

Pβ=5.963×β(4-β)(3.65×10-3β4-2.92×10-2β3+

0.071β2-0.051β+0.0172)

根據本文解析計算理論可知,投標人最優報價為D=1 213萬元,見圖2。

最終開標結果為:①業主的期望標底通過搖號確定為A=1 190萬元；②β通過搖號獲得3個數(2.5、1.0、1.5),即確定β=(2.5+1.0+1.5)/3=1.667。③根據招標文件確定最終的最優報價為:1 205.73萬元。

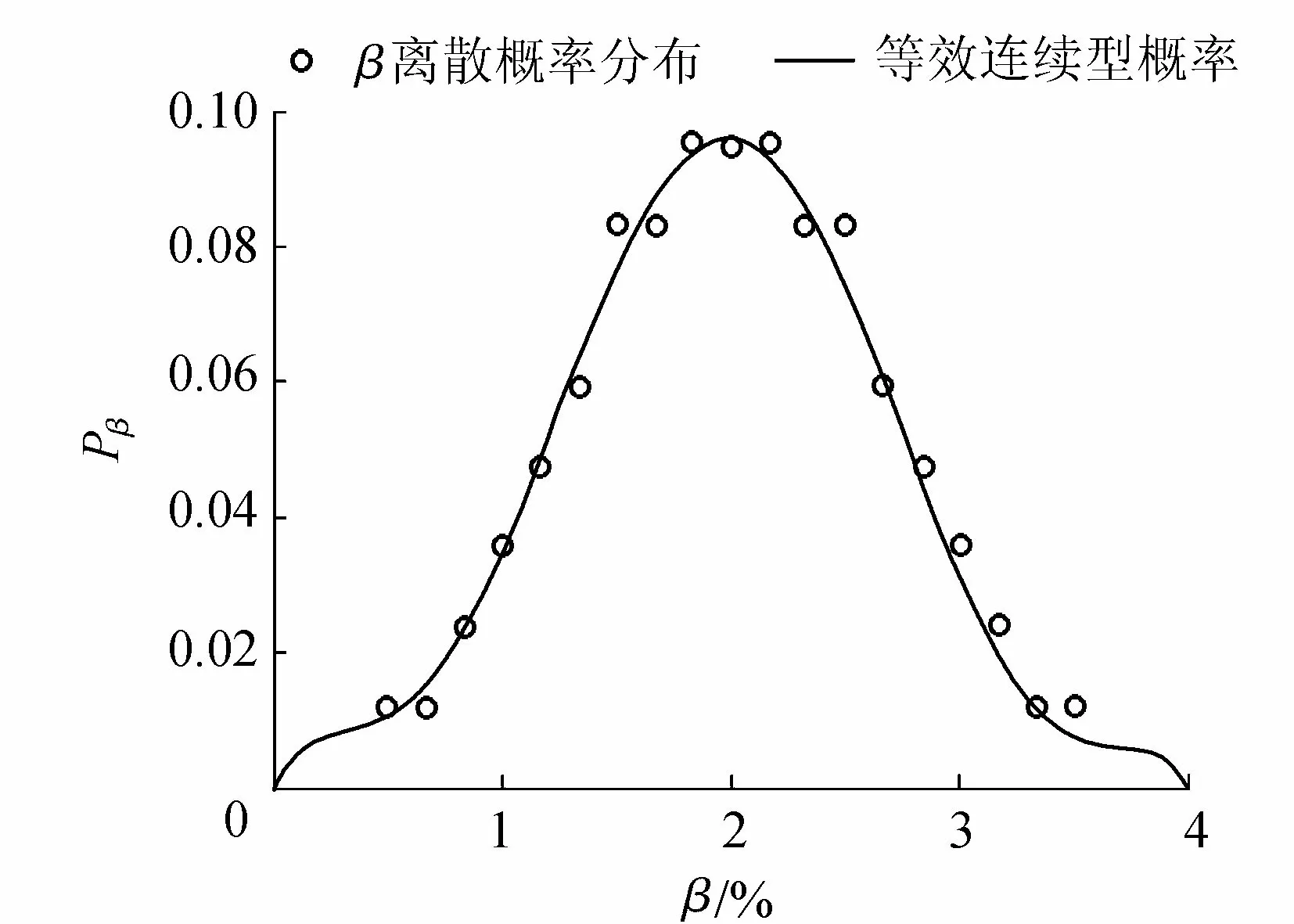
圖1　調整系數β的概率分布

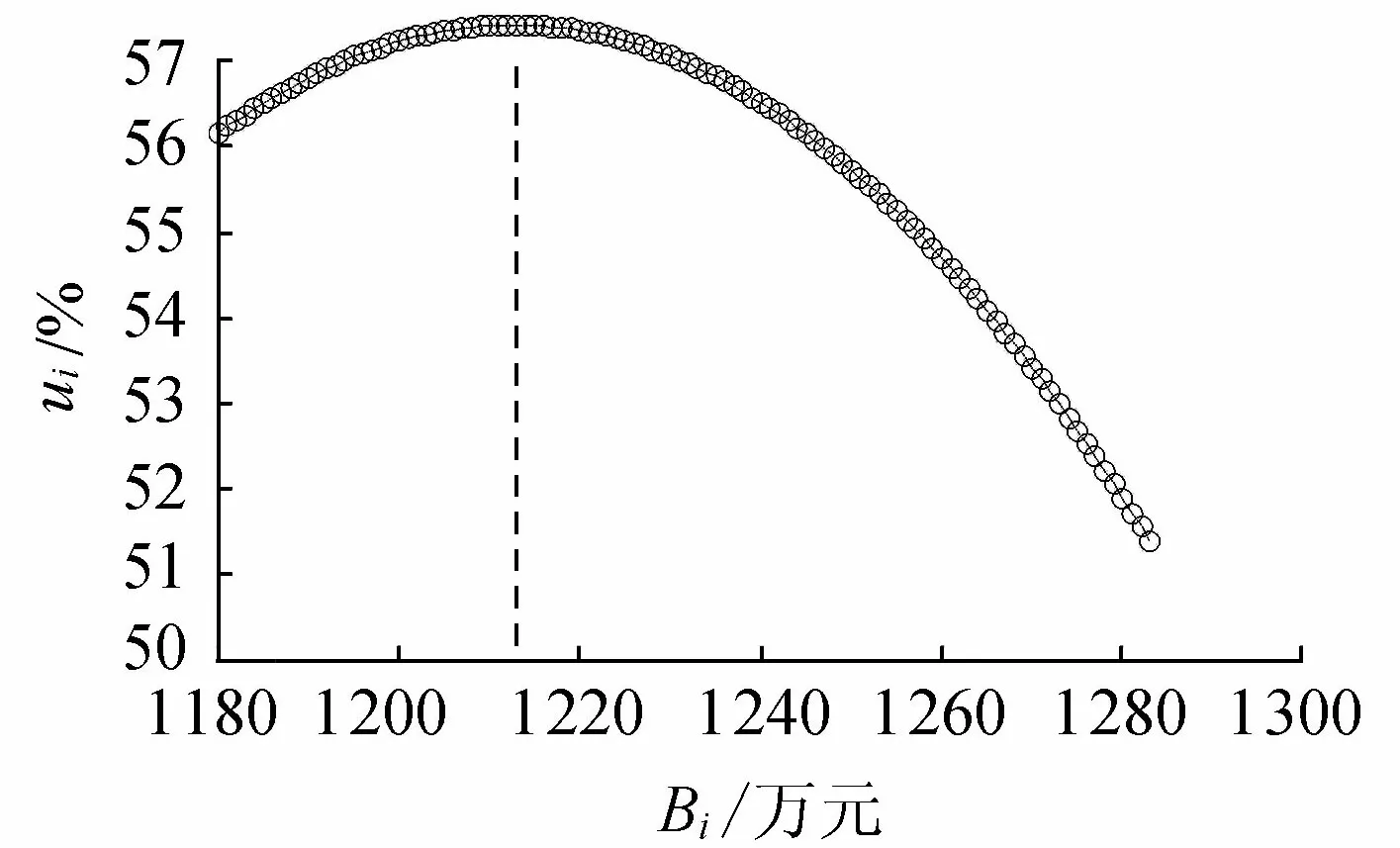
圖2　投標人不同報價下的支付函數關系曲線

依據招標文件評分細則,計算各投標人得分(表1)，最終投標人甲以1210萬元報價獲得最高分,并中標,說明該理論具有較好的工程應用價值。

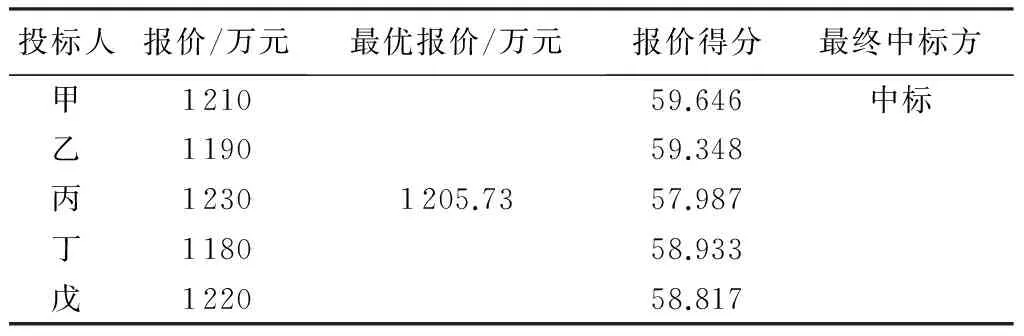
表1　最終開標結果統計

4　結　語

隨機性復合標底法以其特有的公平公正性,在工程實際招標中被普遍采用,筆者基于博弈論中的混合戰略納什均衡為理論基礎依據,對隨機性復合標底法中最優投標報價進行了研究,主要結論如下:

a. 依據博弈論和概率理論建立了隨機性復合標底法投標報價模型,依據最大支付值原理給出了連續型、離散型隨機性復合標底法的最優報價計算方程。

b. 利用數值分析理論及二次多項式等效非線性函數,根據數值極值理論給出了最優報價的一元三次方程,并采用卡當公式直接給出了連續型隨機性復合標底法下最優報價的解析計算式。對于離散型隨機性復合標底法可采用連續型等效,也可采用枚舉法結合Matlab編程求解。

c. 最后通過某工程實際競標案例,驗證了該理論具有極好的工程實際應用價值。

參考文獻：

[ 1 ] 寧素瑩.建設工程招標投標與管理[M].北京:中國建材工業出版社,2003.

[ 2 ] EMBLEM D.Competitive bidding for corporate securities[D].New York: Dissertation,Colubia University,1944.

[ 3 ] FRIEDMAN L.A competitive bidding stratege [J].Operation Research,1956,4,104-112.

[ 4 ] GARES M.A didding strategy based on ESPE [J].Cost Engineer,1983,25,27-35.

[ 5 ] CARR R I.Competitive bidding and opportunity costs[J].Journal of Construction Engineering and Management ASCE,1987，113(6)：151-165.

[ 6 ] 胡軍峰,李春杰,趙會茹,等.基于博弈論的電力需求價格彈性與發電市場均衡關系[J].中國電機工程學報,28(1):89-94.

[ 7 ] 盧德林,章祥蓀,馬桂芝.土建工程報價優化模型[J].系統工程理論與實踐,2002,22(9):47-53.

[ 8 ] 阮連法,匡亞萍,吳顯.博弈論在建筑工程投標報價中的應用[J].建筑經濟,2002(6):26-28.

[ 9 ] 胡靜.基于博弈論的施工企業投標報價行為研究[D].杭州:浙江大學,2004.

[10] 歐陽益.工程項目投標報價的研究[D].蘇州:蘇州大學,2006.

[11] 謝識予.經濟博弈論 [M].上海:復旦大學出版社,2006.

基金項目：水利部公益性行業科研專項(201401010)

作者簡介：黃朝煊(1983—),男,湖北黃石人,工程師，碩士,主要從事水工結構及巖土工程研究。E-mail: 516227811@qq.com

DOI：10.3880/j.issn.1003-9511.2016.04.004

中圖分類號：F284

文獻標識碼：A

文章編號：1003-9511(2016)04-0013-04

(收稿日期：2015-12-03編輯：方宇彤)