Buck變換器的電壓電流雙閉環終端滑模控制

王艷敏,　曹雨晴,　夏紅偉

(1.哈爾濱工業大學 電氣工程及自動化學院, 黑龍江 哈爾濱 150001；2.哈爾濱工業大學 航天學院, 黑龍江 哈爾濱 150001)

?

Buck變換器的電壓電流雙閉環終端滑模控制

王艷敏1,曹雨晴2,夏紅偉2

(1.哈爾濱工業大學 電氣工程及自動化學院, 黑龍江 哈爾濱 150001；2.哈爾濱工業大學 航天學院, 黑龍江 哈爾濱 150001)

針對傳統單閉環線性滑模控制Buck變換器中存在的響應速度慢、穩態精確度低等問題，提出一種電容電壓/電感電流雙閉環終端滑模控制方法。考慮負載電阻未知情況，設計負載估計器，限制負載電流在額定范圍內以實現過流保護；基于基爾霍夫定律建立Buck變換器在開關導通和關斷兩種情況下的統一微分方程模型。針對外環電容電壓環和內環電感電流環，分別設計終端滑模控制器和線性滑模控制器以滿足其不同的控制性能要求，實現電容和電感非線性器件的瞬態性能控制，并在有限時間內輸出期望的直流電壓。基于滑模存在條件，推導出保證Buck變換器在開關導通和關斷兩種情況下的統一穩定條件。與傳統單閉環線性滑模控制方法的仿真對比證明所提控制方法的有效性和可行性。

滑模控制；終端滑模控制；Buck變換器；雙閉環控制；有限收斂

0　引　言

直流變換器(DC-DC Converter)作為一種將固定直流電壓降壓為可變直流電壓的電力電子設備，屬于一類包含開關特性的變結構系統。大量的研究證明滑模控制(sliding mode control,SMC)已成為直流變換器一種有效而應用前景廣闊的魯棒控制方法[1]，其繼電控制特性與直流變換器具有強適應性；卓越的魯棒性和瞬態響應特性可滿足其不同電路拓撲、不同場合、不同電子設備的大工作范圍電壓輸出品質要求。

以Buck拓撲型變換器為例，目前滑模控制方法在直流變換器中的應用仍以傳統的單閉環線性滑模為主，即通常僅選取電感電流[2]或電容電壓[3-4](多數情況下等于輸出電壓)之一作為控制變量來構造線性滑模面。然而，線性滑模具有的漸近收斂特性決定著系統狀態以指數形式漸近趨近卻永遠無法到達平衡點，這必然會帶來系統響應速度慢、穩態誤差大等突出問題[5]。同時，Buck變換器是一類典型的時變非線性系統，包含的電容和電感等儲能元件的非線性直接影響著系統的瞬態響應和輸出電壓品質；然而目前Buck變換器的控制器設計多基于Middlebrook等[6]提出的狀態空間平均模型，其模型的線性化僅能保證系統的局部穩定性，且往往僅考慮開關導通或關斷一種情況。因此有必要同時對電感電流和電容電壓進行實時控制。

本文基于基爾霍夫電壓和電流定律建立Buck變換器在開關導通和關斷兩種情況下的統一微分方程模型，在負載電阻未知情況下提出一種電容電壓/電感電流雙閉環終端滑模控制方法，實時控制電容電壓和電感電流的非線性瞬態變化，利用終端滑模的有限時間收斂性來改善Buck變換器輸出電壓品質。與傳統單閉環線性滑模控制方法的仿真對比證明所提方法的有效性和可行性。

1　Buck變換器的統一微分方程模型

Buck變換器的電路拓撲如圖1所示，其中E為輸入的直流電壓源，V為可控開關管，其工作狀態用u表示，Vc為輸出電壓，VD為續流二級管，L為濾波電感，C為濾波電容，R為負載電阻，iL為電感電流。

首先分析Buck變換器在可控開關管V開通和關斷兩種情況下的電路特性，其對應的工作模式分別用u=1和u=0表示。

圖1　Buck變換器的電路拓撲Fig.1　Circuit topology of Buck converter

1)當可控開關管V導通時，即u=1，續流二級管VD承受反向偏壓而截止，輸入直流電源E與電感L串聯，此時為蓄能階段。基于基爾霍夫電壓和電流定律，得到Buck變換器導通時的微分方程：

(1)

2)當u=0時，可控開關管V截止，續流二級管VD承受正向偏壓而導通，并與電感L和負載電阻R構成閉環電路，此時為續流階段。類似地可以得到Buck變換器關斷時的微分方程為：

(2)

聯合式(1)～式(2)，則Buck變換器在可控開關管V導通和關斷兩種工作模式下的統一微分方程模型為：

(3)

這里進一步考慮系統負載R未知的情況。假設Buck變換器的負載為純阻性負載，系統穩定運行時的負載額定值為R0，負載估計器設計如下

(4)

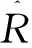
(5)

可見，Buck變換器的控制量u只能為1或0，其數學模型屬于控制受限的變結構控制系統。

2　Buck變換器的雙閉環終端滑模控制

下面對比給出圖1 Buck變換器的傳統單閉環線性滑模控制器和雙閉環終端滑模控制器的設計過程。

2.1傳統單閉環線性滑模控制

目前，Buck變換器的單閉環線性滑模控制方法通常選取電感電流或電容電壓作為控制變量來設計線性滑模控制器。這里以電感電流為例，給出其設計過程。

首先，設計線性滑模面

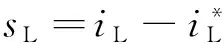
(6)

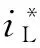
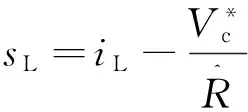
(7)

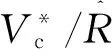
(8)

且同時應滿足基爾霍夫電壓定律，即有

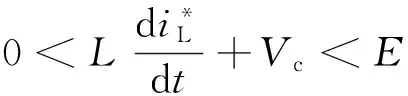
(9)

考慮到實際系統中開關管的開關頻率不能無限快，因此采用滯環調制對式(8)sign(.)進行修正

(10)

其中Δ>0為滯環調制的邊界層寬度。

基于以上線性滑模控制器的設計，這必然會存在兩方面突出問題：

1)由于僅以電感電流iL作為控制變量，無法對電容電壓Vc的收斂過程進行瞬時控制；

2)線性滑模的漸近收斂性導致系統收斂慢、穩態誤差大。

2.2雙閉環終端滑模控制

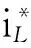
圖2　Buck變換器的雙閉環控制結構圖Fig.2　Double closed-loop control diagramof Buck converter

具體雙閉環控制器的設計過程如下。

步驟1：電容電壓終端滑模控制器的設計

(11)

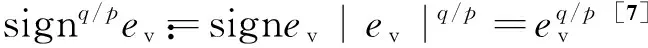
(12)

(13)

(14)

步驟2：電感電流線性滑模控制器的設計

(15)

這里直接選取線性滑模面

siL=eiL。

(16)

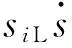
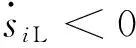
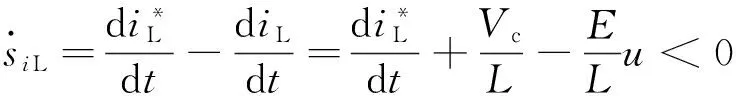
(17)

可見，此時可控開關管V的控制信號u=1；

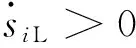
(18)

可見，此時可控開關管V的控制信號u=0。

綜合以上兩種情況，同樣可推導出保證Buck變換器穩定工作的約束條件如式(9)所示，繼而可得到對應的可控開關管V的切換控制為

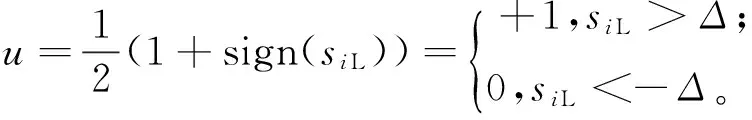
(19)

其中邊界層寬度Δ與如式(10)相同。

對比傳統單閉環線性滑模控制器，可見本文所提的雙閉環終端滑模控制方法的優點為

1)可同時實現對電容電壓和電感電流的瞬時控制，繼而使得Buck變換器電壓和電流均穩定在期望值；

2)利用具有有限時間收斂性的終端滑模控制方法可有效提高系統的響應速度和穩態精度。

3　仿真研究

傳統單閉環線性滑模控制器的設計參數Δ=0.01；雙閉環終端滑模控制器的設計參數β=900，q=3，p=5。

3.1額定工況

正常工作條件下采用雙閉環終端滑模控制方法和傳統單閉環線性滑模控制方法的對比仿真結果如圖3所示，其中圖3(a)為電容電壓(輸出電壓)的輸出波形，可見兩種方法都能實現無超調量控制，但采用雙閉環終端滑模控制方法的收斂時間約為5.3ms，穩態誤差為0.001 4V，而采用傳統線性滑模控制方法的收斂速度明顯慢，收斂時間約為15ms，穩態誤差為0.005 7V；圖3(b)為電感電流的輸出波形，可見雙閉環的控制結構較傳統的單閉環控制方式更能表現出電感電流的瞬時變化。基于以上顯著的仿真結果對比，可見雙閉環終端滑模控制方法的控制性能更好，收斂速度快且穩態精確度高。

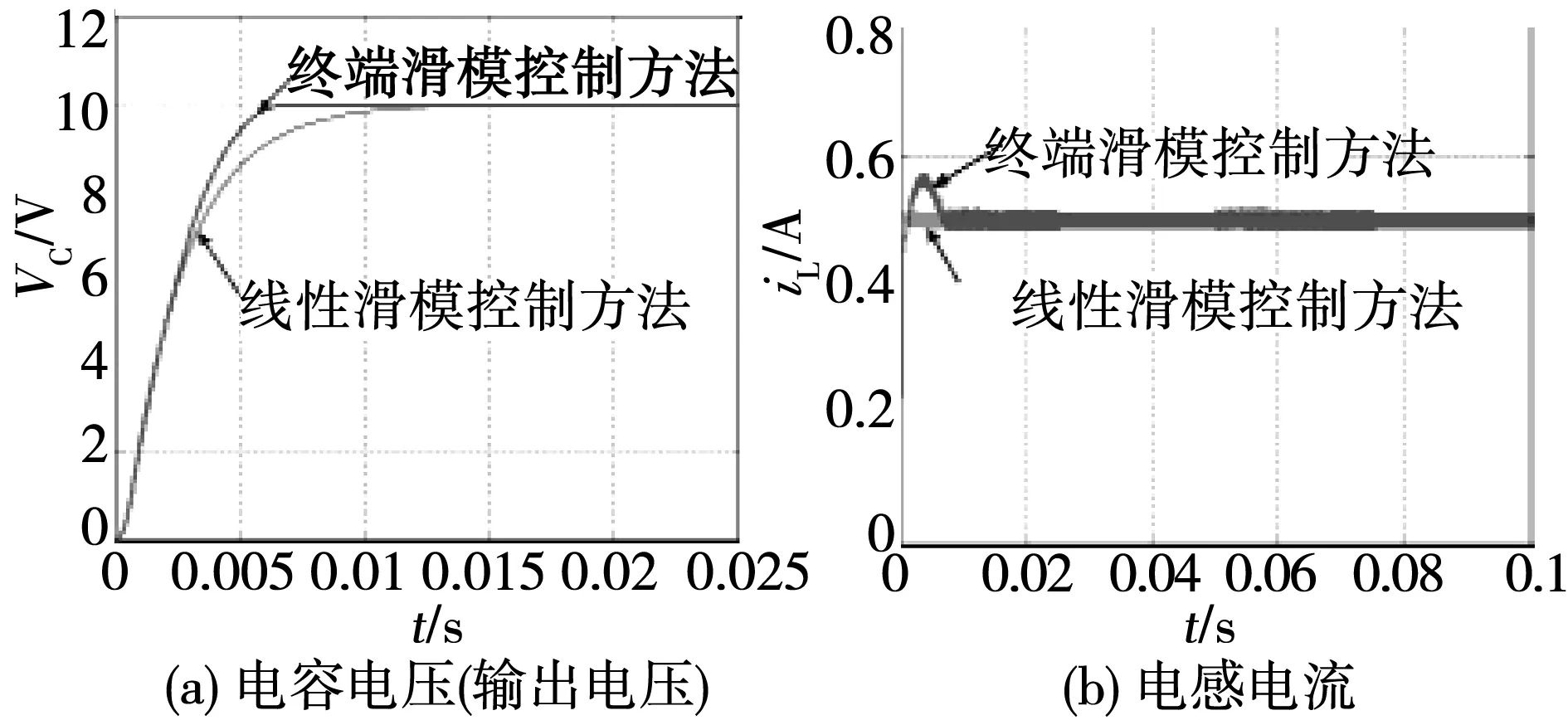
圖3　正常工作條件下的仿真結果Fig.3　Simulation results of normal condition

3.2直流輸入電壓存在擾動

假設從t=0.05s開始，直流輸入電壓E在20V與40V之間的大工作范圍內跳變，且每0.025s跳變一次。

圖4　直流輸入電壓存在擾動時的仿真結果對比Fig.4　Simulation comparisons in the case of DC input voltagedisturbance

3.3輸出參考電壓存在擾動

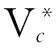
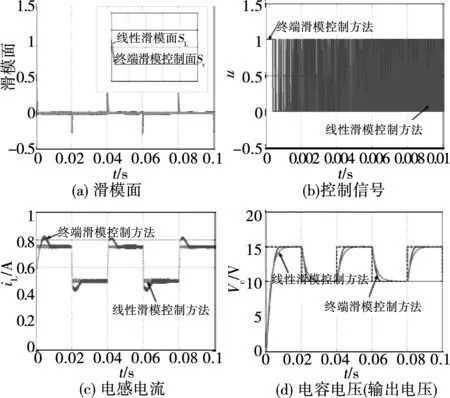
圖5　輸出參考電壓存在擾動時的仿真結果對比Fig.5　Simulation comparisons in the case of output reference voltage disturbance

控制方式電壓參考值/V輸出電壓穩態值/V穩態誤差/V單閉環線性滑模1010.0060.0061515.0040.004雙閉環終端滑模109.999-0.0011514.999-0.001

3.4負載電阻存在擾動

假設從t=0.02 s開始加入負載擾動，使得負載電阻R在20 Ω與5 Ω之間大負載調節范圍內跳變，且每0.025 s變化一次。

圖6為負載電阻R存在擾動時兩種方法的仿真結果對比，其中圖6(a)為采用式(4)負載估計器獲得的負載電阻觀測值，可見當實際負載電阻在20 Ω與5 Ω之間跳變時，由于負載估計器具有的過電流保護功能，使得其觀測值在20 Ω與10 Ω(1/2R0)之間跳變；圖6(b)～6(d)分別為兩種方法的滑模面、電感電流和電容電壓(輸出電壓)的輸出波形，與圖5輸出參考電壓存在擾動情況下的分析結果類似，同樣證明了所提雙閉環終端滑模控制方法響應速度快、控制精確度高的性能優勢。

圖6　負載電阻存在擾動時的仿真結果對比Fig.6　Simulation comparisons in the case ofload resistance

4　結　論

本文針對Buck變換器，提出一種新型的電容電壓/電感電流雙閉環終端滑模控制方法。在負載電阻未知情況下，基于基爾霍夫電壓和電流定律建立Buck變換器在開關導通和關斷兩種情況下的統一微分方程模型。與傳統單閉環線性滑模控制方法相比，本文采用雙閉環的控制結構來實時控制電容電

壓和電感電流的非線性瞬態變化，利用終端滑模控制方法的有限收斂和高穩態精度的特性來改進Buck變換器的控制性能和輸出電壓品質。多種情況下的仿真結果對比可證明所提控制方法的可行性和有效性。

[1]TAN S C,LAI Y M,TSE C K.General design issues of sliding-mode controllers in DC-DC converters [J]. IEEE Transactions on Industrial Electronics. 2008,55(3):1160-1174.

[2]王江, 王家軍, 王先來，等. 電力電子開關變換器的滑模控制[J]. 電機與控制學報,2000,4(3):188-192.

WANG Jiang, WANG Jia-jun, WANG Xian-lai，et al. Sliding mode control of power electronic converters[J].Electric Machines and Control,2000,4(3):188-192.

[3]倪雨, 許建平, 于海坤，等. 控制受限滑模控制Buck變換器設計[J]. 中國電機工程學報, 2010, 30(18): 26-32.

NI Yu, XU Jian-ping, YU Hai-kun et al. Design of sliding mode control Buck converter with bounded input[J].Proceedings of the CSEE, 2010, 30(18):26-32.

[4]張黎, 丘水生. Buck變換器的積分重構滑模控制 [J]. 電機與控制學報,2006,10(1): 93-96.

ZHANG Li, QIU Shui-sheng. Integral reconstructors sliding mode control for Buck converter[J].Electric Machines and Control, 2006,10(1): 93-96.

[5]FRIDMAN L,MORENO J,IRIARTE R.Sliding modes after the first decade of the 21stcentury [M]. Springer, 2011.

[6]MIDDLEBROOK R D, CUK S A. A general unified approach to modelling switching-converter power stages [C]//IEEE Power Electronics Specialists Conference, June 8-10,1976, Cleveland, OH: IEEE,1976: 18-34.

[7]YANG Liang, YANG Jianying. Nonsingular fast terminal sliding-mode control for nonlinear dynamical systems [J]. International Journal of Robust and Nonlinear Control. 2011,121(16): 1865-1879.

(編輯：賈志超)

Terminal sliding mode control for Buck converter with structure of voltage and current double closed loop

WANG Yan-min1,CAO Yu-qing2,XIA Hong-wei2

(1.School of Electrical Engineering and Automation,Harbin Institute of Technology,Harbin 150001, China;2. School of Astronautic,Harbin Institute of Technology,Harbin 150001,China)

In order to solve the problems of the traditional single closed-loop linear sliding mode (LSM) controller for Buck converter such as slower response speed and worse steady accuracy, a terminal sliding mode (TSM) control method with structure of voltage and current double closed loop is proposed. A load observer was designed to estimate the unknown resistance load as well as to realize the over-current protection. The unified differential equation model of Buck converter for the case of switching ON/OFF was established based on kirchhoff′s law and a TSM controller and LSM controller was designed for the outer capacitor voltage subsystem and inner inductor current subsystem respectively to guarantee the transient performance and expected DC voltage output in the finite time. Meanwhile, the unified stability condition of Buck converter for the case of switching ON/OFF was deduced by the existence condition of sliding mode control. Simulation comparisons with the traditional method validate the the efficiency of the design.

sliding mode control; terminal sliding mode control; Buck converter; double closed-loop control；finite-time convergence

2015-05-18

國家自然科學基金(51307035,61304108)；教育部博士點基金(20122302120012)；中國博士后基金(2013M541377)

王艷敏(1979—)，女，博士，講師，研究方向為滑模控制、電力電子變換與控制等；

曹雨晴(1993—)，女，碩士研究生，研究方向滑模控制、魯棒控制等；

王艷敏

10.15938/j.emc.2016.08.012

TM 46;TP 13

A

1007-449X(2016)08-0092-06

夏紅偉(1979—)，男，博士，副教授，研究方向為非線性控制、魯棒控制等。