基于EEMD和MFFOA-SVM滾動軸承故障診斷

何　青　褚東亮　毛新華

華北電力大學， 北京,102206

?

基于EEMD和MFFOA-SVM滾動軸承故障診斷

何青褚東亮毛新華

華北電力大學， 北京,102206

針對滾動軸承發生故障時，振動信號的時域和頻域特征都會發生變化的特點，提出了基于集合經驗模態分解(EEMD)、改進果蠅優化算法(MFFOA)和支持向量機(SVM)的滾動軸承故障診斷方法。該方法主要是利用EEMD方法對故障信號進行分解，并計算各IMF分量的均方根值和重心頻率，以此進行歸一化處理得到特征向量。為了提高診斷精度，采用果蠅優化算法優化SVM參數，建立MFFOA-SVM模型，然后對提取的特征向量進行訓練與測試，從而識別故障與否及發生點蝕故障的程度。利用該方法對實測信號進行分析與診斷,并與遺傳算法的優化結果進行對比，驗證了該方法的有效性，說明其具有良好的應用前景。

集合經驗模態分解；改進果蠅優化算法；支持向量機；滾動軸承；故障診斷

0　引言

滾動軸承是各種旋轉機械中應用最廣泛的一種通用部件，也是最容易損壞的部件之一，其運行狀態往往直接影響整臺機器的性能，一旦滾動軸承出現故障就會造成巨大的經濟損失，因此必須對其進行監測和診斷[1]。

對于傳統的故障診斷方法，通過時域或頻域分析對滾動軸承工作狀態進行精確診斷是比較困難的[2]。近年來，許多學者對滾動軸承故障診斷方法進行了研究。于德介等[3]首次闡述了內稟模態函數(intrinsic mode function，IMF)分量在機械故障診斷中的應用，將M距離函數和支持向量機(support vector machine，SVM)進行結合，實現了故障模式識別。雖然SVM能夠實現小樣本識別分類且克服了神經網絡局部極小值、結構和類型過分依賴于經驗等缺點，但是，SVM需要通過核參數將特征向量映射到高維空間，其核參數和懲罰參數選擇正確與否會影響到分類結果與精度。張濤等[4]將內稟模態特征能量法分別與SVM和神經網絡結合，將其應用于滾動軸承故障模式識別，結果表明，與 SVM 相結合的診斷識別率高于神經網絡的診斷識別率，但是對滾動軸承故障診斷識別率也僅為85%，主要是因為SVM分類器核參數的選擇依賴于經驗，常常得不到優化的核參數，導致識別率較低。

為了提高滾動軸承故障診斷的識別率，本文提出基于集合經驗模態分解(ensemble empirical mode decomposition，EEMD)和改進果蠅優化算法(modified fruit fly optimization algorithm，MFFOA)和支持向量機的滾動軸承故障診斷方法。利用EEMD分解故障信號，選擇IMF分量的均方根值和重心頻率作為特征向量；利用MFFOA對SVM分類器的核參數和懲罰參數進行優化；利用MFFOA-SVM模型對所提取的實測信號的特征向量進行訓練和測試，并將其分別與EEMD和MFFOA-SVM的診斷預測結果進行對比。

1　集合經驗模態分解

EEMD分解法是對原始經驗模態分解(empirical mode decomposition，EMD)[5-7]方法的重大改進。這種方法通過給信號加入極小幅度的白噪聲，利用白噪聲頻譜均衡分布的特點，用白噪聲來均衡噪聲的特性，較為理想地解決了模態混疊問題。具體步驟如下：

(1)在原始信號x(t)中多次加入等長度的正態分布的白噪聲ni(t)，即

xi(t)=x(t)+ni(t)

(1)

式中，xi(t)為第i次加入白噪聲后的信號。

(2)將添加了白噪聲的信號通過EMD算法進行分解，得到IMF分量Cij(t)和余項ri(t)，其中Cij(t)表示第i次加入白噪聲后分解所得的第j階IMF分量。

(3)利用不相關隨機序列的統計均值為零的原理，將各分量Cij(t)進行整體平均以抵消多次加入白噪聲對真實IMF分量的影響，得到最終EEMD分解結果，即

(2)

式中，Cj(t)為對原始信號進行EEMD分解得到的第j個IMF分量；N為添加白噪聲序列的數目。

此時EEMD分解的結果為

(3)

IMF分量Cj(t)(j=1,2,…)主要是信號從高到低不同頻段的成分信息，并且每個頻段包含著不同的頻率成分和能量，二者都會隨著振動信號x(t)的變化而改變。

2　果蠅算法與支持向量機

2.1果蠅算法原理

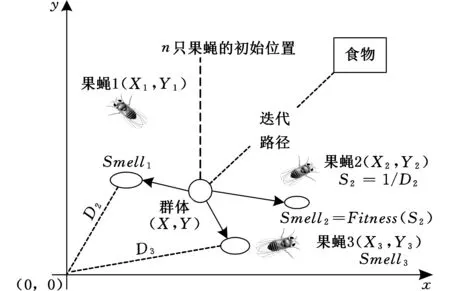
圖1　果蠅群體迭代搜索食物示意圖

根據果蠅的基本生理特性，仿真模擬其尋找食物的全過程，進而獲取具有良好全局性能的尋優方法[8]。對于果蠅來說，果蠅與食物之間的距離越遠，其味道就越小，否則反之。因此，果蠅搜尋食物的過程就是不斷地從味道小的地方到達味道更濃的地方的過程。如圖1所示，n只果蠅從果蠅群體初始位置沿著隨機方向飛出，然后所有果蠅再飛往味道濃度最高的果蠅位置，形成新的果蠅群體位置，再飛出，不斷反復循環，直到找到食物源位置為止[9-10]。

與其他演化算法基本相似，果蠅算法在尋優的過程中具有一定的隨機性，因此，該算法引入了同其他演化算法的適應函數的功能基本類似的味道濃度判定值和味道濃度判定函數，以便于準確地引導果蠅群體朝著正確的方向飛去，具體過程如圖2所示。

圖2　果蠅優化算法流程圖

依照果蠅覓食的習性可以將果蠅優化算法表述成以下幾個必要的步驟[11]：

(1)隨機初始化果蠅群體的坐標位置，得到初始坐標(X,Y) 。

(2)根據果蠅覓食行為的不同賦予其隨機方向和距離，具體的隨機距離按照初始坐標的位置來選擇：

Xi=X+Lr,Yi=Y+Lr

其中, Lr為在固定步長區間[-L,L]內隨機生成的步長值，可由Lr=L×rand(1,1)求得；L為果蠅個體利用嗅覺搜索的固定步長值。

(3)估計果蠅個體位置與坐標原點之間的距離Di,取距離的倒數作為果蠅味道濃度的判定值Si：

(4)

(4)將其果蠅味道濃度的判定值Si代入味道濃度的判定函數(或稱為適應度函數)Fitness, 求出果蠅個體位置的味道濃度Smelli，即Smelli=Fitness(Si)。

(5)根據果蠅初始味道濃度值，尋找該果蠅群體中味道濃度的極值(最優個體)bestSmell=max(Smelli) 或bestSmell=min(Smelli),同時保留其極值的迭代次數bestIndex。

(6)利用視覺尋找果蠅聚集味道濃度的最佳值，記錄果蠅此時的X、Y坐標和最優濃度bestSmell,并將其最佳味道濃度賦予Smellbest進行保留。果蠅的X、Y坐標為

(5)

(7)進入果蠅迭代尋優，重復執行步驟(2)～(5)，在保證果蠅迭代次數小于設定的最大迭代次數gmax前提下，判斷味道濃度是否優于前一次迭代味道濃度，若是,則執行步驟(6)。

2.2改進果蠅算法

在果蠅算法步驟(2)中，步長L設為固定值，即在每次覓食迭代中，果蠅個體以固定步長進行隨機搜索。在果蠅群體個數一定的情況下，若步長值過小，則果蠅個體的局部尋優能力較強，搜索空間較小，全局搜索能力較弱，果蠅個體容易陷入局部最優；反之，若步長值過大，則果蠅個體的搜索空間變大，全局搜索能力變強，但是局部尋優能力減弱?？梢?，在傳統果蠅算法中，如何正確地選擇步長參數會直接影響算法的執行效率。

因此，在運用果蠅算法解決實際問題時，為了避免全局搜索能力陷入局部最優，提出了改進果蠅優化算法MFFOA。具體改進部分如下:

(6)

式中，L0為初始步長值；Imax為最大覓食迭代次數；I為當前覓食迭代次數；L為遞減步長值。

當第1代果蠅覓食時，令L=L0，果蠅個體步長為最大值L0。隨后果蠅覓食迭代每增加1代，步長就減小L0/Imax，直到最后一代減到L0/Imax為止。

因此，MFFOA在迭代早期搜索步長最大，且搜索空間也大，全局尋優能力最強。隨著覓食迭代次數的不斷增加，該算法的局部搜索能力也在逐漸增強，能夠提高覓食早期全局最優解的概率,避免陷入局部最優，覓食末期能夠達到最大的搜索精度，從而實現全局搜索能力和局部尋優能力的平衡。

2.3支持向量機原理

統計學習理論[12]提出，把函數集構造為一個函數子集序列，使各個子集按照置信風險的大小排列；在每個子集中尋找最小經驗風險，通常它隨著子集復雜程度的增加而減小。折中考慮經驗風險和置信風險，使得實際風險最小，這就是結構風險最小化原則, 它改變了傳統的經驗風險最小化原則，在預測性能方面明顯優于神經網絡法[13-14]。

通過非線性映射的函數，得到滿足多維樣本輸入、一維樣本輸出原則的向量，將其作為輸入向量從原來的空間映射到高維特征空間H，并在該特征空間H內建立優化超平面，分類線方程如下[15-16]:

ω·x+b=0

(7)

式中，ω為權值矢量；x為輸入向量;b為閾值。

并且使得該超平面將兩類不同的樣本正確地分類，此外，還應使該超平面滿足如下的約束條件：

yi[ω·xi+b]≥1i=1,2,…,l

(8)

式中，l為支持向量的數目。

從而得到分類間隔最大的超平面，也就是最優分類面，如圖3所示。

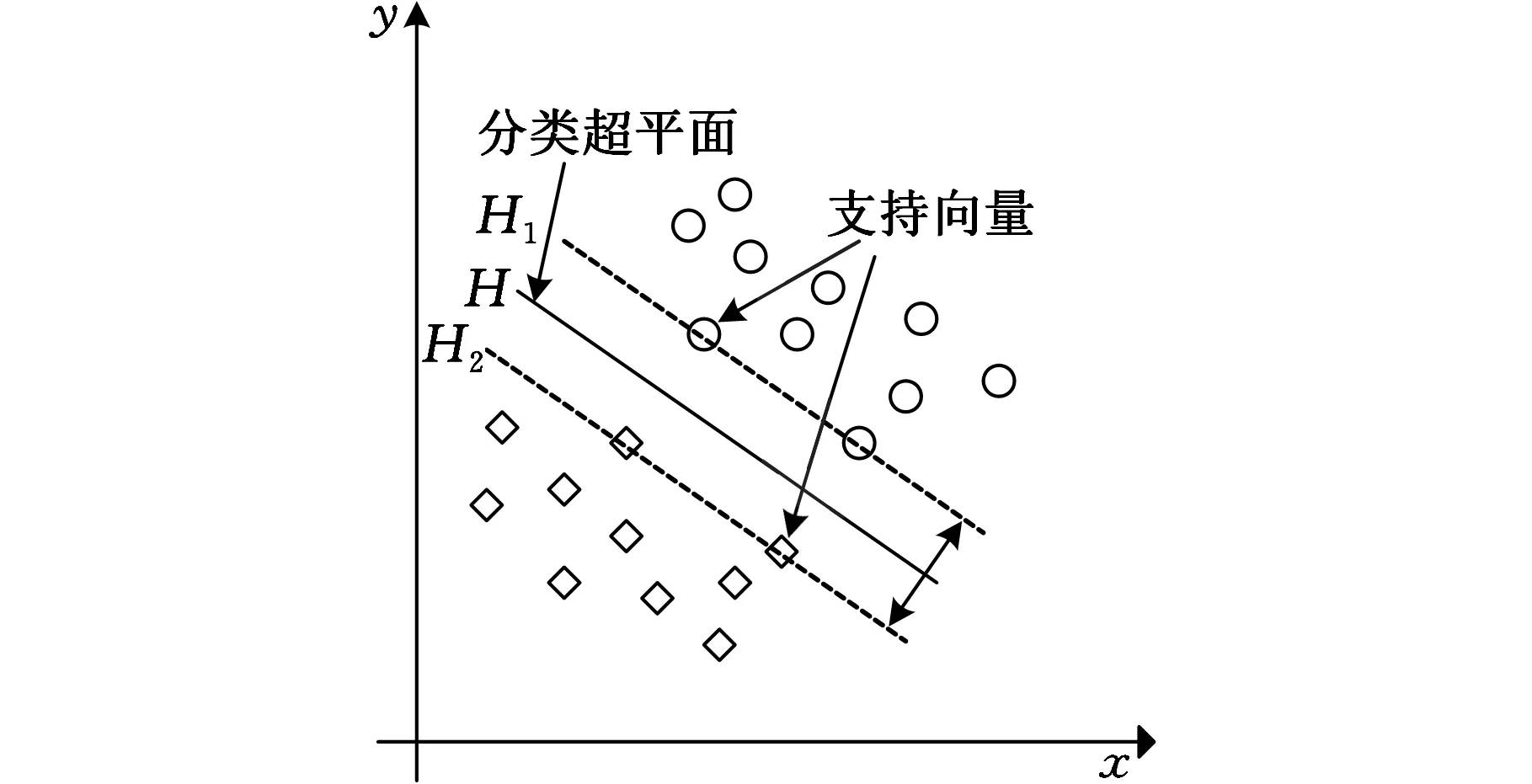
圖3　支持向量機的最優分類面

引入非負的松弛變量ξ、懲罰因子C、Lagrange乘子ai等參數，將約束優化問題轉化為如下問題：

(9)

根據Karush-Kuhn-Tucker的條件，優化系數滿足如下條件:

ai{yi[ω·xi+b]-1+ξi}=0

(10)

通過求解上述問題，最終可得到最優分類函數:

(11)

式中，σ(x,xi)為核函數。

適應度函數為

(12)

R(σ2,C)為訓練樣本的均方根誤差:

(13)

綜上所述，懲罰參數C和核函數參數σ是影響SVM分類器性能的關鍵參數，因此以(C，σ)作為尋優變量。

2.4MFFOA-SVM模型

通過MATLAB建立MFFOA-SVM模型，如圖4所示。

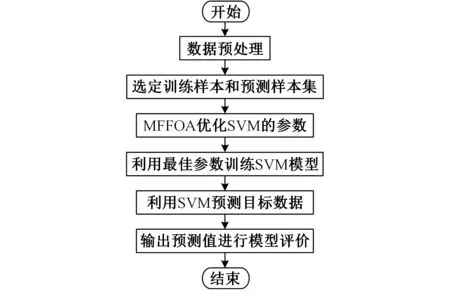
圖4　MFFOA-SVM訓練步驟

可以將MFFOA-SVM模型表述成以下幾個必要的步驟[17]：

(1)設定果蠅群體數目Spop，迭代次數gmax。由于優化參數有2個，所以初始果蠅位置時，X、Y應分別取2個隨機數，對每個果蠅覓食的飛行方向和距離賦值，得到初始坐標(X1，Y1), (X2，Y2)。估計果蠅個體位置與坐標原點之間的距離，得到果蠅味道濃度的判定值S1i、S2i。

(2)適當地選擇判定值的大小以確定懲罰因子C、核函數σ的取值范圍，C=mS1i，σ=nS2i。根據C、σ的取值范圍來調整m、n的取值大小。本文分別取C∈[0,1000]，σ∈[0,100]，為了讓S的定義域被限制在[0,10]之間，取m=100，n=10。

(3)對數據集特征值進行SVM 模型訓練，得到適應度函數f。

(4)果蠅濃度最高的位置即為f的最大值，保留該果蠅的坐標值，設為初始最佳坐標值。

(5)進入迭代尋優過程，保留最佳適應度函數和C、σ的參數值。此時應該注意，最佳的適應度對應多個C、σ的值，當C過大時，會造成誤差增大，因此保留最小的C以及對應的σ值。

3　實測信號診斷設計

為了驗證所提出方法的有效性，對來自美國Case Western Reserve University滾動軸承數據中心的實驗數據進行分析。該實驗測試平臺主要由驅動電機、轉矩傳感器、測力計和電子控制裝置組成，而驅動端和風扇端電機軸承分別包含型號為SKF6025-2RS和SKF6203-2RS的深溝球軸承，驅動端和風扇端軸承尺寸信息如表1所示[18]。

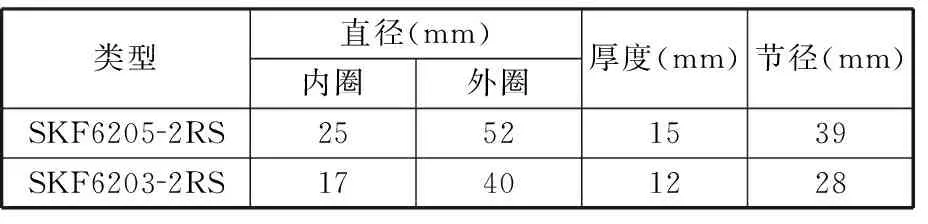
表1　滾動軸承參數

3.1信號數據說明

本文測試軸承為SKF6025-2RS深溝球軸承。對采樣頻率12 kHz、轉速1772 r/min時的故障數據進行分析。點蝕直徑不同，滾動軸承的故障程度不同，本文以點蝕直徑0.18 mm代表故障早期或者輕微故障，以點蝕直徑0.71 mm代表故障晚期或者嚴重故障。

由于故障特征參數不僅與故障類型有關，還與故障程度有關，也就是說同種故障不同程度，其特征參數規律也不相同，因此根據此特征，將測試信號分為8組，定義為類別標簽，每一組對應不同故障類型的不同程度。

這樣分類主要是考慮到誤差問題。如果某一個6組信號被識別成8組信號，則這個結果在8組分類中是錯誤的，但是從故障類型的角度來分析，這種“錯誤”是可以接受的，因為6、8組都屬于外圈故障，如表2所示。

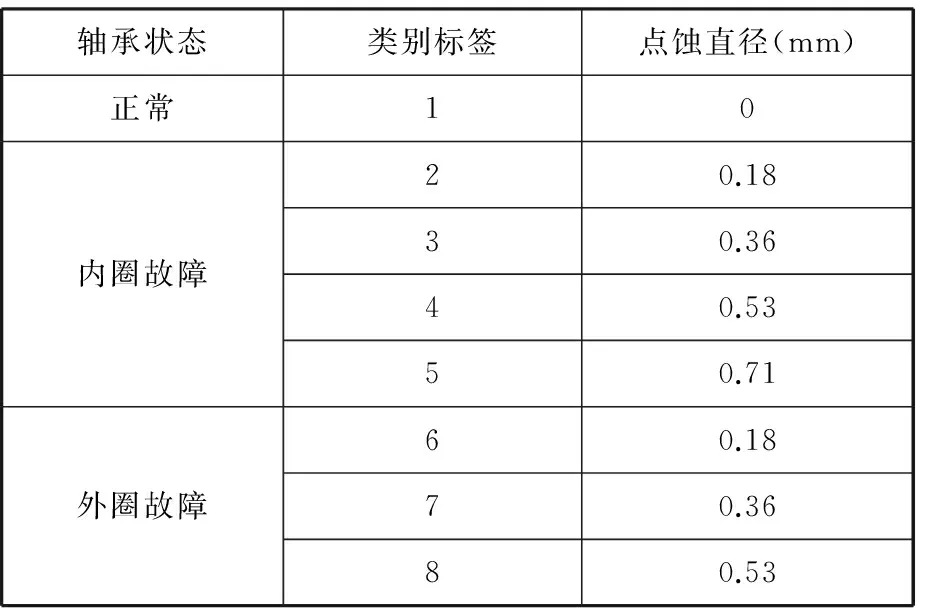
表2　滾動軸承數據分組

3.2故障診斷流程

具體故障診斷流程如圖5所示，即采用EEMD方法對滾動軸承振動信號進行歸一化處理，然后求出IMF分量的均方根值和重心頻率，組成故障特征向量，以MFFOA-SVM模型作為分類器來識別滾動軸承的工作狀態和故障類型[19-20]。

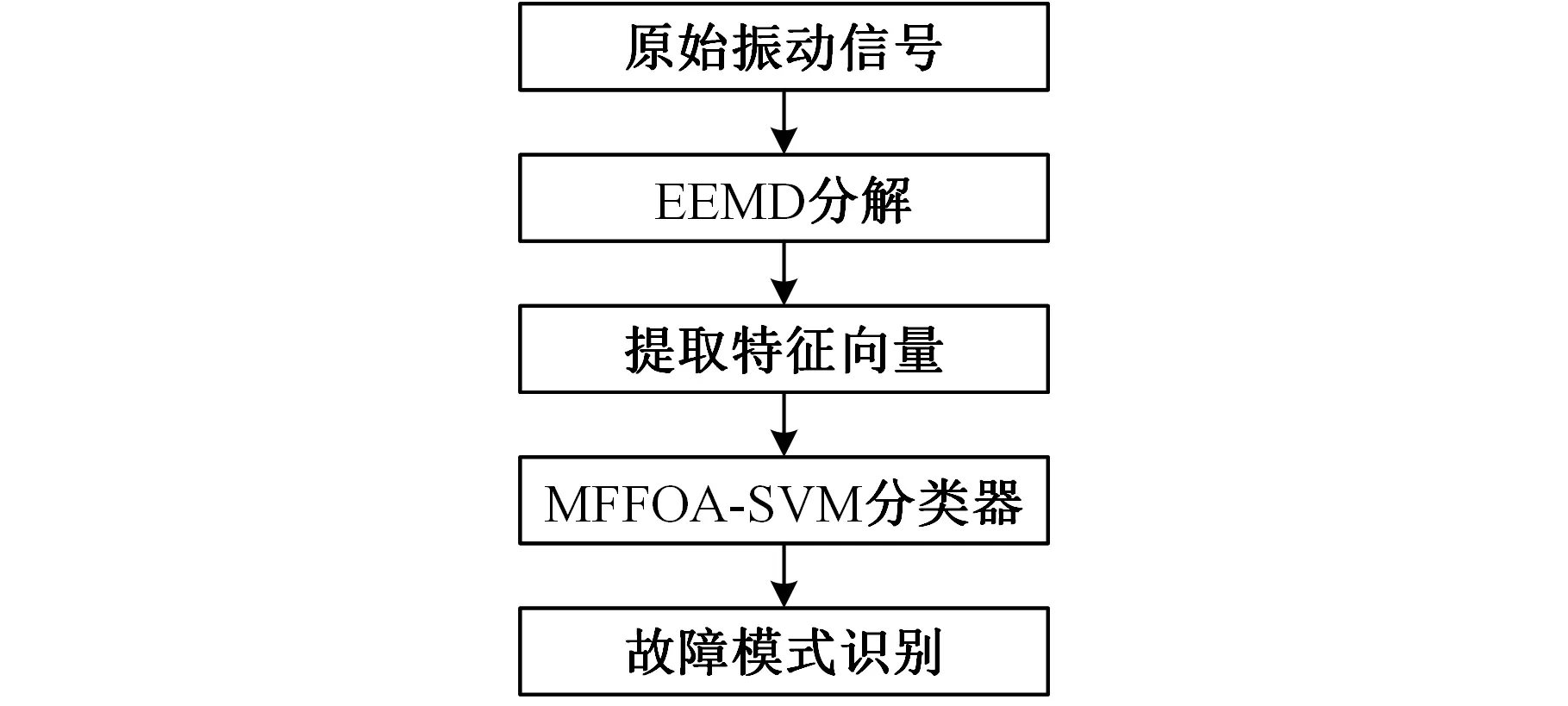
圖5　故障診斷流程圖

4　實測信號診斷分析

進行8組分類故障識別，其中正常取80組數據，內圈故障按照4種不同故障程度分別取40組數據，共160組數據；外圈故障按照3種不同故障程度分別取40組數據，共120組數據；總計360組數據。不同狀態的數據均等分為兩部分，一半輸入MFFOA-SVM作為訓練樣本進行學習，另一半作為測試樣本用來識別。

4.1時域-頻域多參數診斷

建立時域和頻域多參數特征向量，考慮到運算效率，從時域特征參數與頻域特征參數中分別提取均方根值和重心頻率，進行故障模式識別。

在識別前，對果蠅優化算法的參數進行設定，初始化果蠅群體設置區間為[0,1]，種群規模為20，迭代次數為100。MFFOA的搜尋結果發現，最佳的C=11.7769，最佳的σ=0.01。果蠅算法尋找最佳參數的進化迭代過程如圖6所示。

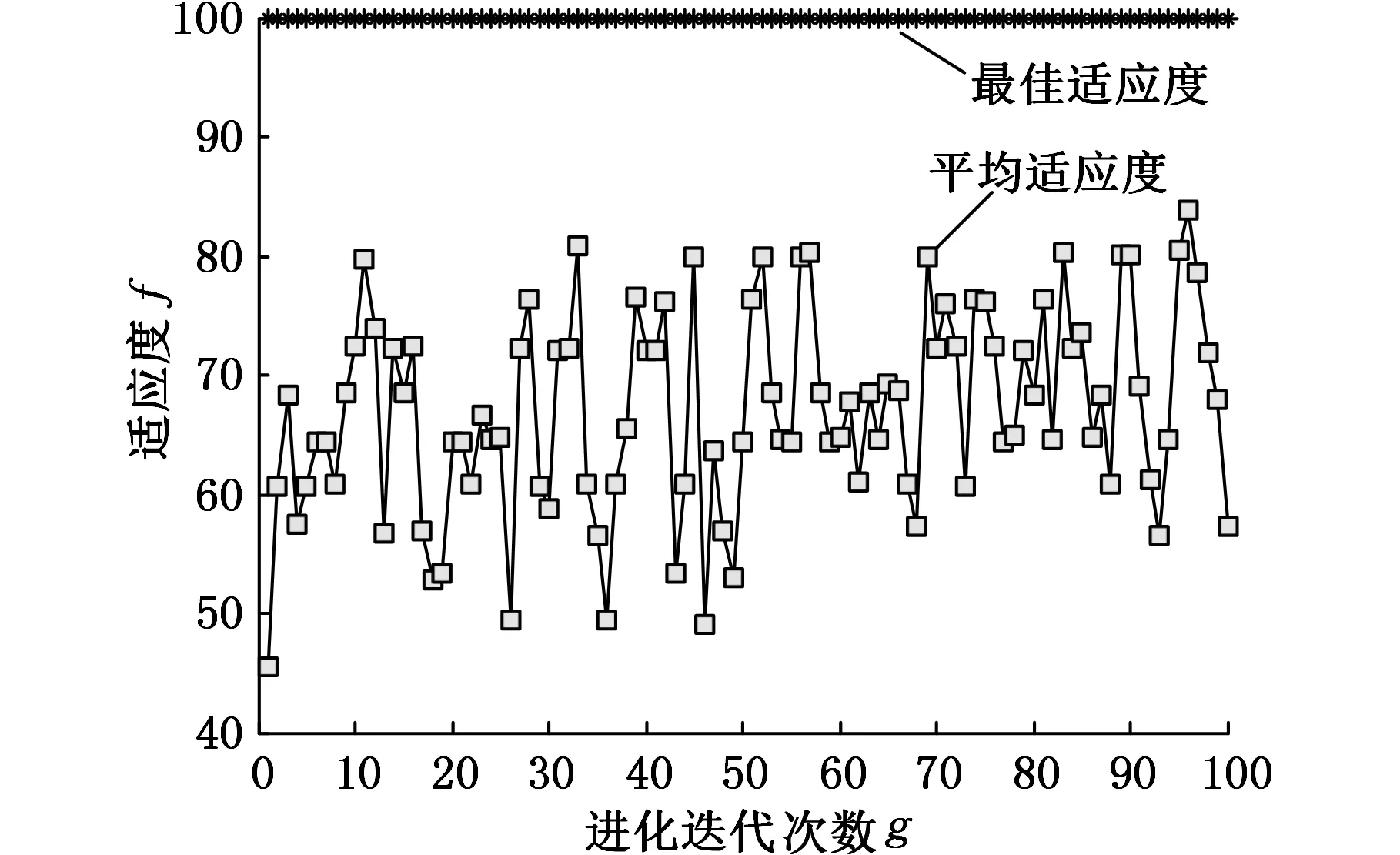
圖6　MFFOA尋找最佳參數的適應度曲線圖

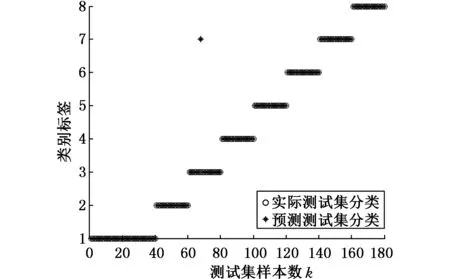
圖7　EEMD時域和頻域多參數的診斷分類圖(MFFOA-SVM)

圖8　EMD時域和頻域多參數的診斷分類圖(MFFOA-SVM)

通過MFFOA優化SVM最佳參數，可以得到EEMD和EMD時域和頻域多參數的診斷分類圖，見圖7和圖8。由圖7可知，內圈中有一個樣本被分錯，其余樣本的診斷結果完全正確；而圖8顯示，外圈和內圈分別有三個樣本和一個樣本被分錯，其余的全部診斷正確。經過對比，發現 EEMD時域和頻域多參數的診斷效果要優于EMD時域和頻域多參數的診斷效果。

4.2診斷結果分析

根據故障診斷流程，利用MFFOA優化SVM最佳參數，可以求出EEMD分解后的各IMF分量的均方根值與重心頻率兩種特征，前后排列作為特征向量進行診斷。具體分類準確率見表3。

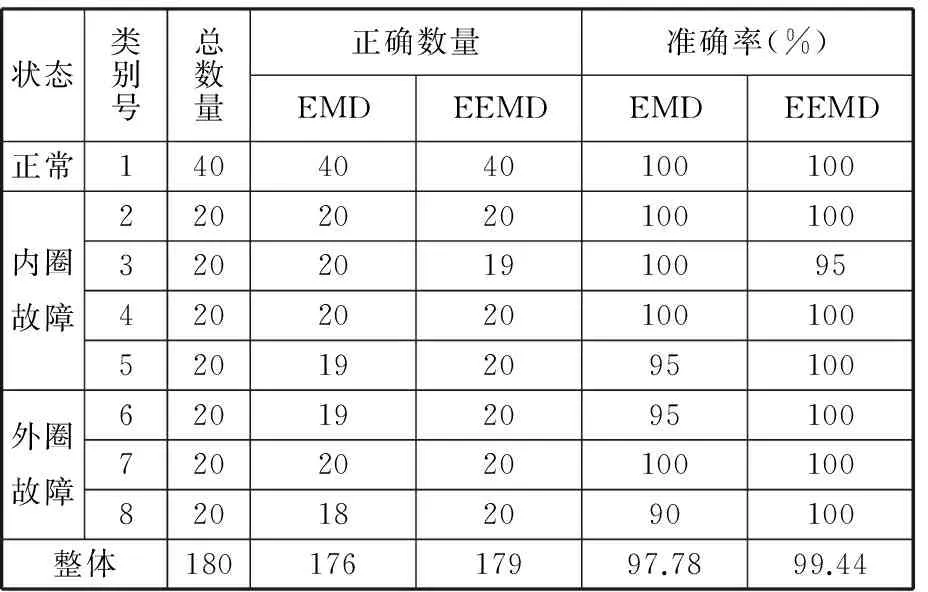
表3　時域和頻域多參數分類準確率(MFFOA-SVM)

由表3數據可知，EEMD和EMD時域頻域多參數的整體診斷準確率都在97%以上，說明該方法是有效的。而EEMD分類診斷準確率要比EMD分類診斷準確率高2%左右。

在內圈故障中， EEMD和EMD的故障診斷準確率是一致的，但是對點蝕故障程度的識別是不同的。EMD對點蝕直徑0.71 mm故障的診斷準確率是95%,而EEMD對點蝕直徑0.36 mm的診斷準確率是95%。

在外圈故障中，EEMD分解外圈故障的診斷準確率是100%,比EMD分解外圈故障的診斷準確率要高出很多。EMD分解對點蝕故障程度診斷準確率最低是90%。

對比遺傳算法(GA)優化SVM最佳參數，可以得到EEMD時域和頻域多參數的診斷分類圖，如圖9所示。由圖9可知，外圈中有兩個樣本出現故障，其余的診斷結果完全正確。同時，可以求出EEMD時域和頻域多參數的分類準確率，見表4。由表4可知，在內圈故障中，EEMD分解的診斷準確率為100%；在外圈故障中，EEMD對點蝕直徑為0.71 mm故障的識別率為90%。

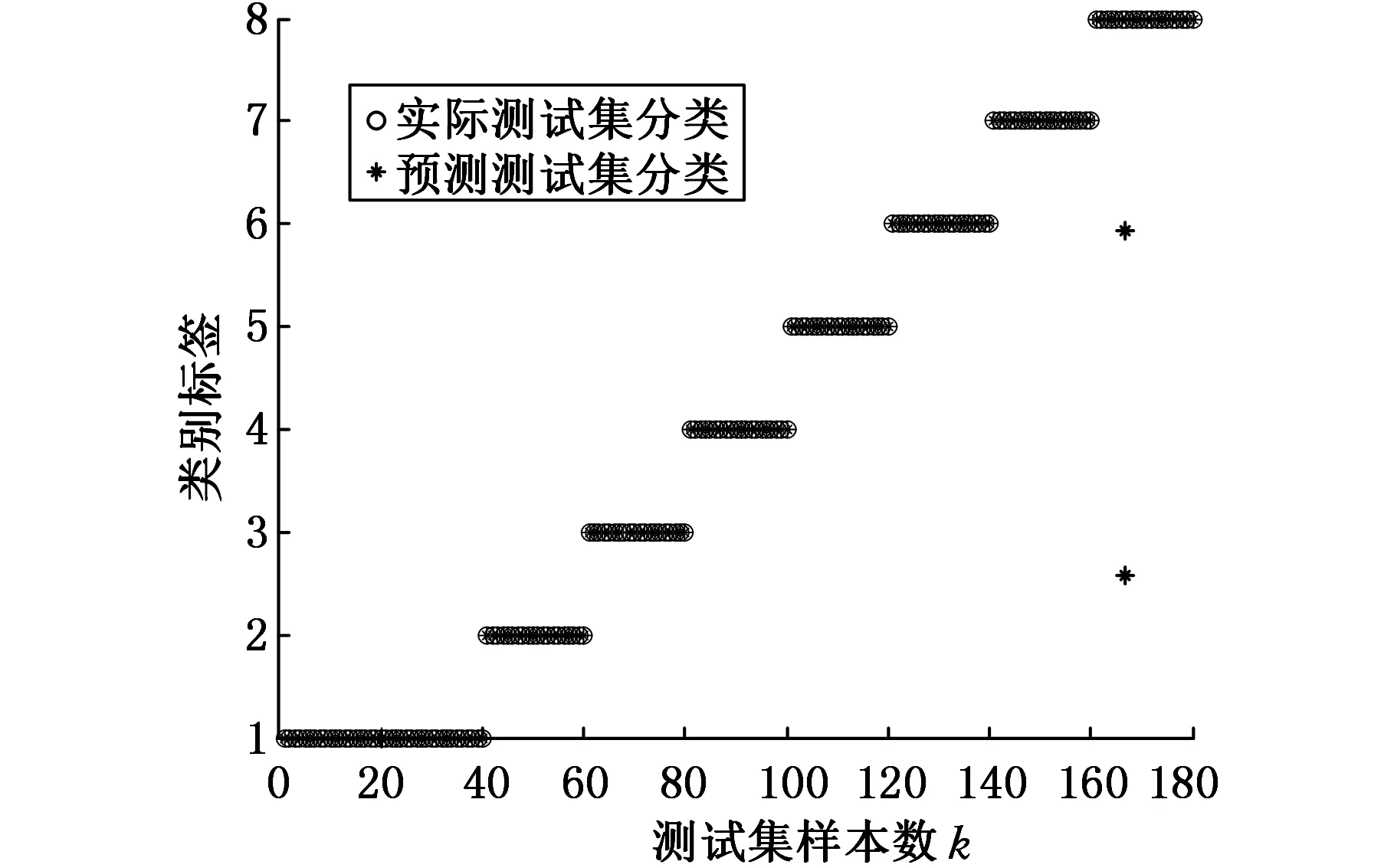
圖9　EEMD時域和頻域多參數的診斷分類圖(GA-SVM)

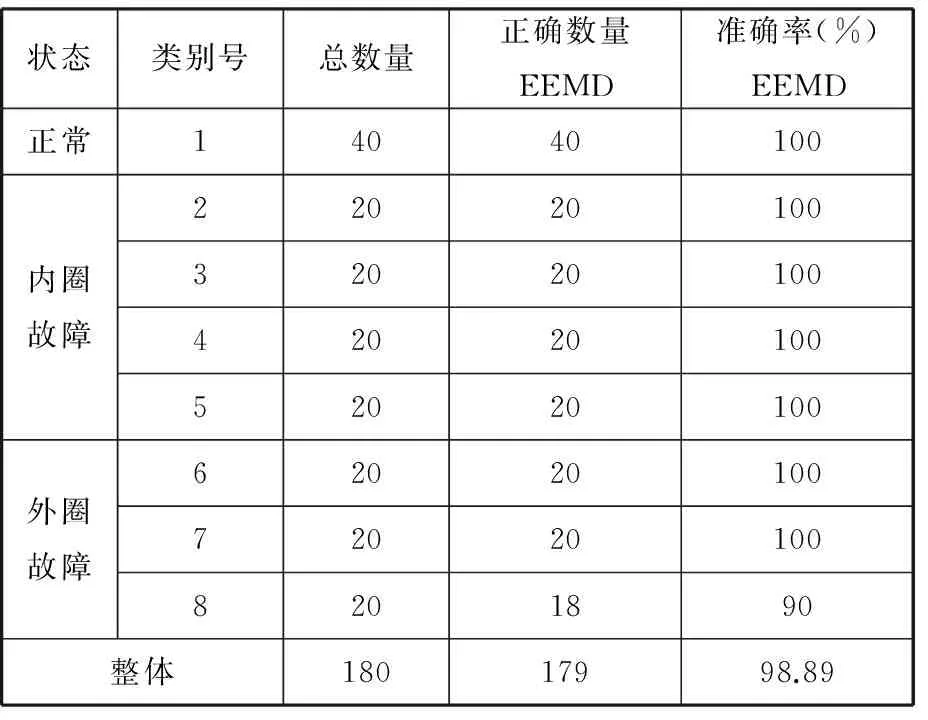
狀態類別號總數量正確數量EEMD準確率(%)EEMD正常14040100內圈故障22020100320201004202010052020100外圈故障62020100720201008201890整體18017998.89

基于訓練樣本數據，分別使用MFFOA和GA優化SVM回歸模型參數C和σ進行對比。表5所示為實測信號優化結果的定量對比，圖10為典型的實測信號分析中算法尋優進化曲線對比圖。由分析可見，MFFOA的尋優準確率要高于GA的尋優結果，且運行時間較短。

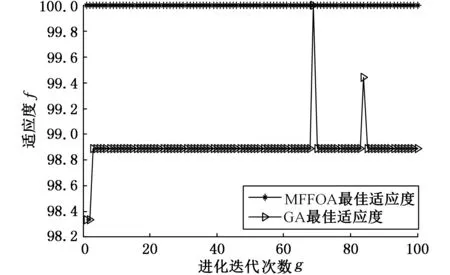
圖10　實測信號分析中算法適應度曲線

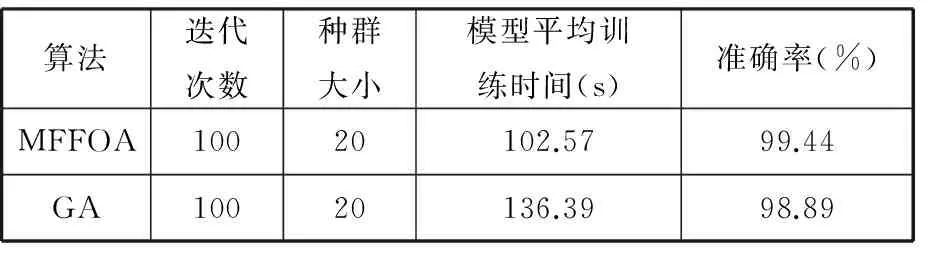
算法迭代次數種群大小模型平均訓練時間(s)準確率(%)MFFOA10020102.5799.44GA10020136.3998.89

5　結論

(1)使用具有全局搜索能力的MFFOA對SVM進行特征選擇與參數優化，可以提高SVM分類器的分類能力。

(2)基于EEMD和MFFOA-SVM的故障診斷準確率明顯高于EMD和MFFOA-SVM的故障診斷準確率，表明EEMD分解得到的IMF分量對軸承故障診斷更有效。

(3)與GA-SVM算法相比，基于EEMD和MFFOA-SVM模型的軸承故障診斷方法具有更加準確的分類效果和更高的診斷精度，該方法也可以應用于其他機械零部件的故障診斷。

[1]丁康, 孔正國. 振動調幅調頻信號的調制邊頻帶分析及其解調方法[J]. 振動與沖擊, 2006, 24(6): 9-12.

DingKang,KongZhengguo.ModulationVibrationAmplitudeModulationFrequencyModulationSignalSidebandAnalysisandDemodulationMethod[J].Vibration&Shock, 2006, 24(6): 9-12.

[2]TandonN,ChoudhuryA.AReviewofVibrationandAcousticMeasurementMethodsfortheDetectionofDefectsinRollingElementBearings[J].TribologyInternational, 1999, 32: 469-480.

[3]于德介, 程軍圣, 楊宇. 機械故障診斷的Hilbert-Huang變換方法[M]. 北京: 科學出版社, 2006.

[4]張 濤, 陸森林, 周海超, 等. 內稟模態特征能量法在滾動軸承故障模式識別中的應用[J]. 噪聲與振動控制, 2011, 31(3): 125-128.

ZhangTao,LuSenlin,ZhouHaichao,etal.ApplicationofIntrinsicModeFunctionFeatureEnergyMethodinFaultPatternRecognitionofRollingBearing[J].NoiseandVibrationControl, 2011, 31(3): 125-128.

[5]HuangE,ShenZheng,LongSR,etal.TheEmpiricalModeDecompositionandtheHilbertSpectrumforNonlinearandNon-stationaryTimeSeriesAnalysis[J].Proc.R.Soc.Lond.A, 1998, 454(12): 903-995.

[6]張俊紅, 李林潔, 馬文朋，等.EMD-ICA聯合降噪在滾動軸承故障診斷中的應用[J]. 中國機械工程, 2013, 24(11): 1468-1472.

ZhangJunhong,LiLinjie,MaWenpeng,etal.ApplicationofEMD-ICAtoFaultDiagnosisofRollingBearing[J].ChinaMechanicalEngineering, 2013, 24(11): 1468-1472.

[7]孟宗,李姍姍. 基于小波半軟閾值和EMD的旋轉機械故障診斷[J]. 中國機械工程,2013,24(10):1279-1283.

MengZong,LiShanshan.ResearchonFaultDiagnosisforRotatingMachineryBasedonSemi-softWaveletThresholdandEMD[J].ChinaMechanicalEngineering, 2013, 24(10): 1279-1283.

[8]潘文超. 果蠅最佳佳演化算法[M]. 臺北: 滄海書局, 2011.

[9]LiH,GuoS,ZhaoH,etal.AnnualElectricLoadForecastingbyaLeastSquaresSupportVectorMachinewithaFruitFlyOptimizationAlgorithm[J].Energies, 2012,5(11): 4430-4445.

[10]LiHZ,GuoS,LiCJ,etal.AHybridAnnualPowerLoadForecastingModelBasedonGeneralizedRegressionNeuralNetworkwithFruitFlyOptimizationAlgorithm[J].Knowledge-BasedSystems, 2013, 37, 378-387.

[11]牛培峰, 麻紅波, 李國強, 等. 基于支持向量機和果蠅優化算法的循環流化床鍋爐NOx排放特性研究[J]. 動力工程學報, 2013, 33(4): 267-271.

NiuPeifeng,MaHongbo,LiGuogiang,etal.StudyonNoxEmissionfromCFBBoilersBasedonSupportVectorMachineandFruitFlyOptimizationAlgorithm[J].JournalofChineseSocietyofPowerEngineering, 2013, 33(4): 267-271.

[12]章永來, 史海波, 周曉峰, 等. 基于統計學習理論的支持向量機預測模型[J]. 統計與決策, 2014(5): 72-74.

ZhangYonglai,ShiHaibo,ZhouXiaofeng,etal.SupportVectorMachinePredictionModelBasedonStatisticalLearningTheory[J].StatisticsandDecision, 2014(5): 72-74.

[13]楊金芳, 翟永杰, 王東風, 等. 基于支持向量回歸的時間序列預測[J]. 中國電機工程學報, 2005, 25(17): 110-114.

YangJinfang,ZhaiYongjie,WangDongfeng,etal.TimeSeriesPredictionBasedonSupportVectorRegression[J].ProceedingsoftheCSEE, 2005, 25(17): 110-114．

[14]謝宏, 魏江平, 劉鶴立. 短期負荷預測中支持向量機模型的參數選取和優化方法[J]. 中國電機工程學報, 2006, 26(22): 17-22.

XieHong,WeiJiangping,LiuHeli.ParameterSelectionandOptimizationMethodofSVMModelforShort-termLoadForecasting[J].ProceedingsoftheCSEE, 2006, 26(22): 17-22.

[15]丁世飛, 齊丙娟, 譚紅艷. 支持向量機理論與算法研究綜述[J]. 電子科技大學學報, 2011(1): 2-10.

DingShifei,QiBingjuan,TanHongyan.AnOverviewonTheoryandAlgorithmofSupportVectorMachines[J].JournalofUniversityofElectronicScienceandTechnology, 2011(1): 2-10.

[16]葉林, 劉鵬. 基于經驗模態分解和支持向量機的短期風電功率組合預測模型[J]. 中國電機工程學報, 2011, 31(31): 102-108.

YeLin,LiuPeng.CombinedModelBasedonEMD-SVMforShort-termWindPowerPrediction[J].ProceedingsoftheCSEE, 2011, 31(31): 102-108.

[17]ZhangJ,WangR,LiJ,etal.FruitFlyOptimizationBasedLeastSquareSupportVectorRegressionforBlindImageRestoration[C]//InternationalSymposiumonOptoelectronicTechnologyandApplication2014.Beijing:InternationalSocietyforOpticsandPhotonics, 2014: 93011W-93011W-8.

[18]LoparoKA.TheCaseWesternReserveUniversityBearingDataCenter[EB/OL]. [2012-11-15].http: //csegroups.ase.edu/hearingdatacenter/pages/download-data-file.

[19]RenY,SuganthanPN,SrikanthN.AComparativeStudyofEmpiricalModeDecomposition-basedShort-termWindSpeedForecastingMethods[J].SustainableEnergy, 2015, 6(1): 236-244.

[20]YangCY,WuTY.DiagnosticsofGearDeteriorationUsingEEMDApproachandPCAProcess[J].Measurement, 2015, 61: 75-87.

(編輯蘇衛國)

Study on Rolling Bearing Fault Diagnosis Based on EEMD and MFFOA-SVM

He QingChu DongliangMao Xinhua

North China Electric Power University, Beijing， 102206

Both of the time domain and frequency domain of the vibration signals would be changed when rolling bearing faults occured. A rolling bearing fault diagnosis method was proposed based on EEMD, MFFOA and SVM. EEMD was used to decompose the fault signals, and to calculate the root mean square value and frequency of the center of gravity, achieving the normalization processing feature vector. In order to improve the classification accuracy rate, a MFFOA-SVM model was built, and then the feature values were extracted for training and testing, so that it might recognize the faults or not and the degree of pitting corrosion failures. The actual signals were analyzed and diagnosed, and compared with genetic algorithm optimization results, it proves the validity of the method, and the improved method has a good prospect for its applications in rolling bearing diagnosis.

ensemble empirical mode decomposition(EEMD); modified fruit fly optimization algorithm(MFFOA); support vector machine(SVM); rolling bearing; fault diagnosis

2015-07-13

中央高校基本科研業務費專項資金資助項目(2014XS25，2014MS17)

TH113.2;TB533

10.3969/j.issn.1004-132X.2016.09.009

何青，男，1962年生。華北電力大學能源動力與機械工程學院教授、博士研究生導師。研究方向為振動工程與測試技術、狀態監測與故障診斷。褚東亮，男，1984年生。華北電力大學能源動力與機械工程學院博士研究生。毛新華，男，1975年生。華北電力大學能源動力與機械工程學院博士研究生。